Bayesian Influence Functions for Hessian-Free Data Attribution

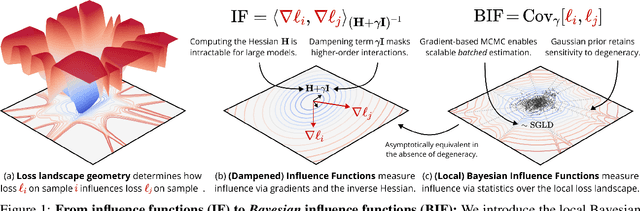
Classical influence functions face significant challenges when applied to deep neural networks, primarily due to non-invertible Hessians and high-dimensional parameter spaces. We propose the local Bayesian influence function (BIF), an extension of classical influence functions that replaces Hessian inversion with loss landscape statistics that can be estimated via stochastic-gradient MCMC sampling. This Hessian-free approach captures higher-order interactions among parameters and scales efficiently to neural networks with billions of parameters. We demonstrate state-of-the-art results on predicting retraining experiments.

Unifying and Verifying Mechanistic Interpretations: A Case Study with Group Operations

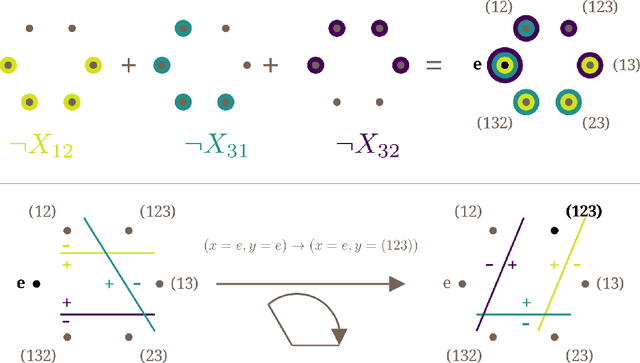
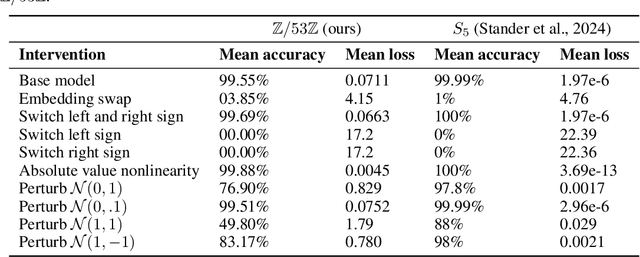
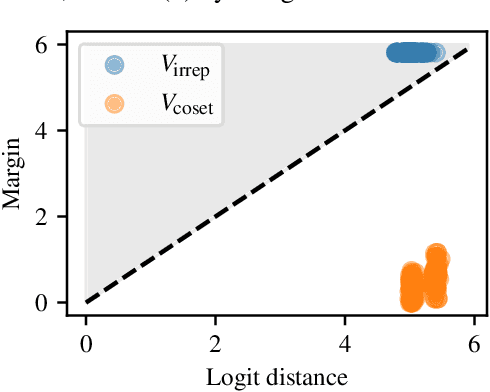
A recent line of work in mechanistic interpretability has focused on reverse-engineering the computation performed by neural networks trained on the binary operation of finite groups. We investigate the internals of one-hidden-layer neural networks trained on this task, revealing previously unidentified structure and producing a more complete description of such models that unifies the explanations of previous works. Notably, these models approximate equivariance in each input argument. We verify that our explanation applies to a large fraction of networks trained on this task by translating it into a compact proof of model performance, a quantitative evaluation of model understanding. In particular, our explanation yields a guarantee of model accuracy that runs in 30% the time of brute force and gives a >=95% accuracy bound for 45% of the models we trained. We were unable to obtain nontrivial non-vacuous accuracy bounds using only explanations from previous works.

Do language models plan ahead for future tokens?

Do transformers "think ahead" during inference at a given position? It is known transformers prepare information in the hidden states of the forward pass at $t$ that is then used in future forward passes $t+\tau$. We posit two explanations for this phenomenon: pre-caching, in which off-diagonal gradient terms present in training result in the model computing features at $t$ irrelevant to the present inference task but useful for the future, and breadcrumbs, in which features most relevant to time step $t$ are already the same as those that would most benefit inference at time $t+\tau$. We test these hypotheses by training language models without propagating gradients to past timesteps, a scheme we formalize as myopic training. In a synthetic data setting, we find clear evidence for pre-caching. In the autoregressive language modeling setting, our experiments are more suggestive of the breadcrumbs hypothesis.

Learning Deterministic Finite Automata from Confidence Oracles

We discuss the problem of learning a deterministic finite automaton (DFA) from a confidence oracle. That is, we are given access to an oracle $Q$ with incomplete knowledge of some target language $L$ over an alphabet $\Sigma$; the oracle maps a string $x\in\Sigma^*$ to a score in the interval $[-1,1]$ indicating its confidence that the string is in the language. The interpretation is that the sign of the score signifies whether $x\in L$, while the magnitude $|Q(x)|$ represents the oracle's confidence. Our goal is to learn a DFA representation of the oracle that preserves the information that it is confident in. The learned DFA should closely match the oracle wherever it is highly confident, but it need not do this when the oracle is less sure of itself.

Generating Semantic Adversarial Examples with Differentiable Rendering

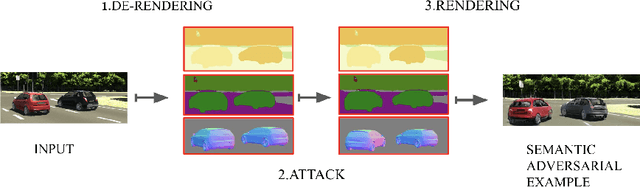
Machine learning (ML) algorithms, especially deep neural networks, have demonstrated success in several domains. However, several types of attacks have raised concerns about deploying ML in safety-critical domains, such as autonomous driving and security. An attacker perturbs a data point slightly in the concrete feature space (e.g., pixel space) and causes the ML algorithm to produce incorrect output (e.g. a perturbed stop sign is classified as a yield sign). These perturbed data points are called adversarial examples, and there are numerous algorithms in the literature for constructing adversarial examples and defending against them. In this paper we explore semantic adversarial examples (SAEs) where an attacker creates perturbations in the semantic space representing the environment that produces input for the ML model. For example, an attacker can change the background of the image to be cloudier to cause misclassification. We present an algorithm for constructing SAEs that uses recent advances in differential rendering and inverse graphics.