Unifying and Verifying Mechanistic Interpretations: A Case Study with Group Operations
Paper and Code
Oct 09, 2024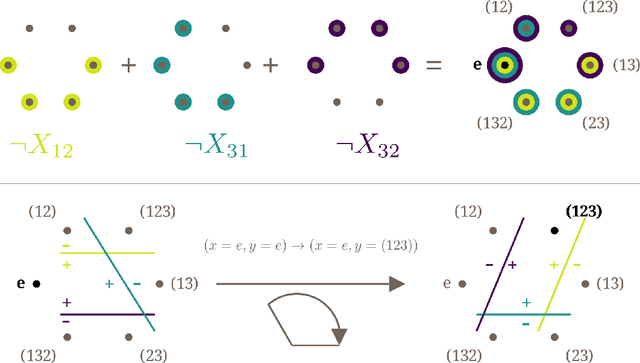
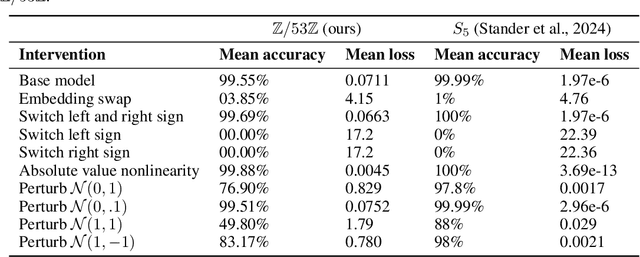
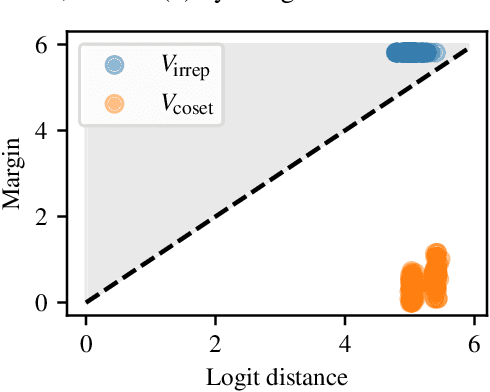

A recent line of work in mechanistic interpretability has focused on reverse-engineering the computation performed by neural networks trained on the binary operation of finite groups. We investigate the internals of one-hidden-layer neural networks trained on this task, revealing previously unidentified structure and producing a more complete description of such models that unifies the explanations of previous works. Notably, these models approximate equivariance in each input argument. We verify that our explanation applies to a large fraction of networks trained on this task by translating it into a compact proof of model performance, a quantitative evaluation of model understanding. In particular, our explanation yields a guarantee of model accuracy that runs in 30% the time of brute force and gives a >=95% accuracy bound for 45% of the models we trained. We were unable to obtain nontrivial non-vacuous accuracy bounds using only explanations from previous works.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge