On Need for Topology-Aware Generative Models for Manifold-Based Defenses

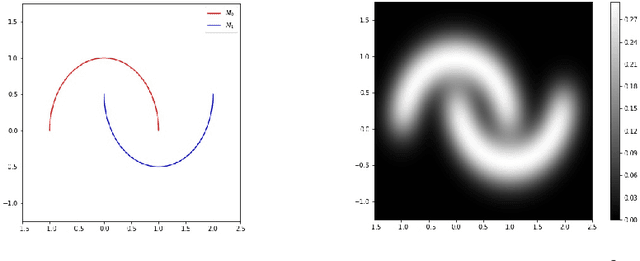
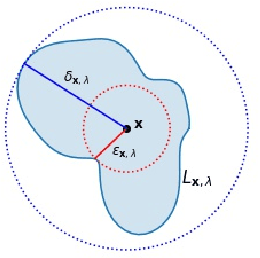
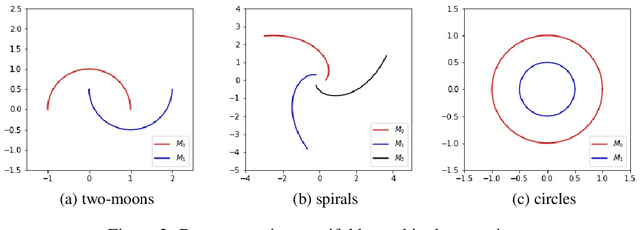
ML algorithms or models, especially deep neural networks (DNNs), have shown significant promise in several areas. However, recently researchers have demonstrated that ML algorithms, especially DNNs, are vulnerable to adversarial examples (slightly perturbed samples that cause mis-classification). Existence of adversarial examples has hindered deployment of ML algorithms in safety-critical sectors, such as security. Several defenses for adversarial examples exist in the literature. One of the important classes of defenses are manifold-based defenses, where a sample is "pulled back" into the data manifold before classifying. These defenses rely on the manifold assumption (data lie in a manifold of lower dimension than the input space). These defenses use a generative model to approximate the input distribution. This paper asks the following question: do the generative models used in manifold-based defenses need to be topology-aware? Our paper suggests the answer is yes. We provide theoretical and empirical evidence to support our claim.

Generating Semantic Adversarial Examples with Differentiable Rendering

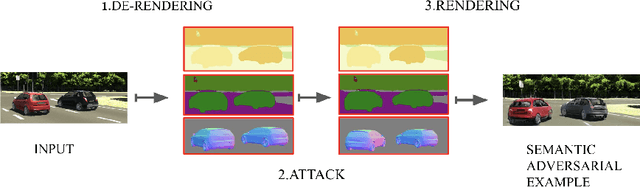
Machine learning (ML) algorithms, especially deep neural networks, have demonstrated success in several domains. However, several types of attacks have raised concerns about deploying ML in safety-critical domains, such as autonomous driving and security. An attacker perturbs a data point slightly in the concrete feature space (e.g., pixel space) and causes the ML algorithm to produce incorrect output (e.g. a perturbed stop sign is classified as a yield sign). These perturbed data points are called adversarial examples, and there are numerous algorithms in the literature for constructing adversarial examples and defending against them. In this paper we explore semantic adversarial examples (SAEs) where an attacker creates perturbations in the semantic space representing the environment that produces input for the ML model. For example, an attacker can change the background of the image to be cloudier to cause misclassification. We present an algorithm for constructing SAEs that uses recent advances in differential rendering and inverse graphics.

Reinforcing Adversarial Robustness using Model Confidence Induced by Adversarial Training

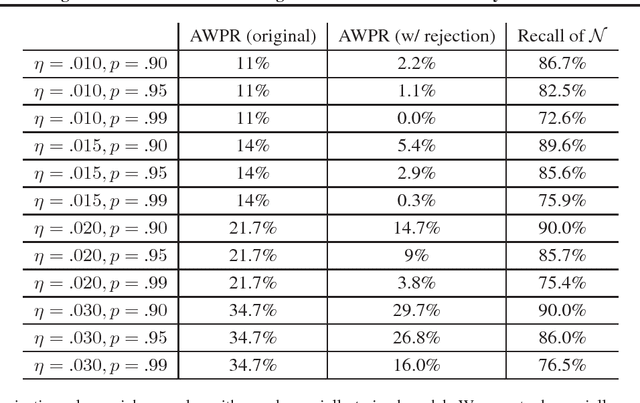
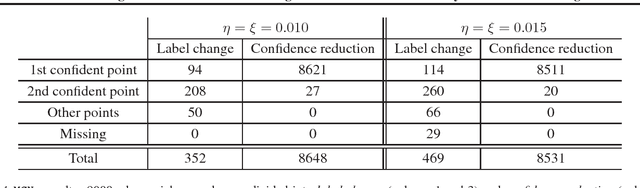
In this paper we study leveraging confidence information induced by adversarial training to reinforce adversarial robustness of a given adversarially trained model. A natural measure of confidence is $\|F({\bf x})\|_\infty$ (i.e. how confident $F$ is about its prediction?). We start by analyzing an adversarial training formulation proposed by Madry et al.. We demonstrate that, under a variety of instantiations, an only somewhat good solution to their objective induces confidence to be a discriminator, which can distinguish between right and wrong model predictions in a neighborhood of a point sampled from the underlying distribution. Based on this, we propose Highly Confident Near Neighbor (${\tt HCNN}$), a framework that combines confidence information and nearest neighbor search, to reinforce adversarial robustness of a base model. We give algorithms in this framework and perform a detailed empirical study. We report encouraging experimental results that support our analysis, and also discuss problems we observed with existing adversarial training.