Reinforcing Adversarial Robustness using Model Confidence Induced by Adversarial Training
Paper and Code
Jun 08, 2018
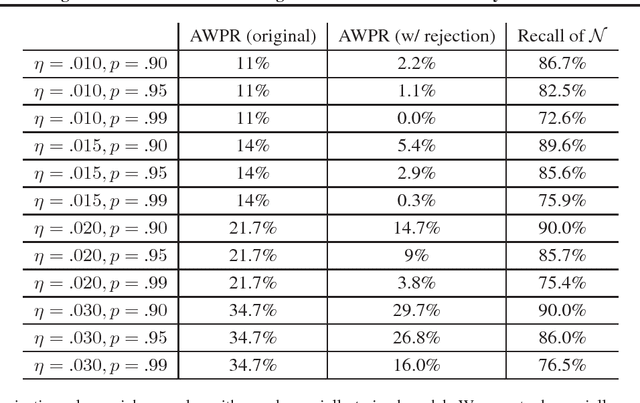

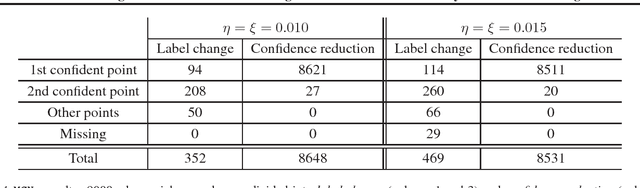
In this paper we study leveraging confidence information induced by adversarial training to reinforce adversarial robustness of a given adversarially trained model. A natural measure of confidence is $\|F({\bf x})\|_\infty$ (i.e. how confident $F$ is about its prediction?). We start by analyzing an adversarial training formulation proposed by Madry et al.. We demonstrate that, under a variety of instantiations, an only somewhat good solution to their objective induces confidence to be a discriminator, which can distinguish between right and wrong model predictions in a neighborhood of a point sampled from the underlying distribution. Based on this, we propose Highly Confident Near Neighbor (${\tt HCNN}$), a framework that combines confidence information and nearest neighbor search, to reinforce adversarial robustness of a base model. We give algorithms in this framework and perform a detailed empirical study. We report encouraging experimental results that support our analysis, and also discuss problems we observed with existing adversarial training.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge