NeuroComb: Improving SAT Solving with Graph Neural Networks

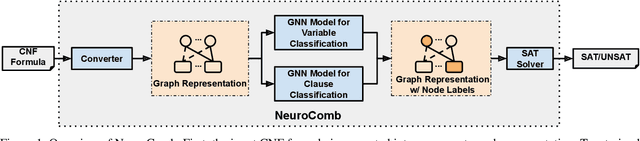
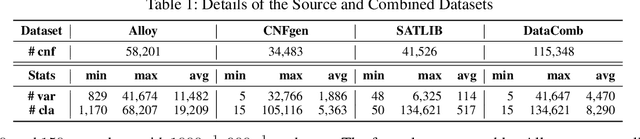
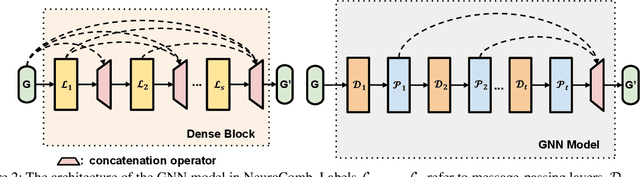
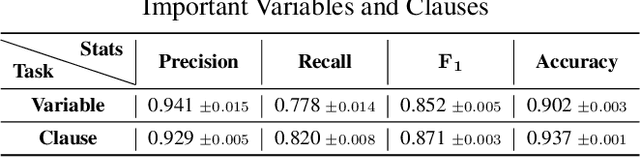
Propositional satisfiability (SAT) is an NP-complete problem that impacts many research fields, such as planning, verification, and security. Despite the remarkable success of modern SAT solvers, scalability still remains a challenge. Main stream modern SAT solvers are based on the Conflict-Driven Clause Learning (CDCL) algorithm. Recent work aimed to enhance CDCL SAT solvers by improving its variable branching heuristics through predictions generated by Graph Neural Networks (GNNs). However, so far this approach either has not made solving more effective, or has required frequent online accesses to substantial GPU resources. Aiming to make GNN improvements practical, this paper proposes an approach called NeuroComb, which builds on two insights: (1) predictions of important variables and clauses can be combined with dynamic branching into a more effective hybrid branching strategy, and (2) it is sufficient to query the neural model only once for the predictions before the SAT solving starts. Implemented as an enhancement to the classic MiniSat solver, NeuroComb allowed it to solve 18.5% more problems on the recent SATCOMP-2020 competition problem set. NeuroComb is therefore a practical approach to improving SAT solving through modern machine learning.

A Survey of Hybrid Human-Artificial Intelligence for Social Computing

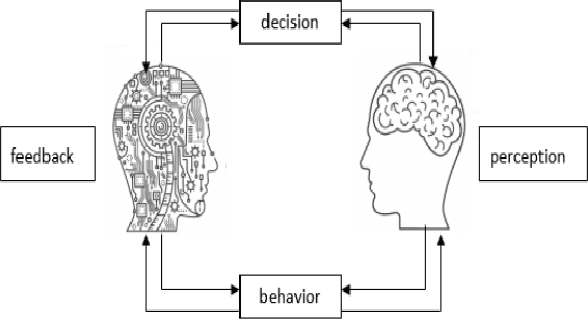
Along with the development of modern computing technology and social sciences, both theoretical research and practical applications of social computing have been continuously extended. In particular with the boom of artificial intelligence (AI), social computing is significantly influenced by AI. However, the conventional technologies of AI have drawbacks in dealing with more complicated and dynamic problems. Such deficiency can be rectified by hybrid human-artificial intelligence (H-AI) which integrates both human intelligence and AI into one unity, forming a new enhanced intelligence. H-AI in dealing with social problems shows the advantages that AI can not surpass. This paper firstly introduces the concept of H-AI. AI is the intelligence in the transition stage of H-AI, so the latest research progresses of AI in social computing are reviewed. Secondly, it summarizes typical challenges faced by AI in social computing, and makes it possible to introduce H-AI to solve these challenges. Finally, the paper proposes a holistic framework of social computing combining with H-AI, which consists of four layers: object layer, base layer, analysis layer, and application layer. It represents H-AI has significant advantages over AI in solving social problems.

A Study of the Learnability of Relational Properties

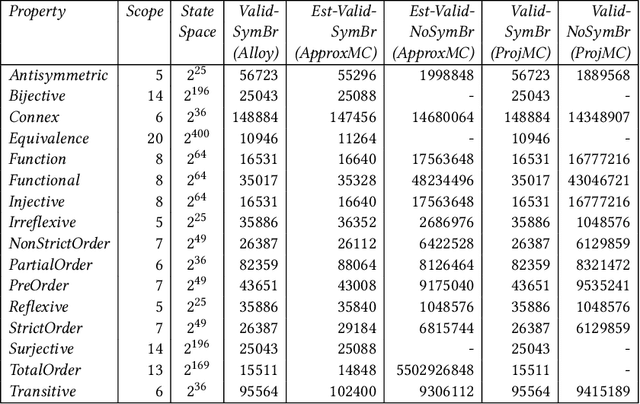
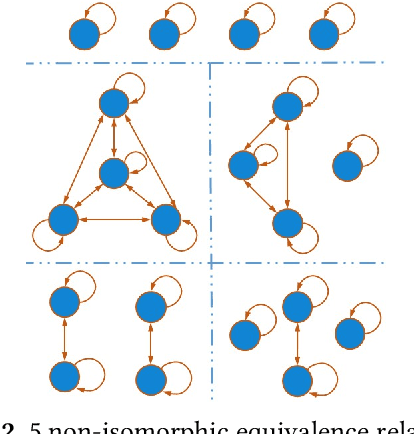
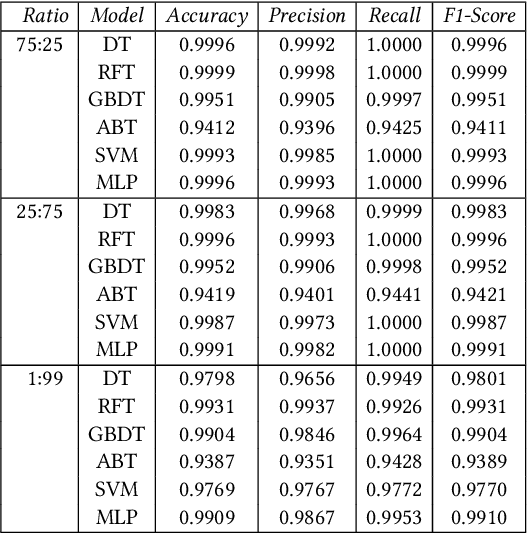
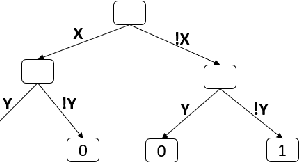
Relational properties, e.g., the connectivity structure of nodes in a distributed system, have many applications in software design and analysis. However, such properties often have to be written manually, which can be costly and error-prone. This paper introduces the MCML approach for empirically studying the learnability of a key class of such properties that can be expressed in the well-known software design language Alloy. A key novelty of MCML is quantification of the performance of and semantic differences among trained machine learning (ML) models, specifically decision trees, with respect to entire input spaces (up to a bound on the input size), and not just for given training and test datasets (as is the common practice). MCML reduces the quantification problems to the classic complexity theory problem of model counting, and employs state-of-the-art approximate and exact model counters for high efficiency. The results show that relatively simple ML models can achieve surprisingly high performance (accuracy and F1 score) at learning relational properties when evaluated in the common setting of using training and test datasets -- even when the training dataset is much smaller than the test dataset -- indicating the seeming simplicity of learning these properties. However, the use of MCML metrics based on model counting shows that the performance can degrade substantially when tested against the whole (bounded) input space, indicating the high complexity of precisely learning these properties, and the usefulness of model counting in quantifying the true accuracy.