What Makes Effective Supervision in Latent Chain-of-Thought: An Information-Theoretic Analysis

Latent Chain-of-Thought (CoT) internalizes reasoning within continuous hidden states, offering a promising alternative to verbose discrete reasoning traces. However, robust latent reasoning remains difficult because outcome supervision provides weak learning signals and leaves latent trajectories prone to semantic drift. In this work, we analyze Latent CoT from an information-theoretic perspective and identify this failure as a dual collapse: gradient attenuation along the optimization path and representational drift in the latent space. We further decompose process supervision into two complementary dimensions: Trajectory Supervision, which injects dense stepwise reasoning signals, and Space Supervision, which preserves the semantic structure of the latent manifold. Our analysis shows that rigid geometric compression can collapse the reasoning space, whereas generative reconstruction provides a more flexible semantic anchor that better preserves information capacity. To measure these effects, we introduce the Unified Latent Probe (ULP), which quantifies the mutual information between latent trajectories and explicit reasoning steps. Experiments reveal a clear Information-Performance Binding: reasoning accuracy depends on the information fidelity preserved in the latent chain. These findings provide a principled framework for latent reasoning supervision and suggest shifting from geometric imitation toward mutual information maximization. Our code is available at \href{https://github.com/EIT-NLP/Supervision-in-Latent-CoT}{this repository}.

Self-Evolving Scientific Agent Discovers Generalizable Physically-Reasoned Fluid Control

While data-intensive deep reinforcement learning can optimize complex control policies, scientific discovery in physical systems fundamentally requires an interpretable chain of reasoning that connects physical evidence to structured control architectures. Here, we present a self-evolving scientific-agent workflow, driven by large language models and iterative code generation, that automates controller construction while preserving strict interpretability and rigorous physical reasoning. Instead of adjusting weights, the agent deploys candidate strategies into physical simulations, actively diagnoses dynamic behaviors from multimodal evidence, and translates these observations into progressive source-code refinements. We demonstrate this framework on a highly non-linear fluid-structure interaction problem: an underactuated, two-joint dogfish swimmer tasked with spatial target reaching using only joint angular accelerations. Starting from a propulsive seed policy that exhibits a one-sided steering bias, the agent autonomously discovers and refines a unified controller that robustly captures all canonical targets. Remarkably, without any retraining or target-specific branching, the synthesized control policy generalizes to unseen static targets and dynamically curved pursuit trajectories. The auditable evolve log reveals an emergent control architecture built upon traveling-wave propulsion, body-frame target guidance, yaw-rate feedback, signed mean-tail curvature, and adaptive cadence relief. Our results show that an autonomous scientific agent can successfully transform accumulated physical evidence into robust, mathematically readable control policy, while maintaining a fully traceable process of scientific discovery.

Unveiling the Key Factors for Distilling Chain-of-Thought Reasoning

Large Language Models (LLMs) excel in reasoning tasks through Chain-of-Thought (CoT) prompting. However, CoT prompting greatly increases computational demands, which has prompted growing interest in distilling CoT capabilities into Small Language Models (SLMs). This study systematically examines the factors influencing CoT distillation, including the choice of granularity, format and teacher model. Through experiments involving four teacher models and seven student models across seven mathematical and commonsense reasoning datasets, we uncover three key findings: (1) Unlike LLMs, SLMs exhibit a non-monotonic relationship with granularity, with stronger models benefiting from finer-grained reasoning and weaker models performing better with simpler CoT supervision; (2) CoT format significantly impacts LLMs but has minimal effect on SLMs, likely due to their reliance on supervised fine-tuning rather than pretraining preferences; (3) Stronger teacher models do NOT always produce better student models, as diversity and complexity in CoT supervision can outweigh accuracy alone. These findings emphasize the need to tailor CoT strategies to specific student model, offering actionable insights for optimizing CoT distillation in SLMs. The code and datasets are available at https://github.com/EIT-NLP/Distilling-CoT-Reasoning.

Towards Accurate and Efficient Sub-8-Bit Integer Training

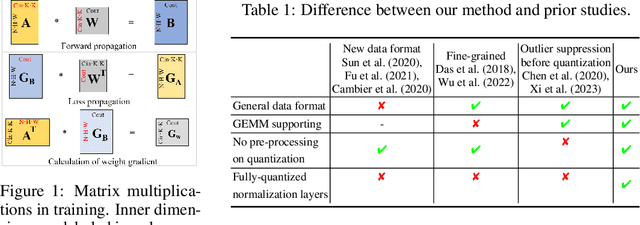
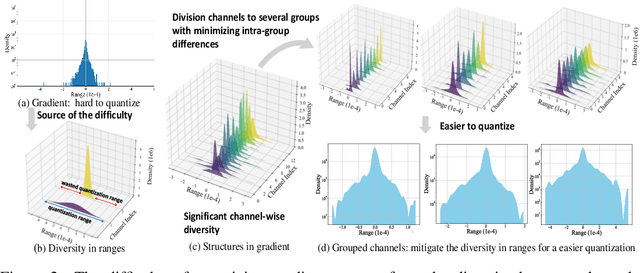
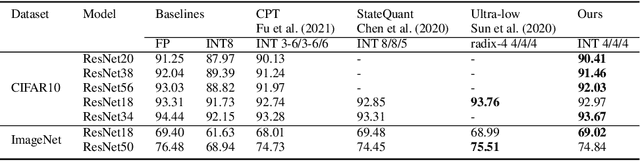
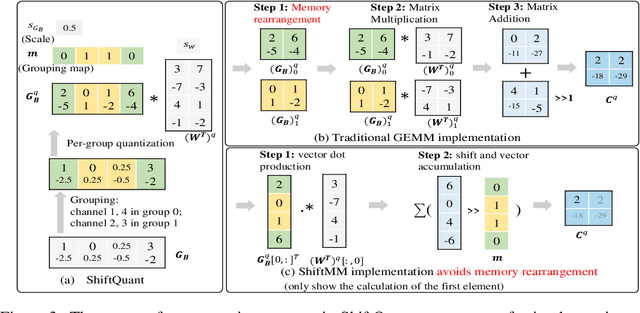
Neural network training is a memory- and compute-intensive task. Quantization, which enables low-bitwidth formats in training, can significantly mitigate the workload. To reduce quantization error, recent methods have developed new data formats and additional pre-processing operations on quantizers. However, it remains quite challenging to achieve high accuracy and efficiency simultaneously. In this paper, we explore sub-8-bit integer training from its essence of gradient descent optimization. Our integer training framework includes two components: ShiftQuant to realize accurate gradient estimation, and L1 normalization to smoothen the loss landscape. ShiftQuant attains performance that approaches the theoretical upper bound of group quantization. Furthermore, it liberates group quantization from inefficient memory rearrangement. The L1 normalization facilitates the implementation of fully quantized normalization layers with impressive convergence accuracy. Our method frees sub-8-bit integer training from pre-processing and supports general devices. This framework achieves negligible accuracy loss across various neural networks and tasks ($0.92\%$ on 4-bit ResNets, $0.61\%$ on 6-bit Transformers). The prototypical implementation of ShiftQuant achieves more than $1.85\times/15.3\%$ performance improvement on CPU/GPU compared to its FP16 counterparts, and $33.9\%$ resource consumption reduction on FPGA than the FP16 counterparts. The proposed fully-quantized L1 normalization layers achieve more than $35.54\%$ improvement in throughout on CPU compared to traditional L2 normalization layers. Moreover, theoretical analysis verifies the advancement of our method.