Off-OAB: Off-Policy Policy Gradient Method with Optimal Action-Dependent Baseline

Policy-based methods have achieved remarkable success in solving challenging reinforcement learning problems. Among these methods, off-policy policy gradient methods are particularly important due to that they can benefit from off-policy data. However, these methods suffer from the high variance of the off-policy policy gradient (OPPG) estimator, which results in poor sample efficiency during training. In this paper, we propose an off-policy policy gradient method with the optimal action-dependent baseline (Off-OAB) to mitigate this variance issue. Specifically, this baseline maintains the OPPG estimator's unbiasedness while theoretically minimizing its variance. To enhance practical computational efficiency, we design an approximated version of this optimal baseline. Utilizing this approximation, our method (Off-OAB) aims to decrease the OPPG estimator's variance during policy optimization. We evaluate the proposed Off-OAB method on six representative tasks from OpenAI Gym and MuJoCo, where it demonstrably surpasses state-of-the-art methods on the majority of these tasks.

Qualitative Measurements of Policy Discrepancy for Return-based Deep Q-Network

The deep Q-network (DQN) and return-based reinforcement learning are two promising algorithms proposed in recent years. DQN brings advances to complex sequential decision problems, while return-based algorithms have advantages in making use of sample trajectories. In this paper, we propose a general framework to combine DQN and most of the return-based reinforcement learning algorithms, named R-DQN. We show the performance of traditional DQN can be improved effectively by introducing return-based reinforcement learning. In order to further improve the R-DQN, we design a strategy with two measurements which can qualitatively measure the policy discrepancy. Moreover, we give the two measurements' bounds in the proposed R-DQN framework. We show that algorithms with our strategy can accurately express the trace coefficient and achieve a better approximation to return. The experiments, conducted on several representative tasks from the OpenAI Gym library, validate the effectiveness of the proposed measurements. The results also show that the algorithms with our strategy outperform the state-of-the-art methods.

A Unified Approach for Multi-step Temporal-Difference Learning with Eligibility Traces in Reinforcement Learning

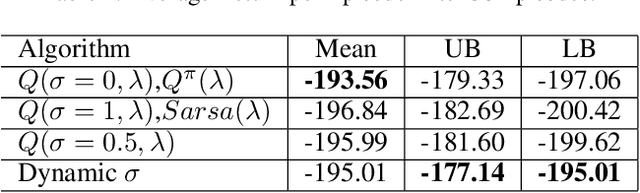
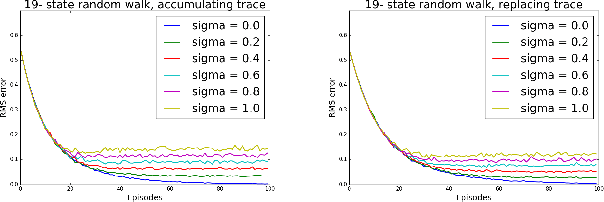
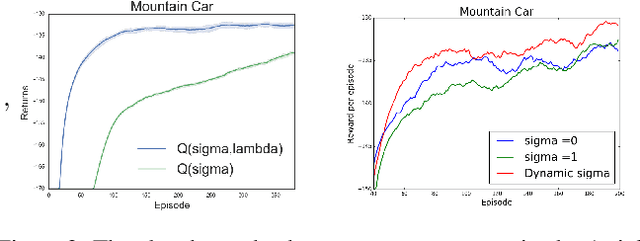
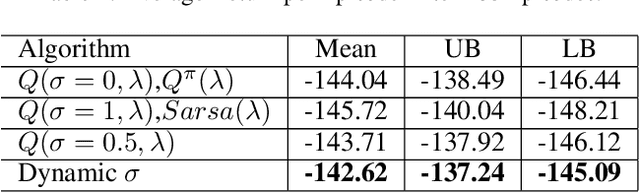
Recently, a new multi-step temporal learning algorithm, called $Q(\sigma)$, unifies $n$-step Tree-Backup (when $\sigma=0$) and $n$-step Sarsa (when $\sigma=1$) by introducing a sampling parameter $\sigma$. However, similar to other multi-step temporal-difference learning algorithms, $Q(\sigma)$ needs much memory consumption and computation time. Eligibility trace is an important mechanism to transform the off-line updates into efficient on-line ones which consume less memory and computation time. In this paper, we further develop the original $Q(\sigma)$, combine it with eligibility traces and propose a new algorithm, called $Q(\sigma ,\lambda)$, in which $\lambda$ is trace-decay parameter. This idea unifies Sarsa$(\lambda)$ (when $\sigma =1$) and $Q^{\pi}(\lambda)$ (when $\sigma =0$). Furthermore, we give an upper error bound of $Q(\sigma ,\lambda)$ policy evaluation algorithm. We prove that $Q(\sigma,\lambda)$ control algorithm can converge to the optimal value function exponentially. We also empirically compare it with conventional temporal-difference learning methods. Results show that, with an intermediate value of $\sigma$, $Q(\sigma ,\lambda)$ creates a mixture of the existing algorithms that can learn the optimal value significantly faster than the extreme end ($\sigma=0$, or $1$).

Two-Bit Networks for Deep Learning on Resource-Constrained Embedded Devices

With the rapid proliferation of Internet of Things and intelligent edge devices, there is an increasing need for implementing machine learning algorithms, including deep learning, on resource-constrained mobile embedded devices with limited memory and computation power. Typical large Convolutional Neural Networks (CNNs) need large amounts of memory and computational power, and cannot be deployed on embedded devices efficiently. We present Two-Bit Networks (TBNs) for model compression of CNNs with edge weights constrained to (-2, -1, 1, 2), which can be encoded with two bits. Our approach can reduce the memory usage and improve computational efficiency significantly while achieving good performance in terms of classification accuracy, thus representing a reasonable tradeoff between model size and performance.