SPAIC: A Spike-based Artificial Intelligence Computing Framework

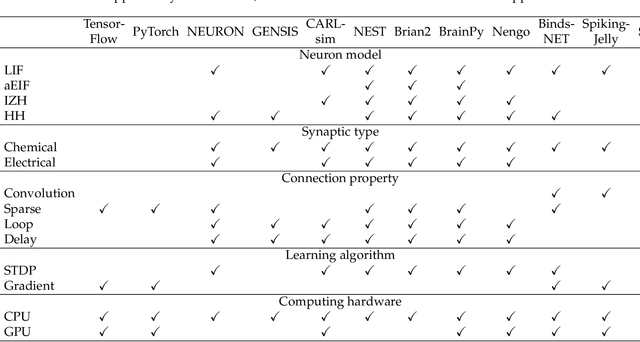
Neuromorphic computing is an emerging research field that aims to develop new intelligent systems by integrating theories and technologies from multi-disciplines such as neuroscience and deep learning. Currently, there have been various software frameworks developed for the related fields, but there is a lack of an efficient framework dedicated for spike-based computing models and algorithms. In this work, we present a Python based spiking neural network (SNN) simulation and training framework, aka SPAIC that aims to support brain-inspired model and algorithm researches integrated with features from both deep learning and neuroscience. To integrate different methodologies from the two overwhelming disciplines, and balance between flexibility and efficiency, SPAIC is designed with neuroscience-style frontend and deep learning backend structure. We provide a wide range of examples including neural circuits Simulation, deep SNN learning and neuromorphic applications, demonstrating the concise coding style and wide usability of our framework. The SPAIC is a dedicated spike-based artificial intelligence computing platform, which will significantly facilitate the design, prototype and validation of new models, theories and applications. Being user-friendly, flexible and high-performance, it will help accelerate the rapid growth and wide applicability of neuromorphic computing research.

Spectral-graph Based Classifications: Linear Regression for Classification and Normalized Radial Basis Function Network

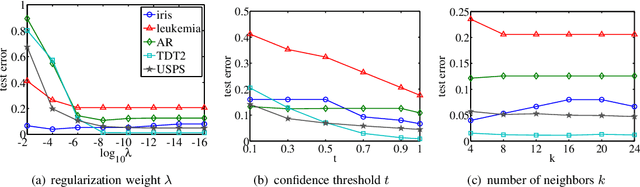
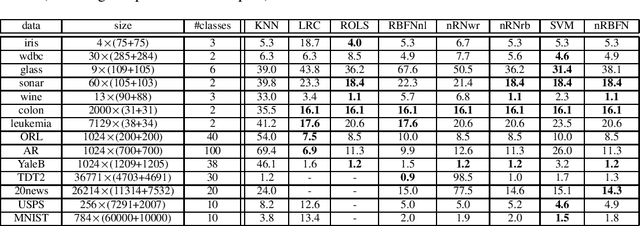
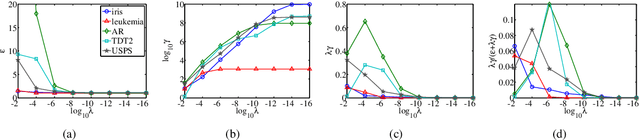
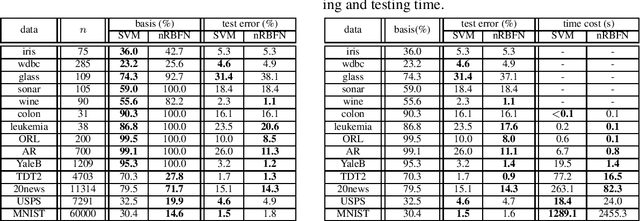
Spectral graph theory has been widely applied in unsupervised and semi-supervised learning. In this paper, we find for the first time, to our knowledge, that it also plays a concrete role in supervised classification. It turns out that two classifiers are inherently related to the theory: linear regression for classification (LRC) and normalized radial basis function network (nRBFN), corresponding to linear and nonlinear kernel respectively. The spectral graph theory provides us with a new insight into a fundamental aspect of classification: the tradeoff between fitting error and overfitting risk. With the theory, ideal working conditions for LRC and nRBFN are presented, which ensure not only zero fitting error but also low overfitting risk. For quantitative analysis, two concepts, the fitting error and the spectral risk (indicating overfitting), have been defined. Their bounds for nRBFN and LRC are derived. A special result shows that the spectral risk of nRBFN is lower bounded by the number of classes and upper bounded by the size of radial basis. When the conditions are not met exactly, the classifiers will pursue the minimum fitting error, running into the risk of overfitting. It turns out that $\ell_2$-norm regularization can be applied to control overfitting. Its effect is explored under the spectral context. It is found that the two terms in the $\ell_2$-regularized objective are one-one correspondent to the fitting error and the spectral risk, revealing a tradeoff between the two quantities. Concerning practical performance, we devise a basis selection strategy to address the main problem hindering the applications of (n)RBFN. With the strategy, nRBFN is easy to implement yet flexible. Experiments on 14 benchmark data sets show the performance of nRBFN is comparable to that of SVM, whereas the parameter tuning of nRBFN is much easier, leading to reduction of model selection time.

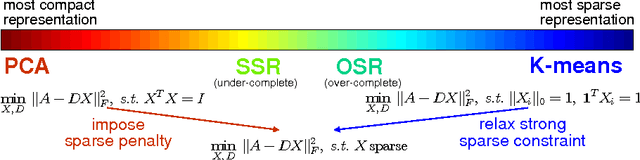
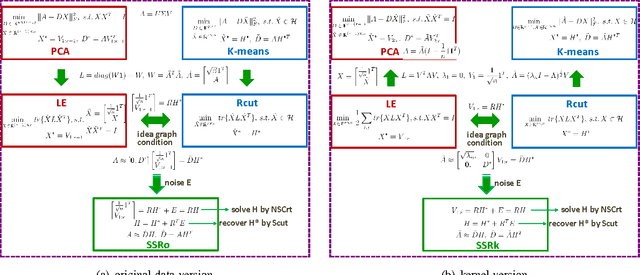
Spectral Sparse Representation for Clustering: Evolved from PCA, K-means, Laplacian Eigenmap, and Ratio Cut

Dimensionality reduction, cluster analysis, and sparse representation are basic components in machine learning. However, their relationships have not yet been fully investigated. In this paper, we find that the spectral graph theory underlies a series of these elementary methods and can unify them into a complete framework. The methods include PCA, K-means, Laplacian eigenmap (LE), ratio cut (Rcut), and a new sparse representation method developed by us, called spectral sparse representation (SSR). Further, extended relations to conventional over-complete sparse representations (e.g., method of optimal directions, KSVD), manifold learning (e.g., kernel PCA, multidimensional scaling, Isomap, locally linear embedding), and subspace clustering (e.g., sparse subspace clustering, low-rank representation) are incorporated. We show that, under an ideal condition from the spectral graph theory, PCA, K-means, LE, and Rcut are unified together. And when the condition is relaxed, the unification evolves to SSR, which lies in the intermediate between PCA/LE and K-mean/Rcut. An efficient algorithm, NSCrt, is developed to solve the sparse codes of SSR. SSR combines merits of both sides: its sparse codes reduce dimensionality of data meanwhile revealing cluster structure. For its inherent relation to cluster analysis, the codes of SSR can be directly used for clustering. Scut, a clustering approach derived from SSR reaches the state-of-the-art performance in the spectral clustering family. The one-shot solution obtained by Scut is comparable to the optimal result of K-means that are run many times. Experiments on various data sets demonstrate the properties and strengths of SSR, NSCrt, and Scut.

Two-Bit Networks for Deep Learning on Resource-Constrained Embedded Devices

With the rapid proliferation of Internet of Things and intelligent edge devices, there is an increasing need for implementing machine learning algorithms, including deep learning, on resource-constrained mobile embedded devices with limited memory and computation power. Typical large Convolutional Neural Networks (CNNs) need large amounts of memory and computational power, and cannot be deployed on embedded devices efficiently. We present Two-Bit Networks (TBNs) for model compression of CNNs with edge weights constrained to (-2, -1, 1, 2), which can be encoded with two bits. Our approach can reduce the memory usage and improve computational efficiency significantly while achieving good performance in terms of classification accuracy, thus representing a reasonable tradeoff between model size and performance.

Sparse Principal Component Analysis via Rotation and Truncation

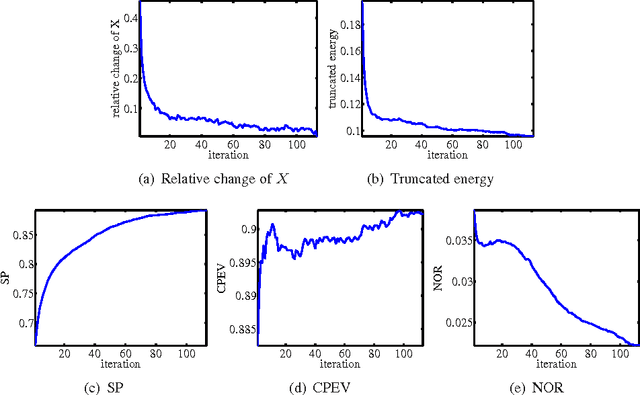
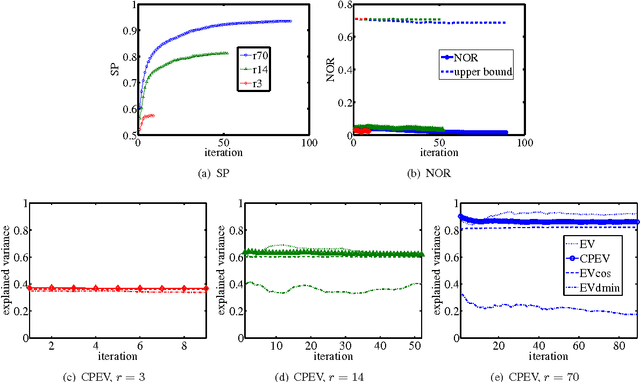
Sparse principal component analysis (sparse PCA) aims at finding a sparse basis to improve the interpretability over the dense basis of PCA, meanwhile the sparse basis should cover the data subspace as much as possible. In contrast to most of existing work which deal with the problem by adding some sparsity penalties on various objectives of PCA, in this paper, we propose a new method SPCArt, whose motivation is to find a rotation matrix and a sparse basis such that the sparse basis approximates the basis of PCA after the rotation. The algorithm of SPCArt consists of three alternating steps: rotate PCA basis, truncate small entries, and update the rotation matrix. Its performance bounds are also given. SPCArt is efficient, with each iteration scaling linearly with the data dimension. It is easy to choose parameters in SPCArt, due to its explicit physical explanations. Besides, we give a unified view to several existing sparse PCA methods and discuss the connection with SPCArt. Some ideas in SPCArt are extended to GPower, a popular sparse PCA algorithm, to overcome its drawback. Experimental results demonstrate that SPCArt achieves the state-of-the-art performance. It also achieves a good tradeoff among various criteria, including sparsity, explained variance, orthogonality, balance of sparsity among loadings, and computational speed.