Spectral-graph Based Classifications: Linear Regression for Classification and Normalized Radial Basis Function Network

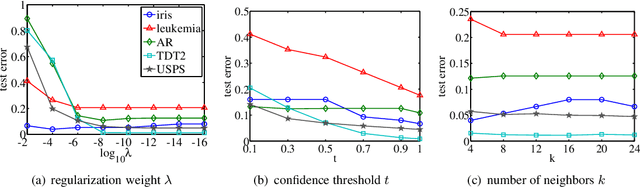
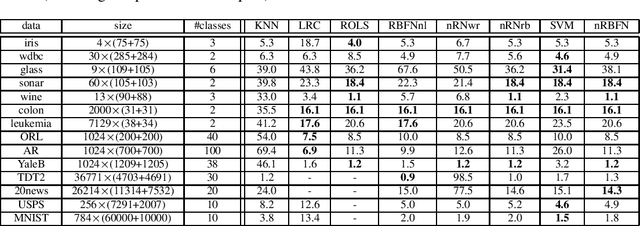
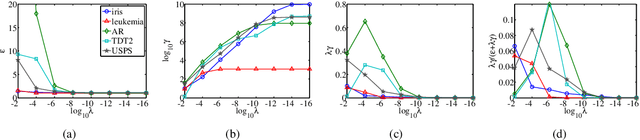
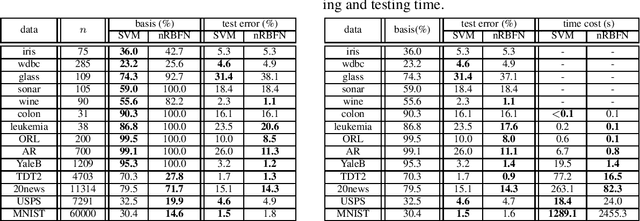
Spectral graph theory has been widely applied in unsupervised and semi-supervised learning. In this paper, we find for the first time, to our knowledge, that it also plays a concrete role in supervised classification. It turns out that two classifiers are inherently related to the theory: linear regression for classification (LRC) and normalized radial basis function network (nRBFN), corresponding to linear and nonlinear kernel respectively. The spectral graph theory provides us with a new insight into a fundamental aspect of classification: the tradeoff between fitting error and overfitting risk. With the theory, ideal working conditions for LRC and nRBFN are presented, which ensure not only zero fitting error but also low overfitting risk. For quantitative analysis, two concepts, the fitting error and the spectral risk (indicating overfitting), have been defined. Their bounds for nRBFN and LRC are derived. A special result shows that the spectral risk of nRBFN is lower bounded by the number of classes and upper bounded by the size of radial basis. When the conditions are not met exactly, the classifiers will pursue the minimum fitting error, running into the risk of overfitting. It turns out that $\ell_2$-norm regularization can be applied to control overfitting. Its effect is explored under the spectral context. It is found that the two terms in the $\ell_2$-regularized objective are one-one correspondent to the fitting error and the spectral risk, revealing a tradeoff between the two quantities. Concerning practical performance, we devise a basis selection strategy to address the main problem hindering the applications of (n)RBFN. With the strategy, nRBFN is easy to implement yet flexible. Experiments on 14 benchmark data sets show the performance of nRBFN is comparable to that of SVM, whereas the parameter tuning of nRBFN is much easier, leading to reduction of model selection time.

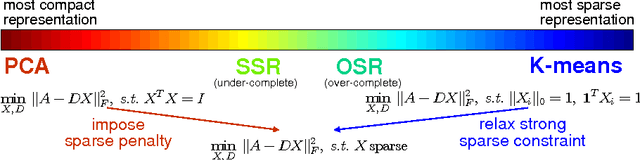
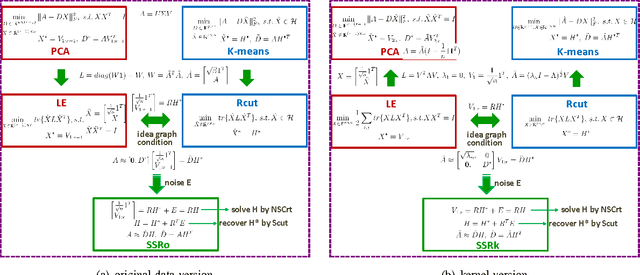
Spectral Sparse Representation for Clustering: Evolved from PCA, K-means, Laplacian Eigenmap, and Ratio Cut

Dimensionality reduction, cluster analysis, and sparse representation are basic components in machine learning. However, their relationships have not yet been fully investigated. In this paper, we find that the spectral graph theory underlies a series of these elementary methods and can unify them into a complete framework. The methods include PCA, K-means, Laplacian eigenmap (LE), ratio cut (Rcut), and a new sparse representation method developed by us, called spectral sparse representation (SSR). Further, extended relations to conventional over-complete sparse representations (e.g., method of optimal directions, KSVD), manifold learning (e.g., kernel PCA, multidimensional scaling, Isomap, locally linear embedding), and subspace clustering (e.g., sparse subspace clustering, low-rank representation) are incorporated. We show that, under an ideal condition from the spectral graph theory, PCA, K-means, LE, and Rcut are unified together. And when the condition is relaxed, the unification evolves to SSR, which lies in the intermediate between PCA/LE and K-mean/Rcut. An efficient algorithm, NSCrt, is developed to solve the sparse codes of SSR. SSR combines merits of both sides: its sparse codes reduce dimensionality of data meanwhile revealing cluster structure. For its inherent relation to cluster analysis, the codes of SSR can be directly used for clustering. Scut, a clustering approach derived from SSR reaches the state-of-the-art performance in the spectral clustering family. The one-shot solution obtained by Scut is comparable to the optimal result of K-means that are run many times. Experiments on various data sets demonstrate the properties and strengths of SSR, NSCrt, and Scut.

Sparse Principal Component Analysis via Rotation and Truncation

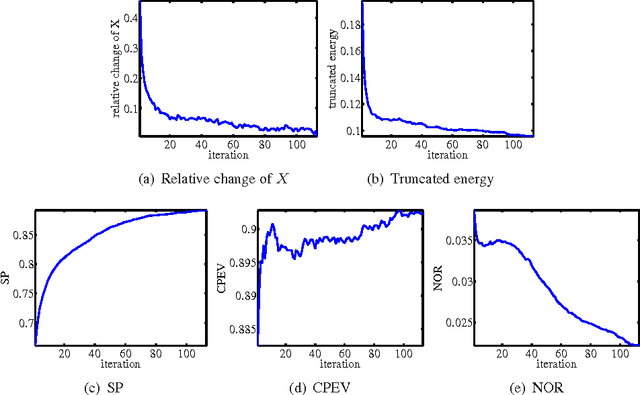
Sparse principal component analysis (sparse PCA) aims at finding a sparse basis to improve the interpretability over the dense basis of PCA, meanwhile the sparse basis should cover the data subspace as much as possible. In contrast to most of existing work which deal with the problem by adding some sparsity penalties on various objectives of PCA, in this paper, we propose a new method SPCArt, whose motivation is to find a rotation matrix and a sparse basis such that the sparse basis approximates the basis of PCA after the rotation. The algorithm of SPCArt consists of three alternating steps: rotate PCA basis, truncate small entries, and update the rotation matrix. Its performance bounds are also given. SPCArt is efficient, with each iteration scaling linearly with the data dimension. It is easy to choose parameters in SPCArt, due to its explicit physical explanations. Besides, we give a unified view to several existing sparse PCA methods and discuss the connection with SPCArt. Some ideas in SPCArt are extended to GPower, a popular sparse PCA algorithm, to overcome its drawback. Experimental results demonstrate that SPCArt achieves the state-of-the-art performance. It also achieves a good tradeoff among various criteria, including sparsity, explained variance, orthogonality, balance of sparsity among loadings, and computational speed.