Spectral Sparse Representation for Clustering: Evolved from PCA, K-means, Laplacian Eigenmap, and Ratio Cut
Paper and Code
May 19, 2017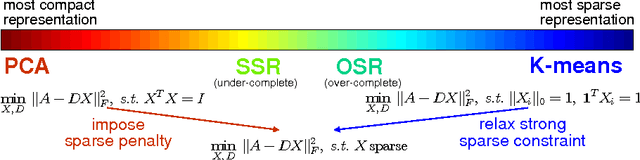

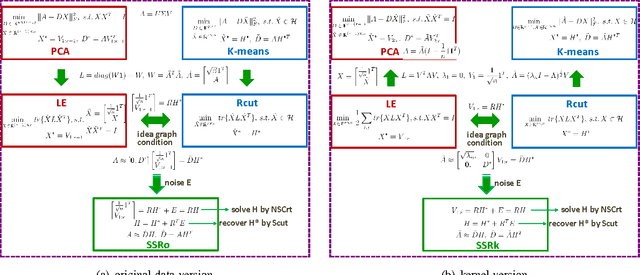
Dimensionality reduction, cluster analysis, and sparse representation are basic components in machine learning. However, their relationships have not yet been fully investigated. In this paper, we find that the spectral graph theory underlies a series of these elementary methods and can unify them into a complete framework. The methods include PCA, K-means, Laplacian eigenmap (LE), ratio cut (Rcut), and a new sparse representation method developed by us, called spectral sparse representation (SSR). Further, extended relations to conventional over-complete sparse representations (e.g., method of optimal directions, KSVD), manifold learning (e.g., kernel PCA, multidimensional scaling, Isomap, locally linear embedding), and subspace clustering (e.g., sparse subspace clustering, low-rank representation) are incorporated. We show that, under an ideal condition from the spectral graph theory, PCA, K-means, LE, and Rcut are unified together. And when the condition is relaxed, the unification evolves to SSR, which lies in the intermediate between PCA/LE and K-mean/Rcut. An efficient algorithm, NSCrt, is developed to solve the sparse codes of SSR. SSR combines merits of both sides: its sparse codes reduce dimensionality of data meanwhile revealing cluster structure. For its inherent relation to cluster analysis, the codes of SSR can be directly used for clustering. Scut, a clustering approach derived from SSR reaches the state-of-the-art performance in the spectral clustering family. The one-shot solution obtained by Scut is comparable to the optimal result of K-means that are run many times. Experiments on various data sets demonstrate the properties and strengths of SSR, NSCrt, and Scut.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge