Sparse Principal Component Analysis via Rotation and Truncation

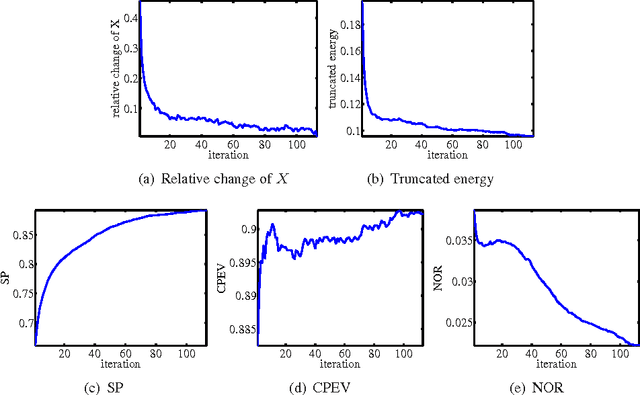
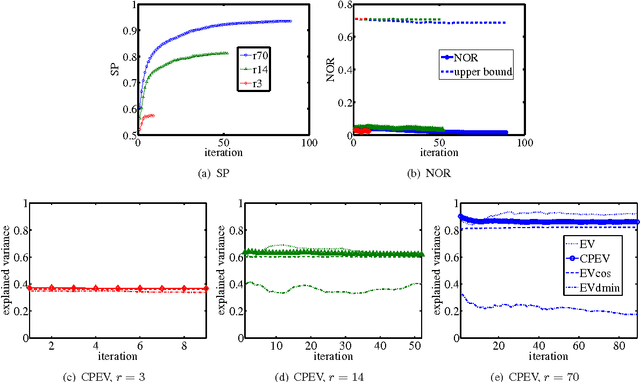
Sparse principal component analysis (sparse PCA) aims at finding a sparse basis to improve the interpretability over the dense basis of PCA, meanwhile the sparse basis should cover the data subspace as much as possible. In contrast to most of existing work which deal with the problem by adding some sparsity penalties on various objectives of PCA, in this paper, we propose a new method SPCArt, whose motivation is to find a rotation matrix and a sparse basis such that the sparse basis approximates the basis of PCA after the rotation. The algorithm of SPCArt consists of three alternating steps: rotate PCA basis, truncate small entries, and update the rotation matrix. Its performance bounds are also given. SPCArt is efficient, with each iteration scaling linearly with the data dimension. It is easy to choose parameters in SPCArt, due to its explicit physical explanations. Besides, we give a unified view to several existing sparse PCA methods and discuss the connection with SPCArt. Some ideas in SPCArt are extended to GPower, a popular sparse PCA algorithm, to overcome its drawback. Experimental results demonstrate that SPCArt achieves the state-of-the-art performance. It also achieves a good tradeoff among various criteria, including sparsity, explained variance, orthogonality, balance of sparsity among loadings, and computational speed.