Spectral-graph Based Classifications: Linear Regression for Classification and Normalized Radial Basis Function Network
Paper and Code
Jun 13, 2017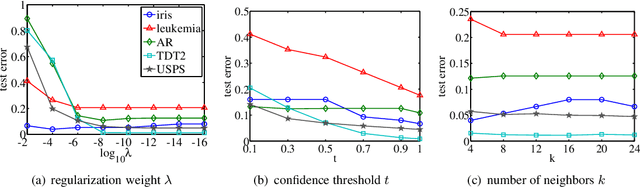
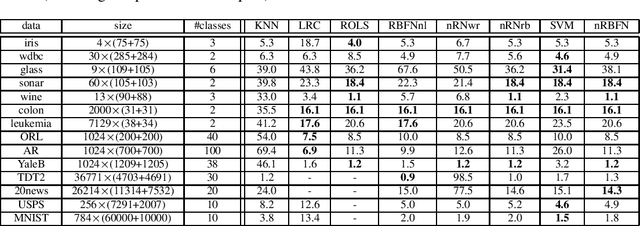
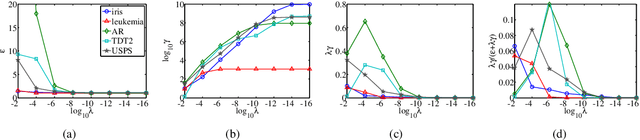
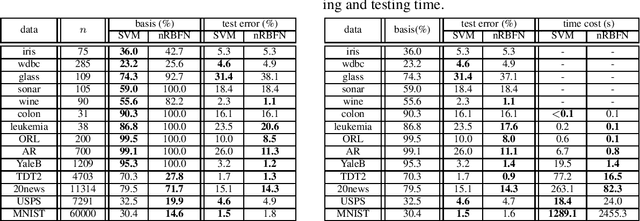
Spectral graph theory has been widely applied in unsupervised and semi-supervised learning. In this paper, we find for the first time, to our knowledge, that it also plays a concrete role in supervised classification. It turns out that two classifiers are inherently related to the theory: linear regression for classification (LRC) and normalized radial basis function network (nRBFN), corresponding to linear and nonlinear kernel respectively. The spectral graph theory provides us with a new insight into a fundamental aspect of classification: the tradeoff between fitting error and overfitting risk. With the theory, ideal working conditions for LRC and nRBFN are presented, which ensure not only zero fitting error but also low overfitting risk. For quantitative analysis, two concepts, the fitting error and the spectral risk (indicating overfitting), have been defined. Their bounds for nRBFN and LRC are derived. A special result shows that the spectral risk of nRBFN is lower bounded by the number of classes and upper bounded by the size of radial basis. When the conditions are not met exactly, the classifiers will pursue the minimum fitting error, running into the risk of overfitting. It turns out that $\ell_2$-norm regularization can be applied to control overfitting. Its effect is explored under the spectral context. It is found that the two terms in the $\ell_2$-regularized objective are one-one correspondent to the fitting error and the spectral risk, revealing a tradeoff between the two quantities. Concerning practical performance, we devise a basis selection strategy to address the main problem hindering the applications of (n)RBFN. With the strategy, nRBFN is easy to implement yet flexible. Experiments on 14 benchmark data sets show the performance of nRBFN is comparable to that of SVM, whereas the parameter tuning of nRBFN is much easier, leading to reduction of model selection time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge