A Unified Approach for Multi-step Temporal-Difference Learning with Eligibility Traces in Reinforcement Learning
Paper and Code
Feb 09, 2018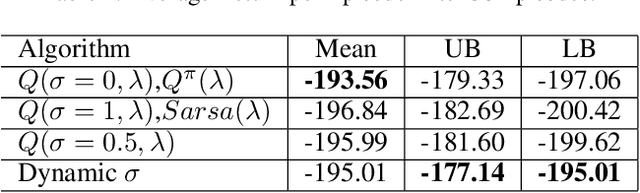
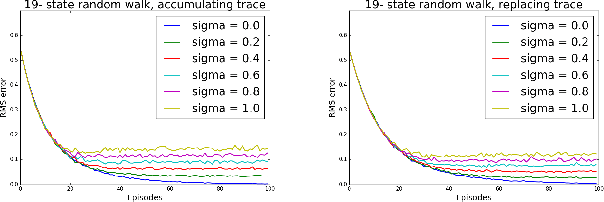
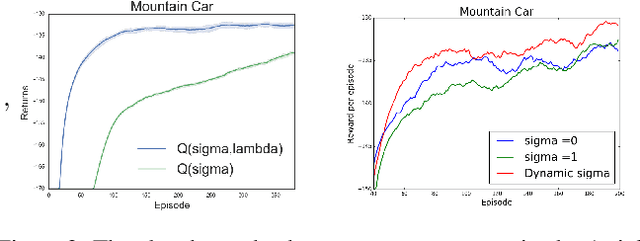
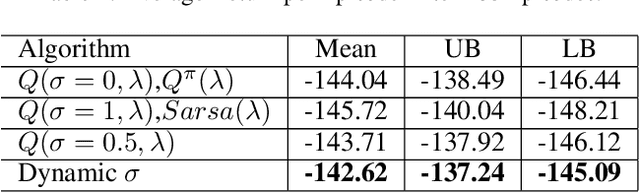
Recently, a new multi-step temporal learning algorithm, called $Q(\sigma)$, unifies $n$-step Tree-Backup (when $\sigma=0$) and $n$-step Sarsa (when $\sigma=1$) by introducing a sampling parameter $\sigma$. However, similar to other multi-step temporal-difference learning algorithms, $Q(\sigma)$ needs much memory consumption and computation time. Eligibility trace is an important mechanism to transform the off-line updates into efficient on-line ones which consume less memory and computation time. In this paper, we further develop the original $Q(\sigma)$, combine it with eligibility traces and propose a new algorithm, called $Q(\sigma ,\lambda)$, in which $\lambda$ is trace-decay parameter. This idea unifies Sarsa$(\lambda)$ (when $\sigma =1$) and $Q^{\pi}(\lambda)$ (when $\sigma =0$). Furthermore, we give an upper error bound of $Q(\sigma ,\lambda)$ policy evaluation algorithm. We prove that $Q(\sigma,\lambda)$ control algorithm can converge to the optimal value function exponentially. We also empirically compare it with conventional temporal-difference learning methods. Results show that, with an intermediate value of $\sigma$, $Q(\sigma ,\lambda)$ creates a mixture of the existing algorithms that can learn the optimal value significantly faster than the extreme end ($\sigma=0$, or $1$).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge