GalleryGPT: Analyzing Paintings with Large Multimodal Models

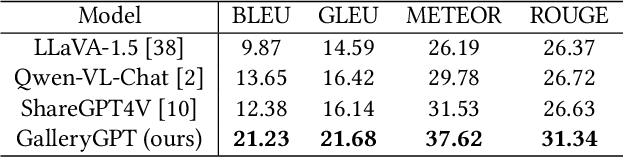
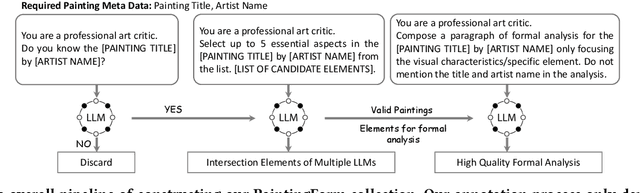
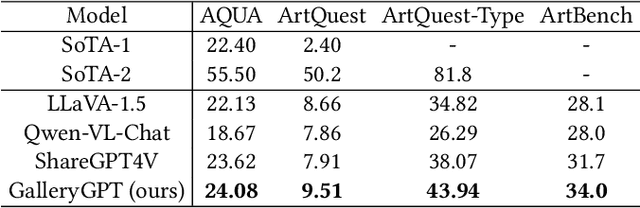
Artwork analysis is important and fundamental skill for art appreciation, which could enrich personal aesthetic sensibility and facilitate the critical thinking ability. Understanding artworks is challenging due to its subjective nature, diverse interpretations, and complex visual elements, requiring expertise in art history, cultural background, and aesthetic theory. However, limited by the data collection and model ability, previous works for automatically analyzing artworks mainly focus on classification, retrieval, and other simple tasks, which is far from the goal of AI. To facilitate the research progress, in this paper, we step further to compose comprehensive analysis inspired by the remarkable perception and generation ability of large multimodal models. Specifically, we first propose a task of composing paragraph analysis for artworks, i.e., painting in this paper, only focusing on visual characteristics to formulate more comprehensive understanding of artworks. To support the research on formal analysis, we collect a large dataset PaintingForm, with about 19k painting images and 50k analysis paragraphs. We further introduce a superior large multimodal model for painting analysis composing, dubbed GalleryGPT, which is slightly modified and fine-tuned based on LLaVA architecture leveraging our collected data. We conduct formal analysis generation and zero-shot experiments across several datasets to assess the capacity of our model. The results show remarkable performance improvements comparing with powerful baseline LMMs, demonstrating its superb ability of art analysis and generalization. \textcolor{blue}{The codes and model are available at: https://github.com/steven640pixel/GalleryGPT.

Math-LLaVA: Bootstrapping Mathematical Reasoning for Multimodal Large Language Models

Large language models (LLMs) have demonstrated impressive reasoning capabilities, particularly in textual mathematical problem-solving. However, existing open-source image instruction fine-tuning datasets, containing limited question-answer pairs per image, do not fully exploit visual information to enhance the multimodal mathematical reasoning capabilities of Multimodal LLMs (MLLMs). To bridge this gap, we address the lack of high-quality, diverse multimodal mathematical datasets by collecting 40K high-quality images with question-answer pairs from 24 existing datasets and synthesizing 320K new pairs, creating the MathV360K dataset, which enhances both the breadth and depth of multimodal mathematical questions. We introduce Math-LLaVA, a LLaVA-1.5-based model fine-tuned with MathV360K. This novel approach significantly improves the multimodal mathematical reasoning capabilities of LLaVA-1.5, achieving a 19-point increase and comparable performance to GPT-4V on MathVista's minitest split. Furthermore, Math-LLaVA demonstrates enhanced generalizability, showing substantial improvements on the MMMU benchmark. Our research highlights the importance of dataset diversity and synthesis in advancing MLLMs' mathematical reasoning abilities. The code and data are available at: \url{https://github.com/HZQ950419/Math-LLaVA}.

Non-Autoregressive Sentence Ordering

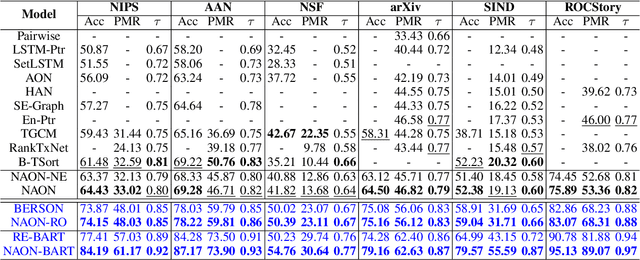
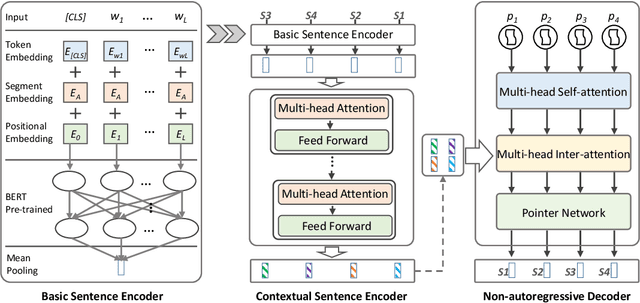
Existing sentence ordering approaches generally employ encoder-decoder frameworks with the pointer net to recover the coherence by recurrently predicting each sentence step-by-step. Such an autoregressive manner only leverages unilateral dependencies during decoding and cannot fully explore the semantic dependency between sentences for ordering. To overcome these limitations, in this paper, we propose a novel Non-Autoregressive Ordering Network, dubbed \textit{NAON}, which explores bilateral dependencies between sentences and predicts the sentence for each position in parallel. We claim that the non-autoregressive manner is not just applicable but also particularly suitable to the sentence ordering task because of two peculiar characteristics of the task: 1) each generation target is in deterministic length, and 2) the sentences and positions should match exclusively. Furthermore, to address the repetition issue of the naive non-autoregressive Transformer, we introduce an exclusive loss to constrain the exclusiveness between positions and sentences. To verify the effectiveness of the proposed model, we conduct extensive experiments on several common-used datasets and the experimental results show that our method outperforms all the autoregressive approaches and yields competitive performance compared with the state-of-the-arts. The codes are available at: \url{https://github.com/steven640pixel/nonautoregressive-sentence-ordering}.

Solving Math Word Problems with Reexamination

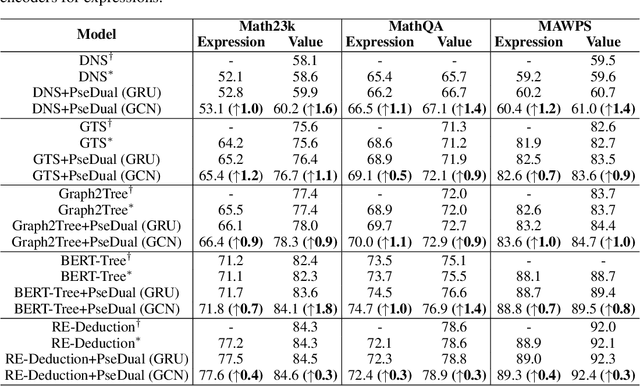
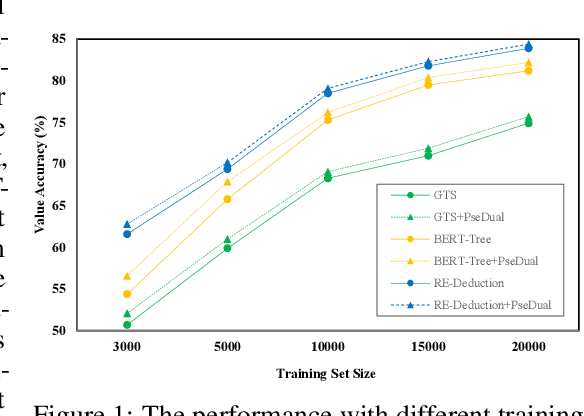
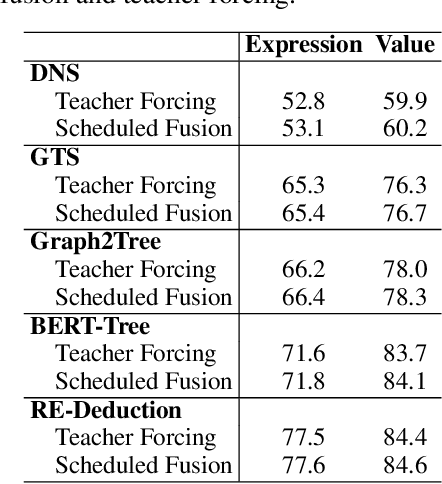
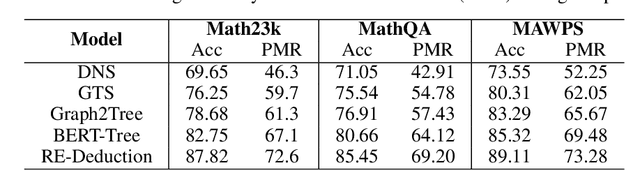
Math word problem (MWP) solving aims to understand the descriptive math problem and calculate the result, for which previous efforts are mostly devoted to upgrade different technical modules. This paper brings a different perspective of \textit{reexamination process} during training by introducing a pseudo-dual task to enhance the MWP solving. We propose a pseudo-dual (PseDual) learning scheme to model such process, which is model-agnostic thus can be adapted to any existing MWP solvers. The pseudo-dual task is specifically defined as filling the numbers in the expression back into the original word problem with numbers masked. To facilitate the effective joint learning of the two tasks, we further design a scheduled fusion strategy for the number infilling task, which smoothly switches the input from the ground-truth math expressions to the predicted ones. Our pseudo-dual learning scheme has been tested and proven effective when being equipped in several representative MWP solvers through empirical studies. \textit{The codes and trained models are available at:} \url{https://github.com/steven640pixel/PsedualMWP}. \end{abstract}

Non-Autoregressive Math Word Problem Solver with Unified Tree Structure

Existing MWP solvers employ sequence or binary tree to present the solution expression and decode it from given problem description. However, such structures fail to handle the identical variants derived via mathematical manipulation, e.g., $(a_1+a_2)*a_3$ and $a_1*a_3+a_2*a_3$ are for the same problem but formulating different expression sequences and trees, which would raise two issues in MWP solving: 1) different output solutions for the same input problem, making the model hard to learn the mapping function between input and output spaces, and 2) difficulty of evaluating solution expression that indicates wrong between the above examples. To address these issues, we first introduce a unified tree structure to present expression, where the elements are permutable and identical for all the expression variants. We then propose a novel non-autoregressive solver, dubbed MWP-NAS, to parse the problem and reason the solution expression based on the unified tree. For the second issue, to handle the variants in evaluation, we propose to match the unified tree and design a path-based metric to evaluate the partial accuracy of expression. Extensive experiments have been conducted on Math23K and MAWPS, and the results demonstrate the effectiveness of the proposed MWP-NAS. The codes and checkpoints are available at: https://github.com/mengqunhan/MWP-NAS