Fast Algorithms for Poker Require Modelling it as a Sequential Bayesian Game

Many recent results in imperfect information games were only formulated for, or evaluated on, poker and poker-like games such as liar's dice. We argue that sequential Bayesian games constitute a natural class of games for generalizing these results. In particular, this model allows for an elegant formulation of the counterfactual regret minimization algorithm, called public-state CFR (PS-CFR), which naturally lends itself to an efficient implementation. Empirically, solving a poker subgame with 10^7 states by public-state CFR takes 3 minutes and 700 MB while a comparable version of vanilla CFR takes 5.5 hours and 20 GB. Additionally, the public-state formulation of CFR opens up the possibility for exploiting domain-specific assumptions, leading to a quadratic reduction in asymptotic complexity (and a further empirical speedup) over vanilla CFR in poker and other domains. Overall, this suggests that the ability to represent poker as a sequential Bayesian game played a key role in the success of CFR-based methods. Finally, we extend public-state CFR to general extensive-form games, arguing that this extension enjoys some - but not all - of the benefits of the version for sequential Bayesian games.

Is Truth-telling Favored in AI Debate?

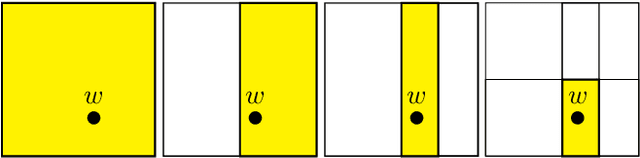
For some problems, humans may not be able to accurately judge the goodness of AI-proposed solutions. Irving et al. (2018) propose that in such cases, we may use a debate between two AI systems to amplify the problem-solving capabilities of a human judge. We introduce a mathematical framework that can model debates of this type and propose that the quality of debate designs should be measured by the accuracy of the most persuasive answer. We describe a simple instance of the debate framework called feature debate and analyze the degree to which such debates track the truth. We argue that despite being very simple, feature debates nonetheless capture many aspects of practical debates such as the incentives to confuse the judge or stall to prevent losing. We then outline how these models should be generalized to analyze a wider range of debate phenomena.

Rethinking Formal Models of Partially Observable Multiagent Decision Making

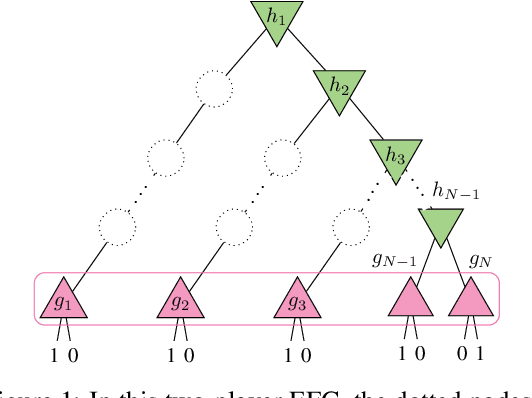
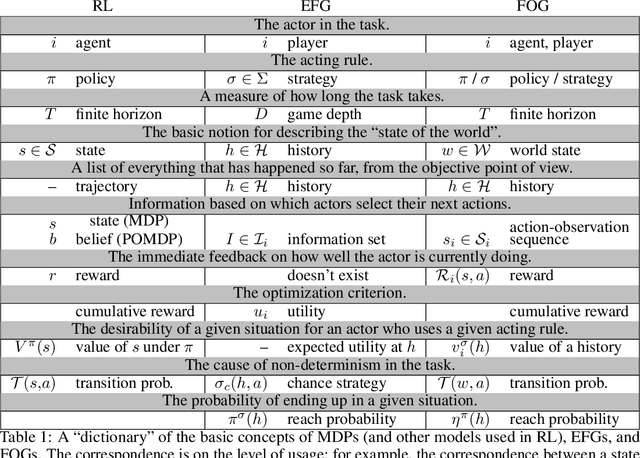
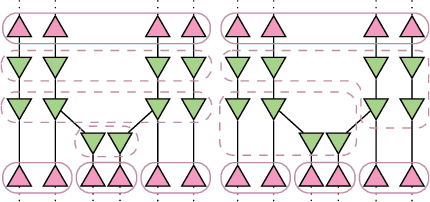
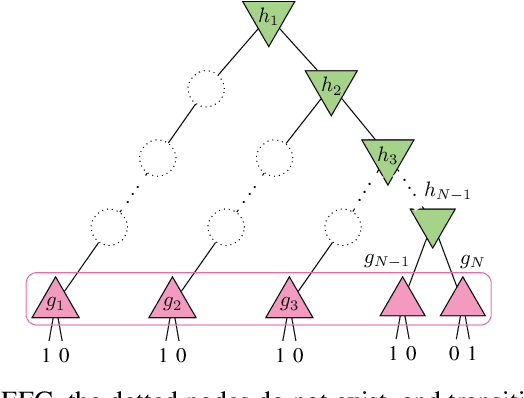
Multiagent decision-making problems in partially observable environments are usually modeled as either extensive-form games (EFGs) within the game theory community or partially observable stochastic games (POSGs) within the reinforcement learning community. While most practical problems can be modeled in both formalisms, the communities using these models are mostly distinct with little sharing of ideas or advances. The last decade has seen dramatic progress in algorithms for EFGs, mainly driven by the challenge problem of poker. We have seen computational techniques achieving super-human performance, some variants of poker are essentially solved, and there are now sound local search algorithms which were previously thought impossible. While the advances have garnered attention, the fundamental advances are not yet understood outside the EFG community. This can be largely explained by the starkly different formalisms between the game theory and reinforcement learning communities and, further, by the unsuitability of the original EFG formalism to make the ideas simple and clear. This paper aims to address these hindrances, by advocating a new unifying formalism, a variant of POSGs, which we call Factored-Observation Games (FOGs). We prove that any timeable perfect-recall EFG can be efficiently modeled as a FOG as well as relating FOGs to other existing formalisms. Additionally, a FOG explicitly identifies the public and private components of observations, which is fundamental to the recent EFG breakthroughs. We conclude by presenting the two building-blocks of these breakthroughs --- counterfactual regret minimization and public state decomposition --- in the new formalism, illustrating our goal of a simpler path for sharing recent advances between game theory and reinforcement learning community.