David Milec
Generation of Games for Opponent Model Differentiation
Nov 28, 2023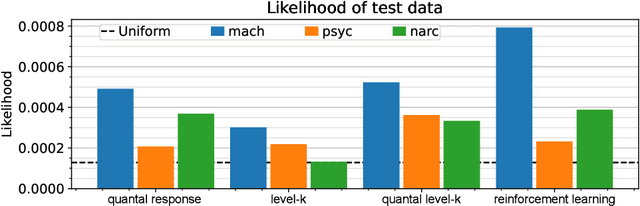

Abstract:Protecting against adversarial attacks is a common multiagent problem. Attackers in the real world are predominantly human actors, and the protection methods often incorporate opponent models to improve the performance when facing humans. Previous results show that modeling human behavior can significantly improve the performance of the algorithms. However, modeling humans correctly is a complex problem, and the models are often simplified and assume humans make mistakes according to some distribution or train parameters for the whole population from which they sample. In this work, we use data gathered by psychologists who identified personality types that increase the likelihood of performing malicious acts. However, in the previous work, the tests on a handmade game could not show strategic differences between the models. We created a novel model that links its parameters to psychological traits. We optimized over parametrized games and created games in which the differences are profound. Our work can help with automatic game generation when we need a game in which some models will behave differently and to identify situations in which the models do not align.
Fast Algorithms for Poker Require Modelling it as a Sequential Bayesian Game
Dec 20, 2021

Abstract:Many recent results in imperfect information games were only formulated for, or evaluated on, poker and poker-like games such as liar's dice. We argue that sequential Bayesian games constitute a natural class of games for generalizing these results. In particular, this model allows for an elegant formulation of the counterfactual regret minimization algorithm, called public-state CFR (PS-CFR), which naturally lends itself to an efficient implementation. Empirically, solving a poker subgame with 10^7 states by public-state CFR takes 3 minutes and 700 MB while a comparable version of vanilla CFR takes 5.5 hours and 20 GB. Additionally, the public-state formulation of CFR opens up the possibility for exploiting domain-specific assumptions, leading to a quadratic reduction in asymptotic complexity (and a further empirical speedup) over vanilla CFR in poker and other domains. Overall, this suggests that the ability to represent poker as a sequential Bayesian game played a key role in the success of CFR-based methods. Finally, we extend public-state CFR to general extensive-form games, arguing that this extension enjoys some - but not all - of the benefits of the version for sequential Bayesian games.
Complexity and Algorithms for Exploiting Quantal Opponents in Large Two-Player Games
Sep 30, 2020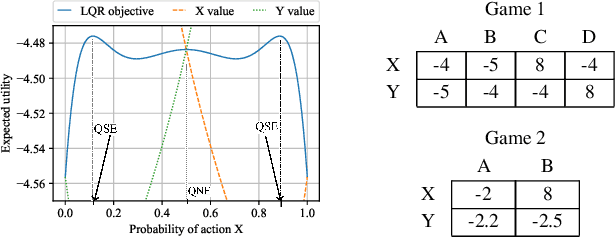
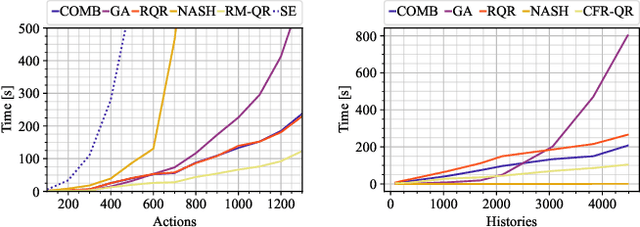
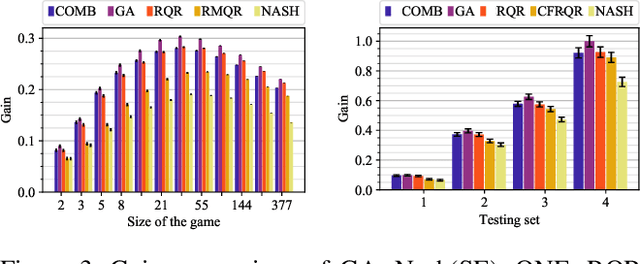
Abstract:Solution concepts of traditional game theory assume entirely rational players; therefore, their ability to exploit subrational opponents is limited. One type of subrationality that describes human behavior well is the quantal response. While there exist algorithms for computing solutions against quantal opponents, they either do not scale or may provide strategies that are even worse than the entirely-rational Nash strategies. This paper aims to analyze and propose scalable algorithms for computing effective and robust strategies against a quantal opponent in normal-form and extensive-form games. Our contributions are: (1) we define two different solution concepts related to exploiting quantal opponents and analyze their properties; (2) we prove that computing these solutions is computationally hard; (3) therefore, we evaluate several heuristic approximations based on scalable counterfactual regret minimization (CFR); and (4) we identify a CFR variant that exploits the bounded opponents better than the previously used variants while being less exploitable by the worst-case perfectly-rational opponent.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge