Plausible Counterfactual Explanations of Recommendations

Explanations play a variety of roles in various recommender systems, from a legally mandated afterthought, through an integral element of user experience, to a key to persuasiveness. A natural and useful form of an explanation is the Counterfactual Explanation (CE). We present a method for generating highly plausible CEs in recommender systems and evaluate it both numerically and with a user study.

Reducing Optimism Bias in Incomplete Cooperative Games

Cooperative game theory has diverse applications in contemporary artificial intelligence, including domains like interpretable machine learning, resource allocation, and collaborative decision-making. However, specifying a cooperative game entails assigning values to exponentially many coalitions, and obtaining even a single value can be resource-intensive in practice. Yet simply leaving certain coalition values undisclosed introduces ambiguity regarding individual contributions to the collective grand coalition. This ambiguity often leads to players holding overly optimistic expectations, stemming from either inherent biases or strategic considerations, frequently resulting in collective claims exceeding the actual grand coalition value. In this paper, we present a framework aimed at optimizing the sequence for revealing coalition values, with the overarching goal of efficiently closing the gap between players' expectations and achievable outcomes in cooperative games. Our contributions are threefold: (i) we study the individual players' optimistic completions of games with missing coalition values along with the arising gap, and investigate its analytical characteristics that facilitate more efficient optimization; (ii) we develop methods to minimize this gap over classes of games with a known prior by disclosing values of additional coalitions in both offline and online fashion; and (iii) we empirically demonstrate the algorithms' performance in practical scenarios, together with an investigation into the typical order of revealing coalition values.

Complexity and Algorithms for Exploiting Quantal Opponents in Large Two-Player Games

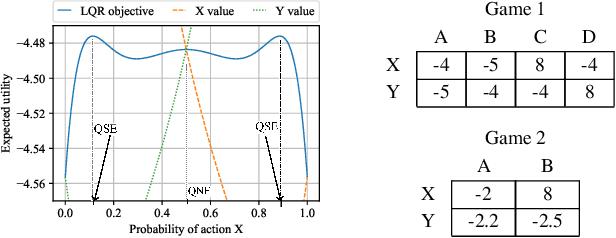
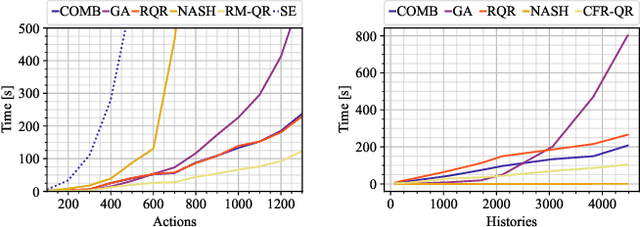
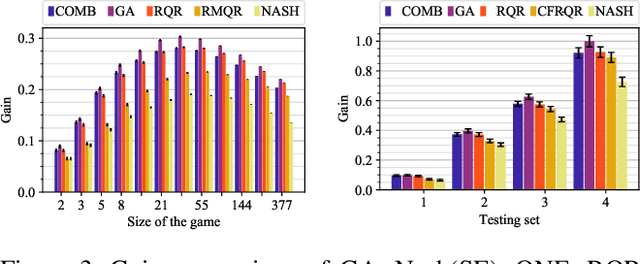
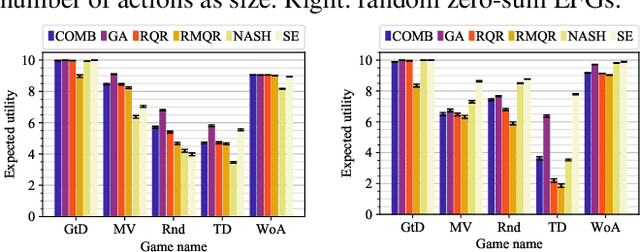
Solution concepts of traditional game theory assume entirely rational players; therefore, their ability to exploit subrational opponents is limited. One type of subrationality that describes human behavior well is the quantal response. While there exist algorithms for computing solutions against quantal opponents, they either do not scale or may provide strategies that are even worse than the entirely-rational Nash strategies. This paper aims to analyze and propose scalable algorithms for computing effective and robust strategies against a quantal opponent in normal-form and extensive-form games. Our contributions are: (1) we define two different solution concepts related to exploiting quantal opponents and analyze their properties; (2) we prove that computing these solutions is computationally hard; (3) therefore, we evaluate several heuristic approximations based on scalable counterfactual regret minimization (CFR); and (4) we identify a CFR variant that exploits the bounded opponents better than the previously used variants while being less exploitable by the worst-case perfectly-rational opponent.