Complexity and Algorithms for Exploiting Quantal Opponents in Large Two-Player Games
Paper and Code
Sep 30, 2020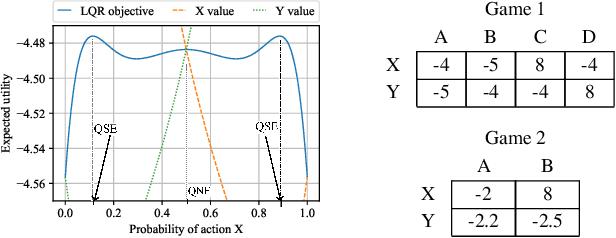
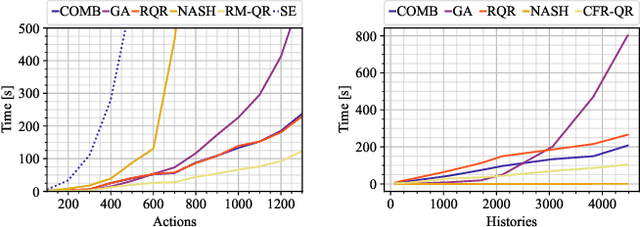
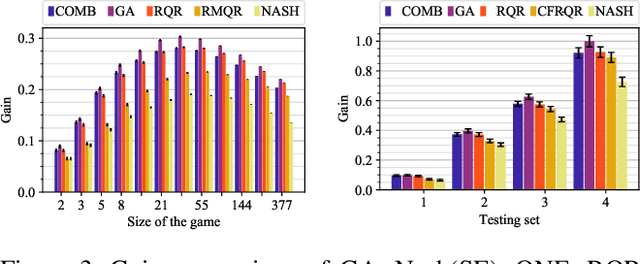
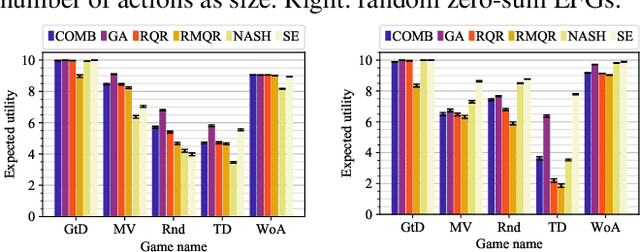
Solution concepts of traditional game theory assume entirely rational players; therefore, their ability to exploit subrational opponents is limited. One type of subrationality that describes human behavior well is the quantal response. While there exist algorithms for computing solutions against quantal opponents, they either do not scale or may provide strategies that are even worse than the entirely-rational Nash strategies. This paper aims to analyze and propose scalable algorithms for computing effective and robust strategies against a quantal opponent in normal-form and extensive-form games. Our contributions are: (1) we define two different solution concepts related to exploiting quantal opponents and analyze their properties; (2) we prove that computing these solutions is computationally hard; (3) therefore, we evaluate several heuristic approximations based on scalable counterfactual regret minimization (CFR); and (4) we identify a CFR variant that exploits the bounded opponents better than the previously used variants while being less exploitable by the worst-case perfectly-rational opponent.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge