A comparative analysis of rank aggregation methods for the partial label ranking problem

The label ranking problem is a supervised learning scenario in which the learner predicts a total order of the class labels for a given input instance. Recently, research has increasingly focused on the partial label ranking problem, a generalization of the label ranking problem that allows ties in the predicted orders. So far, most existing learning approaches for the partial label ranking problem rely on approximation algorithms for rank aggregation in the final prediction step. This paper explores several alternative aggregation methods for this critical step, including scoring-based and probabilistic-based rank aggregation approaches. To enhance their suitability for the more general partial label ranking problem, the investigated methods are extended to increase the likelihood of producing ties. Experimental evaluations on standard benchmarks demonstrate that scoring-based variants consistently outperform the current state-of-the-art method in handling incomplete information. In contrast, probabilistic-based variants fail to achieve competitive performance.

A calibration test for evaluating set-based epistemic uncertainty representations

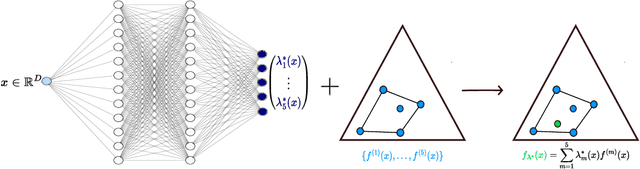
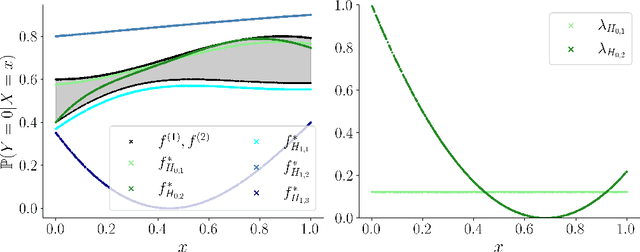
The accurate representation of epistemic uncertainty is a challenging yet essential task in machine learning. A widely used representation corresponds to convex sets of probabilistic predictors, also known as credal sets. One popular way of constructing these credal sets is via ensembling or specialized supervised learning methods, where the epistemic uncertainty can be quantified through measures such as the set size or the disagreement among members. In principle, these sets should contain the true data-generating distribution. As a necessary condition for this validity, we adopt the strongest notion of calibration as a proxy. Concretely, we propose a novel statistical test to determine whether there is a convex combination of the set's predictions that is calibrated in distribution. In contrast to previous methods, our framework allows the convex combination to be instance dependent, recognizing that different ensemble members may be better calibrated in different regions of the input space. Moreover, we learn this combination via proper scoring rules, which inherently optimize for calibration. Building on differentiable, kernel-based estimators of calibration errors, we introduce a nonparametric testing procedure and demonstrate the benefits of capturing instance-level variability on of synthetic and real-world experiments.

Is Epistemic Uncertainty Faithfully Represented by Evidential Deep Learning Methods?

Trustworthy ML systems should not only return accurate predictions, but also a reliable representation of their uncertainty. Bayesian methods are commonly used to quantify both aleatoric and epistemic uncertainty, but alternative approaches, such as evidential deep learning methods, have become popular in recent years. The latter group of methods in essence extends empirical risk minimization (ERM) for predicting second-order probability distributions over outcomes, from which measures of epistemic (and aleatoric) uncertainty can be extracted. This paper presents novel theoretical insights of evidential deep learning, highlighting the difficulties in optimizing second-order loss functions and interpreting the resulting epistemic uncertainty measures. With a systematic setup that covers a wide range of approaches for classification, regression and counts, it provides novel insights into issues of identifiability and convergence in second-order loss minimization, and the relative (rather than absolute) nature of epistemic uncertainty measures.

A Survey of Reinforcement Learning from Human Feedback

Reinforcement learning from human feedback (RLHF) is a variant of reinforcement learning (RL) that learns from human feedback instead of relying on an engineered reward function. Building on prior work on the related setting of preference-based reinforcement learning (PbRL), it stands at the intersection of artificial intelligence and human-computer interaction. This positioning offers a promising avenue to enhance the performance and adaptability of intelligent systems while also improving the alignment of their objectives with human values. The training of Large Language Models (LLMs) has impressively demonstrated this potential in recent years, where RLHF played a decisive role in targeting the model's capabilities toward human objectives. This article provides a comprehensive overview of the fundamentals of RLHF, exploring the intricate dynamics between machine agents and human input. While recent focus has been on RLHF for LLMs, our survey adopts a broader perspective, examining the diverse applications and wide-ranging impact of the technique. We delve into the core principles that underpin RLHF, shedding light on the symbiotic relationship between algorithms and human feedback, and discuss the main research trends in the field. By synthesizing the current landscape of RLHF research, this article aims to provide researchers as well as practitioners with a comprehensive understanding of this rapidly growing field of research.

Second-Order Uncertainty Quantification: A Distance-Based Approach

In the past couple of years, various approaches to representing and quantifying different types of predictive uncertainty in machine learning, notably in the setting of classification, have been proposed on the basis of second-order probability distributions, i.e., predictions in the form of distributions on probability distributions. A completely conclusive solution has not yet been found, however, as shown by recent criticisms of commonly used uncertainty measures associated with second-order distributions, identifying undesirable theoretical properties of these measures. In light of these criticisms, we propose a set of formal criteria that meaningful uncertainty measures for predictive uncertainty based on second-order distributions should obey. Moreover, we provide a general framework for developing uncertainty measures to account for these criteria, and offer an instantiation based on the Wasserstein distance, for which we prove that all criteria are satisfied.

Identifying Copeland Winners in Dueling Bandits with Indifferences

We consider the task of identifying the Copeland winner(s) in a dueling bandits problem with ternary feedback. This is an underexplored but practically relevant variant of the conventional dueling bandits problem, in which, in addition to strict preference between two arms, one may observe feedback in the form of an indifference. We provide a lower bound on the sample complexity for any learning algorithm finding the Copeland winner(s) with a fixed error probability. Moreover, we propose POCOWISTA, an algorithm with a sample complexity that almost matches this lower bound, and which shows excellent empirical performance, even for the conventional dueling bandits problem. For the case where the preference probabilities satisfy a specific type of stochastic transitivity, we provide a refined version with an improved worst case sample complexity.

Iterative Deepening Hyperband

Hyperparameter optimization (HPO) is concerned with the automated search for the most appropriate hyperparameter configuration (HPC) of a parameterized machine learning algorithm. A state-of-the-art HPO method is Hyperband, which, however, has its own parameters that influence its performance. One of these parameters, the maximal budget, is especially problematic: If chosen too small, the budget needs to be increased in hindsight and, as Hyperband is not incremental by design, the entire algorithm must be re-run. This is not only costly but also comes with a loss of valuable knowledge already accumulated. In this paper, we propose incremental variants of Hyperband that eliminate these drawbacks, and show that these variants satisfy theoretical guarantees qualitatively similar to those for the original Hyperband with the "right" budget. Moreover, we demonstrate their practical utility in experiments with benchmark data sets.

Approximating the Shapley Value without Marginal Contributions

The Shapley value is arguably the most popular approach for assigning a meaningful contribution value to players in a cooperative game, which has recently been used intensively in various areas of machine learning, most notably in explainable artificial intelligence. The meaningfulness is due to axiomatic properties that only the Shapley value satisfies, which, however, comes at the expense of an exact computation growing exponentially with the number of agents. Accordingly, a number of works are devoted to the efficient approximation of the Shapley values, all of which revolve around the notion of an agent's marginal contribution. In this paper, we propose with SVARM and Stratified SVARM two parameter-free and domain-independent approximation algorithms based on a representation of the Shapley value detached from the notion of marginal contributions. We prove unmatched theoretical guarantees regarding their approximation quality and provide satisfying empirical results.

On Second-Order Scoring Rules for Epistemic Uncertainty Quantification

It is well known that accurate probabilistic predictors can be trained through empirical risk minimisation with proper scoring rules as loss functions. While such learners capture so-called aleatoric uncertainty of predictions, various machine learning methods have recently been developed with the goal to let the learner also represent its epistemic uncertainty, i.e., the uncertainty caused by a lack of knowledge and data. An emerging branch of the literature proposes the use of a second-order learner that provides predictions in terms of distributions on probability distributions. However, recent work has revealed serious theoretical shortcomings for second-order predictors based on loss minimisation. In this paper, we generalise these findings and prove a more fundamental result: There seems to be no loss function that provides an incentive for a second-order learner to faithfully represent its epistemic uncertainty in the same manner as proper scoring rules do for standard (first-order) learners. As a main mathematical tool to prove this result, we introduce the generalised notion of second-order scoring rules.

AC-Band: A Combinatorial Bandit-Based Approach to Algorithm Configuration

We study the algorithm configuration (AC) problem, in which one seeks to find an optimal parameter configuration of a given target algorithm in an automated way. Recently, there has been significant progress in designing AC approaches that satisfy strong theoretical guarantees. However, a significant gap still remains between the practical performance of these approaches and state-of-the-art heuristic methods. To this end, we introduce AC-Band, a general approach for the AC problem based on multi-armed bandits that provides theoretical guarantees while exhibiting strong practical performance. We show that AC-Band requires significantly less computation time than other AC approaches providing theoretical guarantees while still yielding high-quality configurations.