Shapley Value Approximation Based on k-Additive Games

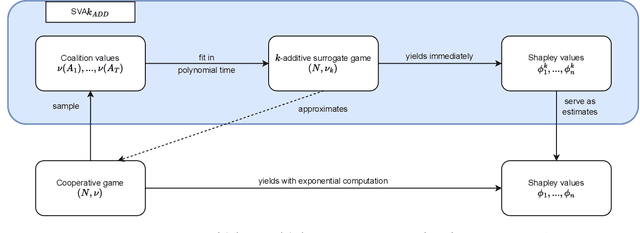
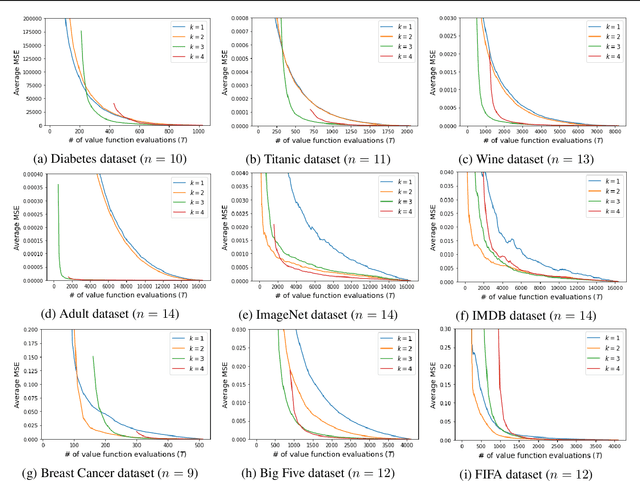
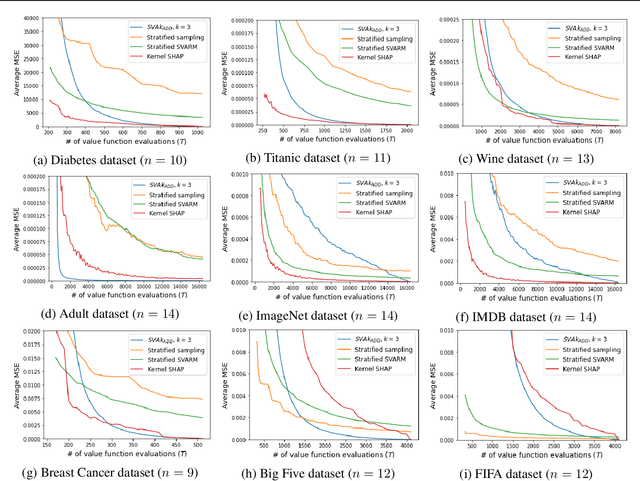
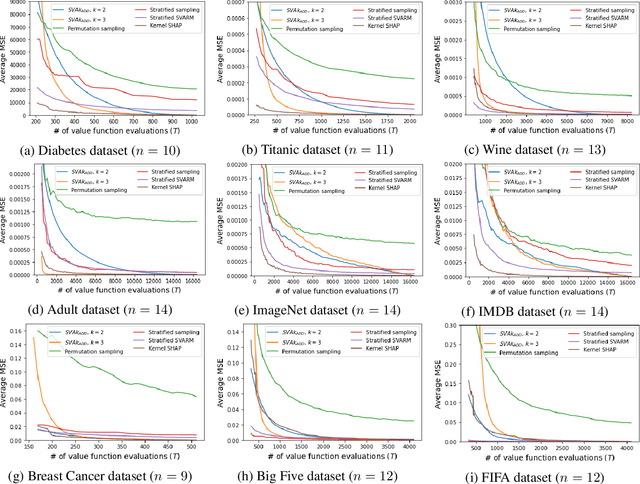
The Shapley value is the prevalent solution for fair division problems in which a payout is to be divided among multiple agents. By adopting a game-theoretic view, the idea of fair division and the Shapley value can also be used in machine learning to quantify the individual contribution of features or data points to the performance of a predictive model. Despite its popularity and axiomatic justification, the Shapley value suffers from a computational complexity that scales exponentially with the number of entities involved, and hence requires approximation methods for its reliable estimation. We propose SVA$k_{\text{ADD}}$, a novel approximation method that fits a $k$-additive surrogate game. By taking advantage of $k$-additivity, we are able to elicit the exact Shapley values of the surrogate game and then use these values as estimates for the original fair division problem. The efficacy of our method is evaluated empirically and compared to competing methods.

shapiq: Shapley Interactions for Machine Learning

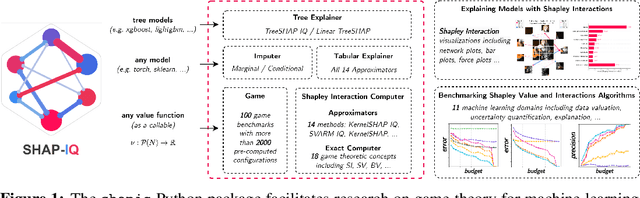
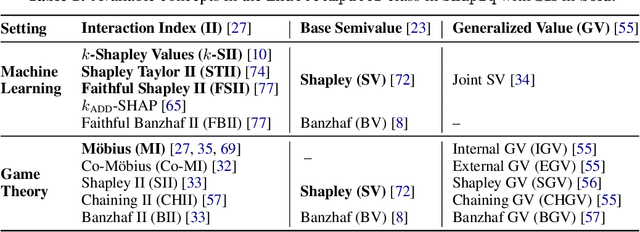
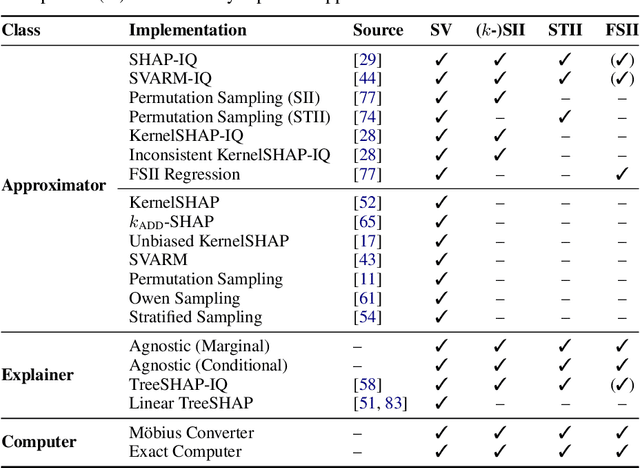
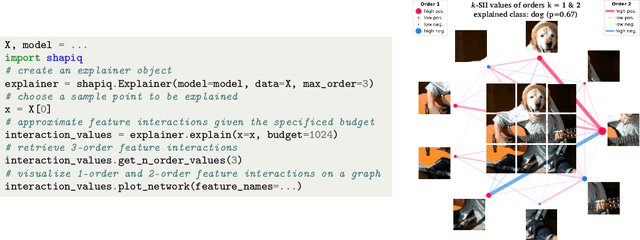
Originally rooted in game theory, the Shapley Value (SV) has recently become an important tool in machine learning research. Perhaps most notably, it is used for feature attribution and data valuation in explainable artificial intelligence. Shapley Interactions (SIs) naturally extend the SV and address its limitations by assigning joint contributions to groups of entities, which enhance understanding of black box machine learning models. Due to the exponential complexity of computing SVs and SIs, various methods have been proposed that exploit structural assumptions or yield probabilistic estimates given limited resources. In this work, we introduce shapiq, an open-source Python package that unifies state-of-the-art algorithms to efficiently compute SVs and any-order SIs in an application-agnostic framework. Moreover, it includes a benchmarking suite containing 11 machine learning applications of SIs with pre-computed games and ground-truth values to systematically assess computational performance across domains. For practitioners, shapiq is able to explain and visualize any-order feature interactions in predictions of models, including vision transformers, language models, as well as XGBoost and LightGBM with TreeSHAP-IQ. With shapiq, we extend shap beyond feature attributions and consolidate the application of SVs and SIs in machine learning that facilitates future research. The source code and documentation are available at https://github.com/mmschlk/shapiq.

KernelSHAP-IQ: Weighted Least-Square Optimization for Shapley Interactions

The Shapley value (SV) is a prevalent approach of allocating credit to machine learning (ML) entities to understand black box ML models. Enriching such interpretations with higher-order interactions is inevitable for complex systems, where the Shapley Interaction Index (SII) is a direct axiomatic extension of the SV. While it is well-known that the SV yields an optimal approximation of any game via a weighted least square (WLS) objective, an extension of this result to SII has been a long-standing open problem, which even led to the proposal of an alternative index. In this work, we characterize higher-order SII as a solution to a WLS problem, which constructs an optimal approximation via SII and $k$-Shapley values ($k$-SII). We prove this representation for the SV and pairwise SII and give empirically validated conjectures for higher orders. As a result, we propose KernelSHAP-IQ, a direct extension of KernelSHAP for SII, and demonstrate state-of-the-art performance for feature interactions.

SHAP-IQ: Unified Approximation of any-order Shapley Interactions

Predominately in explainable artificial intelligence (XAI) research, the Shapley value (SV) is applied to determine feature importance scores for any black box model. Shapley interaction indices extend the Shapley value to define any-order feature interaction scores. Defining a unique Shapley interaction index is an open research question and, so far, three definitions have been proposed, which differ by their choice of axioms. Moreover, each definition requires a specific approximation technique. We, however, propose SHAPley Interaction Quantification (SHAP-IQ), an efficient sampling-based approximator to compute Shapley interactions for all three definitions, as well as all other that satisfy the linearity, symmetry and dummy axiom. SHAP-IQ is based on a novel representation and, in contrast to existing methods, we provide theoretical guarantees for its approximation quality, as well as estimates for the variance of the point estimates. For the special case of SV, our approach reveals a novel representation of the SV and corresponds to Unbiased KernelSHAP with a greatly simplified calculation. We illustrate the computational efficiency and effectiveness by explaining state-of-the-art language models among high-dimensional synthetic models.

Approximating the Shapley Value without Marginal Contributions

The Shapley value is arguably the most popular approach for assigning a meaningful contribution value to players in a cooperative game, which has recently been used intensively in various areas of machine learning, most notably in explainable artificial intelligence. The meaningfulness is due to axiomatic properties that only the Shapley value satisfies, which, however, comes at the expense of an exact computation growing exponentially with the number of agents. Accordingly, a number of works are devoted to the efficient approximation of the Shapley values, all of which revolve around the notion of an agent's marginal contribution. In this paper, we propose with SVARM and Stratified SVARM two parameter-free and domain-independent approximation algorithms based on a representation of the Shapley value detached from the notion of marginal contributions. We prove unmatched theoretical guarantees regarding their approximation quality and provide satisfying empirical results.

Non-Stationary Dueling Bandits

We study the non-stationary dueling bandits problem with $K$ arms, where the time horizon $T$ consists of $M$ stationary segments, each of which is associated with its own preference matrix. The learner repeatedly selects a pair of arms and observes a binary preference between them as feedback. To minimize the accumulated regret, the learner needs to pick the Condorcet winner of each stationary segment as often as possible, despite preference matrices and segment lengths being unknown. We propose the $\mathrm{Beat\, the\, Winner\, Reset}$ algorithm and prove a bound on its expected binary weak regret in the stationary case, which tightens the bound of current state-of-art algorithms. We also show a regret bound for the non-stationary case, without requiring knowledge of $M$ or $T$. We further propose and analyze two meta-algorithms, $\mathrm{DETECT}$ for weak regret and $\mathrm{Monitored\, Dueling\, Bandits}$ for strong regret, both based on a detection-window approach that can incorporate any dueling bandit algorithm as a black-box algorithm. Finally, we prove a worst-case lower bound for expected weak regret in the non-stationary case.