A statistical approach to detect sensitive features in a group fairness setting

The use of machine learning models in decision support systems with high societal impact raised concerns about unfair (disparate) results for different groups of people. When evaluating such unfair decisions, one generally relies on predefined groups that are determined by a set of features that are considered sensitive. However, such an approach is subjective and does not guarantee that these features are the only ones to be considered as sensitive nor that they entail unfair (disparate) outcomes. In this paper, we propose a preprocessing step to address the task of automatically recognizing sensitive features that does not require a trained model to verify unfair results. Our proposal is based on the Hilber-Schmidt independence criterion, which measures the statistical dependence of variable distributions. We hypothesize that if the dependence between the label vector and a candidate is high for a sensitive feature, then the information provided by this feature will entail disparate performance measures between groups. Our empirical results attest our hypothesis and show that several features considered as sensitive in the literature do not necessarily entail disparate (unfair) results.

A $k$-additive Choquet integral-based approach to approximate the SHAP values for local interpretability in machine learning

Besides accuracy, recent studies on machine learning models have been addressing the question on how the obtained results can be interpreted. Indeed, while complex machine learning models are able to provide very good results in terms of accuracy even in challenging applications, it is difficult to interpret them. Aiming at providing some interpretability for such models, one of the most famous methods, called SHAP, borrows the Shapley value concept from game theory in order to locally explain the predicted outcome of an instance of interest. As the SHAP values calculation needs previous computations on all possible coalitions of attributes, its computational cost can be very high. Therefore, a SHAP-based method called Kernel SHAP adopts an efficient strategy that approximate such values with less computational effort. In this paper, we also address local interpretability in machine learning based on Shapley values. Firstly, we provide a straightforward formulation of a SHAP-based method for local interpretability by using the Choquet integral, which leads to both Shapley values and Shapley interaction indices. Moreover, we also adopt the concept of $k$-additive games from game theory, which contributes to reduce the computational effort when estimating the SHAP values. The obtained results attest that our proposal needs less computations on coalitions of attributes to approximate the SHAP values.

Shapley value-based approaches to explain the robustness of classifiers in machine learning

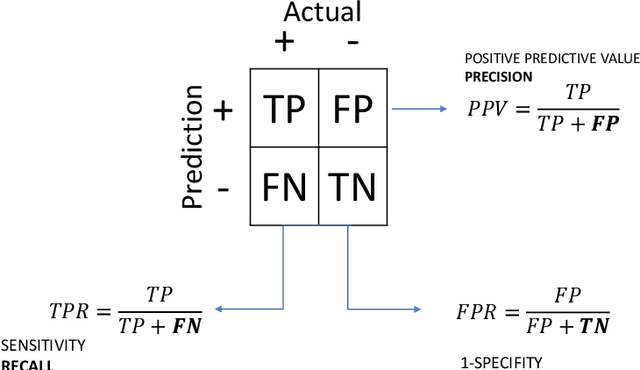
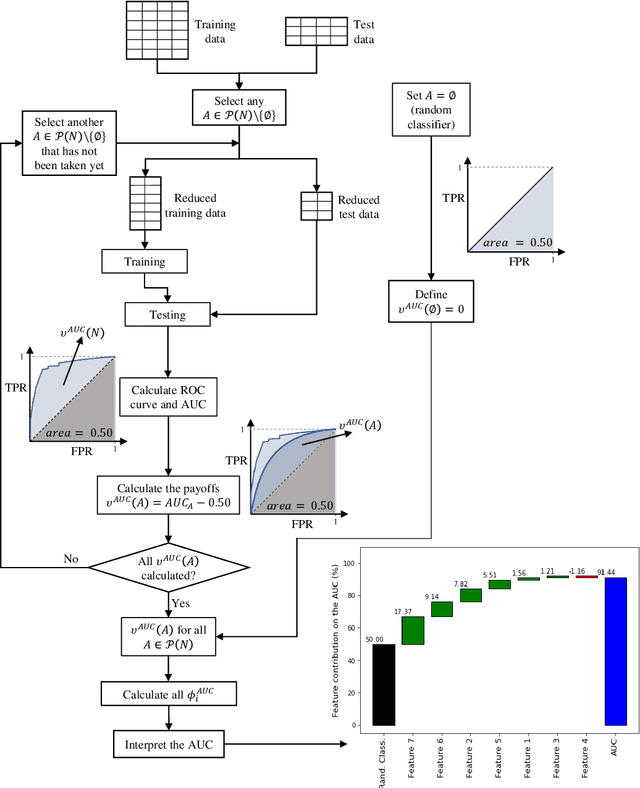
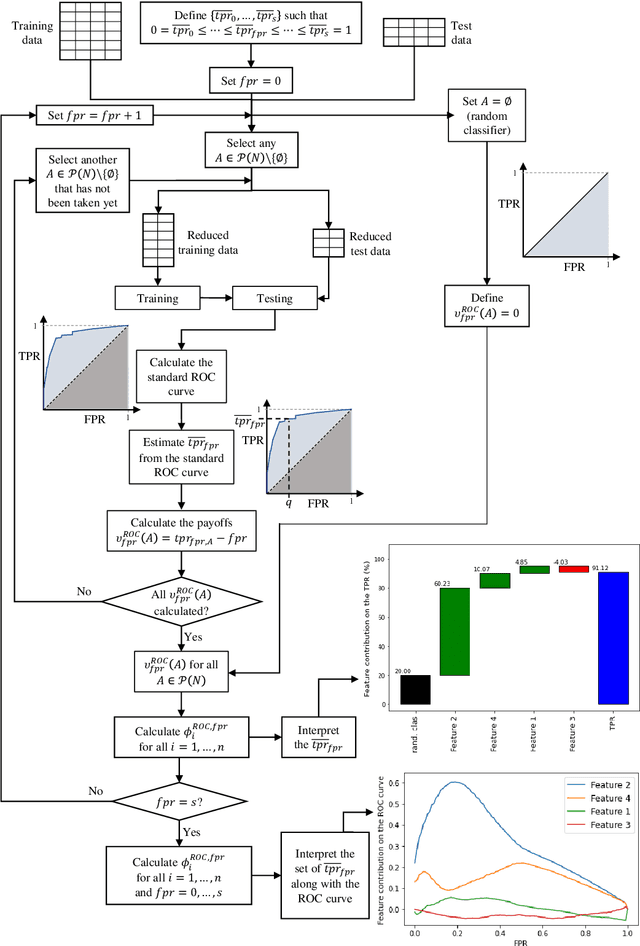
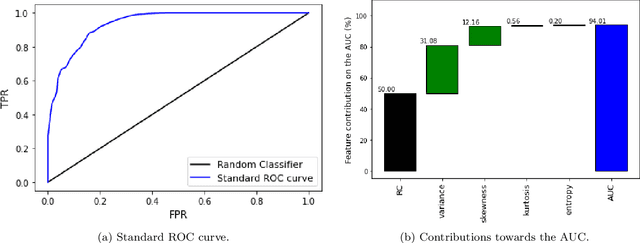
In machine learning, the use of algorithm-agnostic approaches is an emerging area of research for explaining the contribution of individual features towards the predicted outcome. Whilst there is a focus on explaining the prediction itself, a little has been done on explaining the robustness of these models, that is, how each feature contributes towards achieving that robustness. In this paper, we propose the use of Shapley values to explain the contribution of each feature towards the model's robustness, measured in terms of Receiver-operating Characteristics (ROC) curve and the Area under the ROC curve (AUC). With the help of an illustrative example, we demonstrate the proposed idea of explaining the ROC curve, and visualising the uncertainties in these curves. For imbalanced datasets, the use of Precision-Recall Curve (PRC) is considered more appropriate, therefore we also demonstrate how to explain the PRCs with the help of Shapley values.

A novel approach for Fair Principal Component Analysis based on eigendecomposition

Principal component analysis (PCA), a ubiquitous dimensionality reduction technique in signal processing, searches for a projection matrix that minimizes the mean squared error between the reduced dataset and the original one. Since classical PCA is not tailored to address concerns related to fairness, its application to actual problems may lead to disparity in the reconstruction errors of different groups (e.g., men and women, whites and blacks, etc.), with potentially harmful consequences such as the introduction of bias towards sensitive groups. Although several fair versions of PCA have been proposed recently, there still remains a fundamental gap in the search for algorithms that are simple enough to be deployed in real systems. To address this, we propose a novel PCA algorithm which tackles fairness issues by means of a simple strategy comprising a one-dimensional search which exploits the closed-form solution of PCA. As attested by numerical experiments, the proposal can significantly improve fairness with a very small loss in the overall reconstruction error and without resorting to complex optimization schemes. Moreover, our findings are consistent in several real situations as well as in scenarios with both unbalanced and balanced datasets.

Application of independent component analysis and TOPSIS to deal with dependent criteria in multicriteria decision problems

A vast number of multicriteria decision making methods have been developed to deal with the problem of ranking a set of alternatives evaluated in a multicriteria fashion. Very often, these methods assume that the evaluation among criteria is statistically independent. However, in actual problems, the observed data may comprise dependent criteria, which, among other problems, may result in biased rankings. In order to deal with this issue, we propose a novel approach whose aim is to estimate, from the observed data, a set of independent latent criteria, which can be seen as an alternative representation of the original decision matrix. A central element of our approach is to formulate the decision problem as a blind source separation problem, which allows us to apply independent component analysis techniques to estimate the latent criteria. Moreover, we consider TOPSIS-based approaches to obtain the ranking of alternatives from the latent criteria. Results in both synthetic and actual data attest the relevance of the proposed approach.