A calibration test for evaluating set-based epistemic uncertainty representations

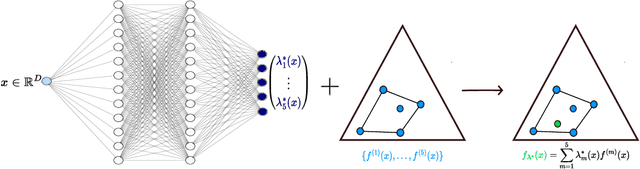
The accurate representation of epistemic uncertainty is a challenging yet essential task in machine learning. A widely used representation corresponds to convex sets of probabilistic predictors, also known as credal sets. One popular way of constructing these credal sets is via ensembling or specialized supervised learning methods, where the epistemic uncertainty can be quantified through measures such as the set size or the disagreement among members. In principle, these sets should contain the true data-generating distribution. As a necessary condition for this validity, we adopt the strongest notion of calibration as a proxy. Concretely, we propose a novel statistical test to determine whether there is a convex combination of the set's predictions that is calibrated in distribution. In contrast to previous methods, our framework allows the convex combination to be instance dependent, recognizing that different ensemble members may be better calibrated in different regions of the input space. Moreover, we learn this combination via proper scoring rules, which inherently optimize for calibration. Building on differentiable, kernel-based estimators of calibration errors, we introduce a nonparametric testing procedure and demonstrate the benefits of capturing instance-level variability on of synthetic and real-world experiments.

Chasing the Timber Trail: Machine Learning to Reveal Harvest Location Misrepresentation

Illegal logging poses a significant threat to global biodiversity, climate stability, and depresses international prices for legal wood harvesting and responsible forest products trade, affecting livelihoods and communities across the globe. Stable isotope ratio analysis (SIRA) is rapidly becoming an important tool for determining the harvest location of traded, organic, products. The spatial pattern in stable isotope ratio values depends on factors such as atmospheric and environmental conditions and can thus be used for geographical identification. We present here the results of a deployed machine learning pipeline where we leverage both isotope values and atmospheric variables to determine timber harvest location. Additionally, the pipeline incorporates uncertainty estimation to facilitate the interpretation of harvest location determination for analysts. We present our experiments on a collection of oak (Quercus spp.) tree samples from its global range. Our pipeline outperforms comparable state-of-the-art models determining geographic harvest origin of commercially traded wood products, and has been used by European enforcement agencies to identify illicit Russian and Belarusian timber entering the EU market. We also identify opportunities for further advancement of our framework and how it can be generalized to help identify the origin of falsely labeled organic products throughout the supply chain.

Conformal Prediction in Hierarchical Classification

Conformal prediction has emerged as a widely used framework for constructing valid prediction sets in classification and regression tasks. In this work, we extend the split conformal prediction framework to hierarchical classification, where prediction sets are commonly restricted to internal nodes of a predefined hierarchy, and propose two computationally efficient inference algorithms. The first algorithm returns internal nodes as prediction sets, while the second relaxes this restriction, using the notion of representation complexity, yielding a more general and combinatorial inference problem, but smaller set sizes. Empirical evaluations on several benchmark datasets demonstrate the effectiveness of the proposed algorithms in achieving nominal coverage.

On Calibration of Ensemble-Based Credal Predictors

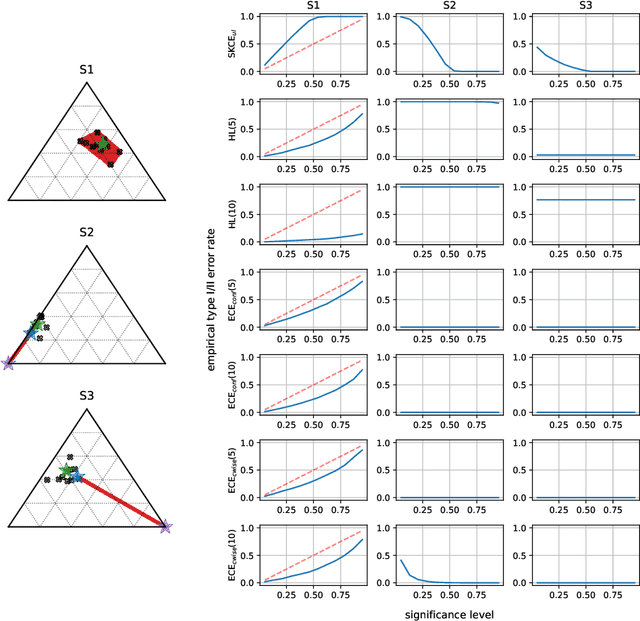
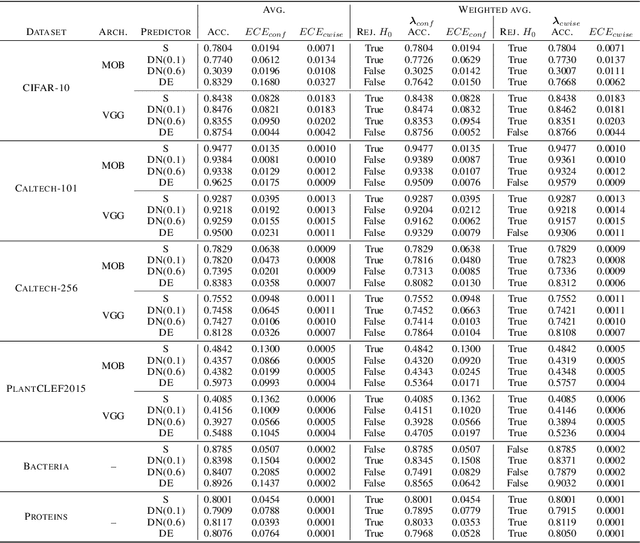
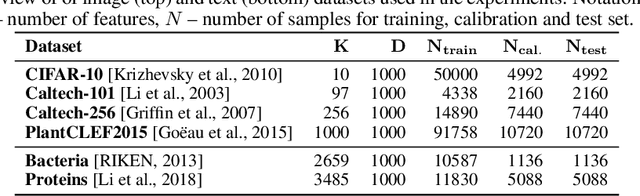
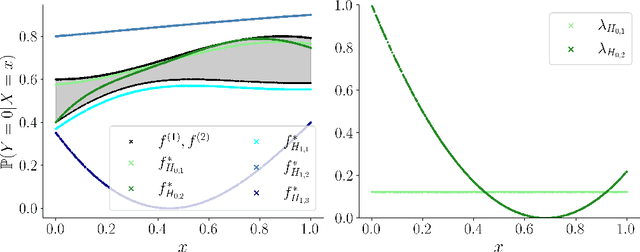
In recent years, several classification methods that intend to quantify epistemic uncertainty have been proposed, either by producing predictions in the form of second-order distributions or sets of probability distributions. In this work, we focus on the latter, also called credal predictors, and address the question of how to evaluate them: What does it mean that a credal predictor represents epistemic uncertainty in a faithful manner? To answer this question, we refer to the notion of calibration of probabilistic predictors and extend it to credal predictors. Broadly speaking, we call a credal predictor calibrated if it returns sets that cover the true conditional probability distribution. To verify this property for the important case of ensemble-based credal predictors, we propose a novel nonparametric calibration test that generalizes an existing test for probabilistic predictors to the case of credal predictors. Making use of this test, we empirically show that credal predictors based on deep neural networks are often not well calibrated.

Set-valued prediction in hierarchical classification with constrained representation complexity

Set-valued prediction is a well-known concept in multi-class classification. When a classifier is uncertain about the class label for a test instance, it can predict a set of classes instead of a single class. In this paper, we focus on hierarchical multi-class classification problems, where valid sets (typically) correspond to internal nodes of the hierarchy. We argue that this is a very strong restriction, and we propose a relaxation by introducing the notion of representation complexity for a predicted set. In combination with probabilistic classifiers, this leads to a challenging inference problem for which specific combinatorial optimization algorithms are needed. We propose three methods and evaluate them on benchmark datasets: a na\"ive approach that is based on matrix-vector multiplication, a reformulation as a knapsack problem with conflict graph, and a recursive tree search method. Experimental results demonstrate that the last method is computationally more efficient than the other two approaches, due to a hierarchical factorization of the conditional class distribution.

Efficient Algorithms for Set-Valued Prediction in Multi-Class Classification

In cases of uncertainty, a multi-class classifier preferably returns a set of candidate classes instead of predicting a single class label with little guarantee. More precisely, the classifier should strive for an optimal balance between the correctness (the true class is among the candidates) and the precision (the candidates are not too many) of its prediction. We formalize this problem within a general decision-theoretic framework that unifies most of the existing work in this area. In this framework, uncertainty is quantified in terms of conditional class probabilities, and the quality of a predicted set is measured in terms of a utility function. We then address the problem of finding the Bayes-optimal prediction, i.e., the subset of class labels with highest expected utility. For this problem, which is computationally challenging as there are exponentially (in the number of classes) many predictions to choose from, we propose efficient algorithms that can be applied to a broad family of utility scores. Two of these algorithms make use of structural information in the form of a class hierarchy, which is often available in prediction problems with many classes. Our theoretical results are complemented by experimental studies, in which we analyze the proposed algorithms in terms of predictive accuracy and runtime efficiency.