Constraint-Guided Learning of Data-driven Health Indicator Models: An Application on the Pronostia Bearing Dataset

This paper presents a constraint-guided deep learning framework for developing physically consistent health indicators in bearing prognostics and health management. Conventional data-driven methods often lack physical plausibility, while physics-based models are limited by incomplete system knowledge. To address this, we integrate domain knowledge into deep learning using constraints to enforce monotonicity, bound output values between 1 and 0 (representing healthy to failed states), and ensure consistency between signal energy trends and health indicator estimates. This eliminates the need for complex loss term balancing. We implement constraint-guided gradient descent within an autoencoder architecture, creating a constrained autoencoder. However, the framework is adaptable to other architectures. Using time-frequency representations of accelerometer signals from the Pronostia dataset, our constrained model generates smoother, more reliable degradation profiles compared to conventional methods, aligning with expected physical behavior. Performance is assessed using three metrics: trendability, robustness, and consistency. Compared to a conventional baseline, the constrained model improves all three. Another baseline, incorporating monotonicity via a soft-ranking loss function, outperforms in trendability but falls short in robustness and consistency. An ablation study confirms that the monotonicity constraint enhances trendability, the boundary constraint ensures consistency, and the energy-health consistency constraint improves robustness. These findings highlight the effectiveness of constraint-guided deep learning in producing reliable, physically meaningful health indicators, offering a promising direction for future prognostic applications.

On Calibration of Ensemble-Based Credal Predictors

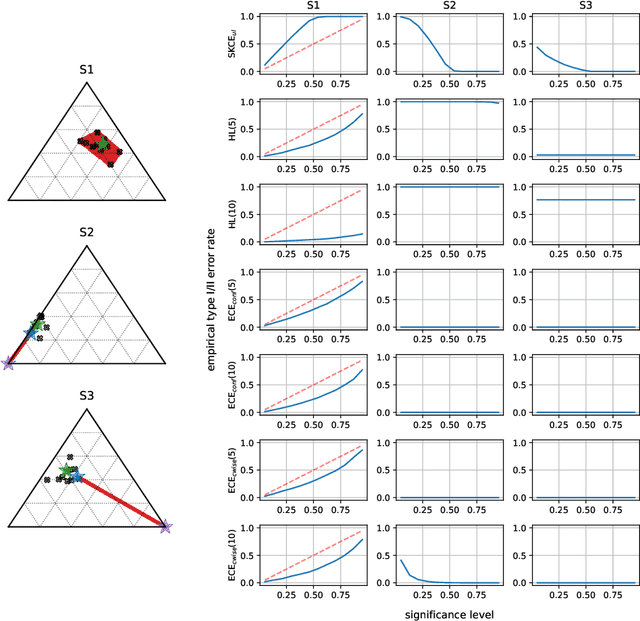
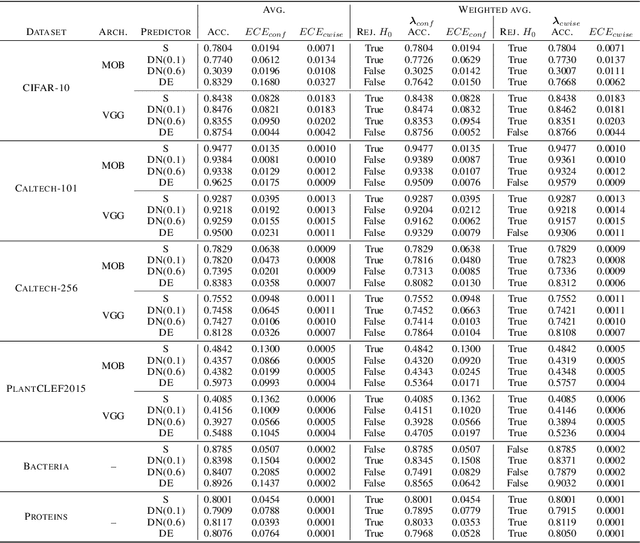
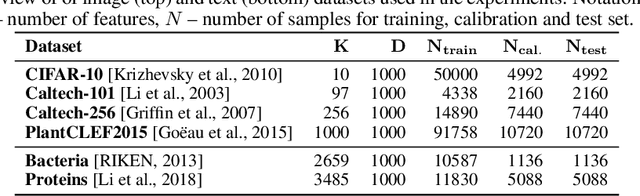
In recent years, several classification methods that intend to quantify epistemic uncertainty have been proposed, either by producing predictions in the form of second-order distributions or sets of probability distributions. In this work, we focus on the latter, also called credal predictors, and address the question of how to evaluate them: What does it mean that a credal predictor represents epistemic uncertainty in a faithful manner? To answer this question, we refer to the notion of calibration of probabilistic predictors and extend it to credal predictors. Broadly speaking, we call a credal predictor calibrated if it returns sets that cover the true conditional probability distribution. To verify this property for the important case of ensemble-based credal predictors, we propose a novel nonparametric calibration test that generalizes an existing test for probabilistic predictors to the case of credal predictors. Making use of this test, we empirically show that credal predictors based on deep neural networks are often not well calibrated.