NeTO:Neural Reconstruction of Transparent Objects with Self-Occlusion Aware Refraction-Tracing

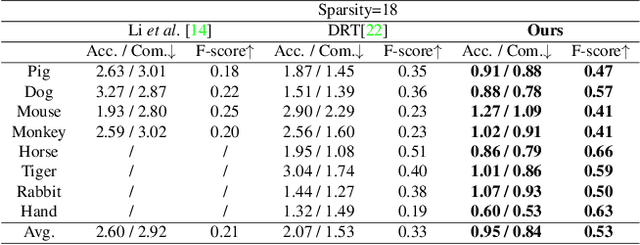
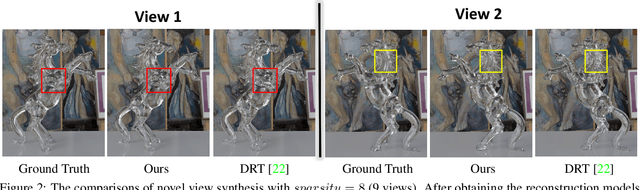
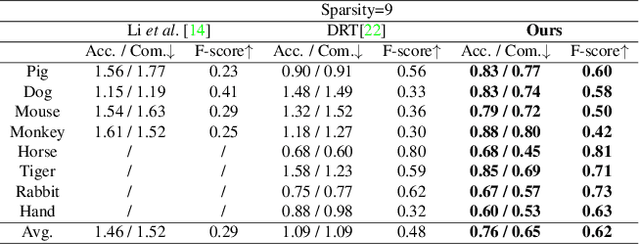
We present a novel method, called NeTO, for capturing 3D geometry of solid transparent objects from 2D images via volume rendering. Reconstructing transparent objects is a very challenging task, which is ill-suited for general-purpose reconstruction techniques due to the specular light transport phenomena. Although existing refraction-tracing based methods, designed specially for this task, achieve impressive results, they still suffer from unstable optimization and loss of fine details, since the explicit surface representation they adopted is difficult to be optimized, and the self-occlusion problem is ignored for refraction-tracing. In this paper, we propose to leverage implicit Signed Distance Function (SDF) as surface representation, and optimize the SDF field via volume rendering with a self-occlusion aware refractive ray tracing. The implicit representation enables our method to be capable of reconstructing high-quality reconstruction even with a limited set of images, and the self-occlusion aware strategy makes it possible for our method to accurately reconstruct the self-occluded regions. Experiments show that our method achieves faithful reconstruction results and outperforms prior works by a large margin. Visit our project page at \url{https://www.xxlong.site/NeTO/}

NeuralRoom: Geometry-Constrained Neural Implicit Surfaces for Indoor Scene Reconstruction

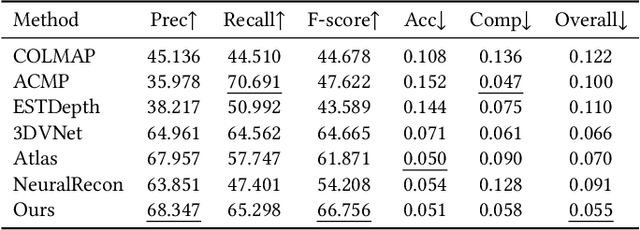
We present a novel neural surface reconstruction method called NeuralRoom for reconstructing room-sized indoor scenes directly from a set of 2D images. Recently, implicit neural representations have become a promising way to reconstruct surfaces from multiview images due to their high-quality results and simplicity. However, implicit neural representations usually cannot reconstruct indoor scenes well because they suffer severe shape-radiance ambiguity. We assume that the indoor scene consists of texture-rich and flat texture-less regions. In texture-rich regions, the multiview stereo can obtain accurate results. In the flat area, normal estimation networks usually obtain a good normal estimation. Based on the above observations, we reduce the possible spatial variation range of implicit neural surfaces by reliable geometric priors to alleviate shape-radiance ambiguity. Specifically, we use multiview stereo results to limit the NeuralRoom optimization space and then use reliable geometric priors to guide NeuralRoom training. Then the NeuralRoom would produce a neural scene representation that can render an image consistent with the input training images. In addition, we propose a smoothing method called perturbation-residual restrictions to improve the accuracy and completeness of the flat region, which assumes that the sampling points in a local surface should have the same normal and similar distance to the observation center. Experiments on the ScanNet dataset show that our method can reconstruct the texture-less area of indoor scenes while maintaining the accuracy of detail. We also apply NeuralRoom to more advanced multiview reconstruction algorithms and significantly improve their reconstruction quality.

DGECN: A Depth-Guided Edge Convolutional Network for End-to-End 6D Pose Estimation

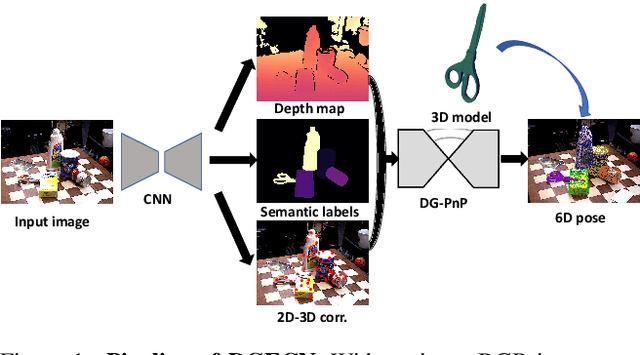
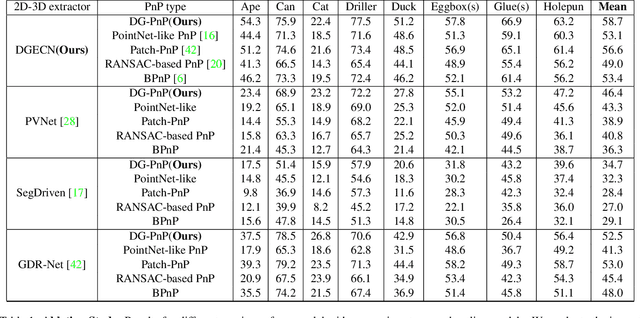
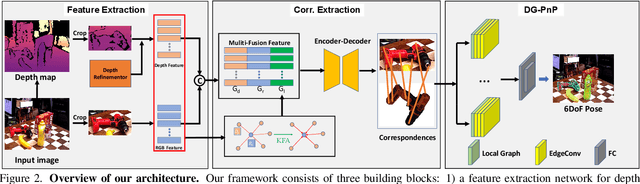
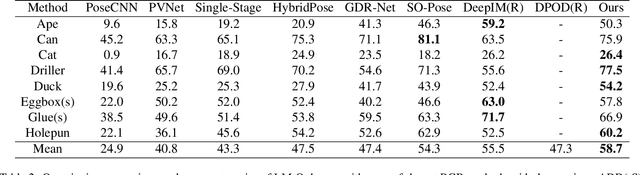
Monocular 6D pose estimation is a fundamental task in computer vision. Existing works often adopt a two-stage pipeline by establishing correspondences and utilizing a RANSAC algorithm to calculate 6 degrees-of-freedom (6DoF) pose. Recent works try to integrate differentiable RANSAC algorithms to achieve an end-to-end 6D pose estimation. However, most of them hardly consider the geometric features in 3D space, and ignore the topology cues when performing differentiable RANSAC algorithms. To this end, we proposed a Depth-Guided Edge Convolutional Network (DGECN) for 6D pose estimation task. We have made efforts from the following three aspects: 1) We take advantages ofestimated depth information to guide both the correspondences-extraction process and the cascaded differentiable RANSAC algorithm with geometric information. 2)We leverage the uncertainty ofthe estimated depth map to improve accuracy and robustness ofthe output 6D pose. 3) We propose a differentiable Perspective-n-Point(PnP) algorithm via edge convolution to explore the topology relations between 2D-3D correspondences. Experiments demonstrate that our proposed network outperforms current works on both effectiveness and efficiency.