Diffusion-Weighted Magnetic Resonance Brain Images Generation with Generative Adversarial Networks and Variational Autoencoders: A Comparison Study

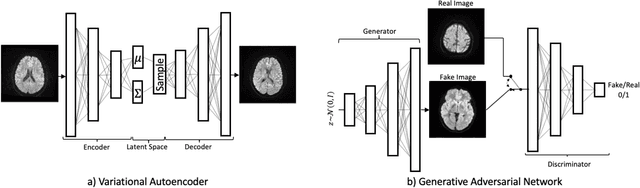
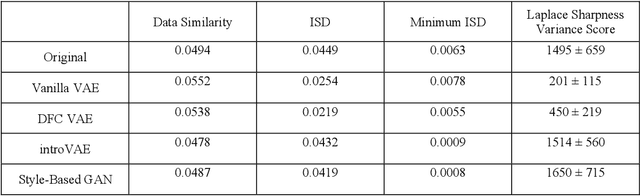
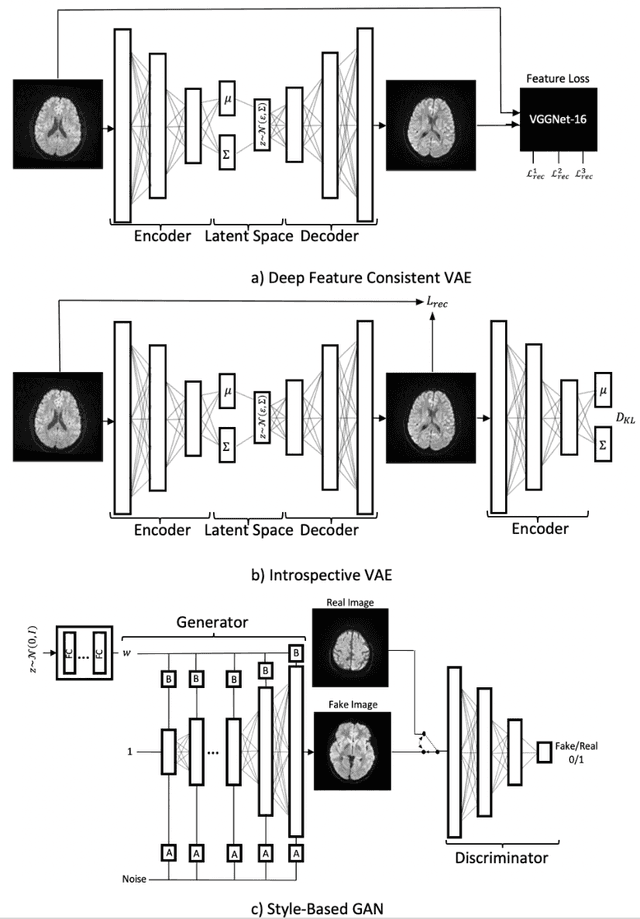
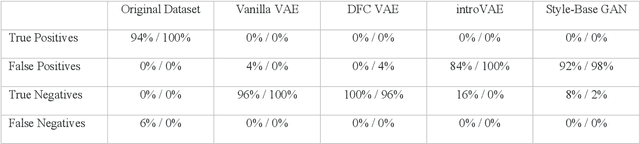
We show that high quality, diverse and realistic-looking diffusion-weighted magnetic resonance images can be synthesized using deep generative models. Based on professional neuroradiologists' evaluations and diverse metrics with respect to quality and diversity of the generated synthetic brain images, we present two networks, the Introspective Variational Autoencoder and the Style-Based GAN, that qualify for data augmentation in the medical field, where information is saved in a dispatched and inhomogeneous way and access to it is in many aspects restricted.

Factorised Representation Learning in Cardiac Image Analysis

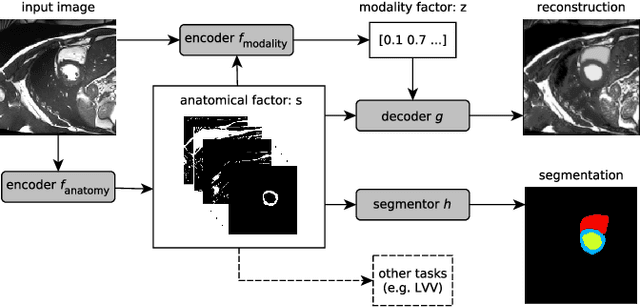
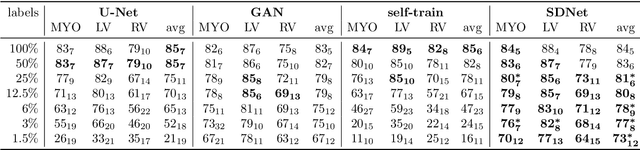
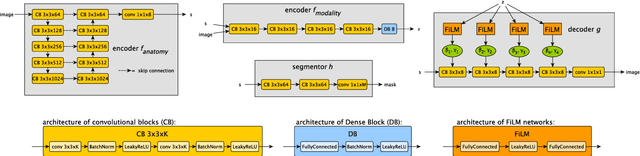
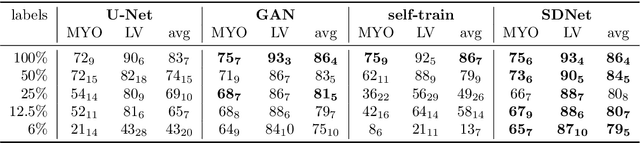
Typically, a medical image offers spatial information on the anatomy (and pathology) modulated by imaging specific characteristics. Many imaging modalities including Magnetic Resonance Imaging (MRI) and Computed Tomography (CT) can be interpreted in this way. We can venture further and consider that a medical image naturally factors into some spatial factors depicting anatomy and factors that denote the imaging characteristics. Here, we explicitly learn this decomposed (factorised) representation of imaging data, focusing in particular on cardiac images. We propose Spatial Decomposition Network (SDNet), which factorises 2D medical images into spatial anatomical factors and non-spatial imaging factors. We demonstrate that this high-level representation is ideally suited for several medical image analysis tasks, such as semi-supervised segmentation, multi-task segmentation and regression, and image-to-image synthesis. Specifically, we show that our model can match the performance of fully supervised segmentation models, using only a fraction of the labelled images. Critically, we show that our factorised representation also benefits from supervision obtained either when we use auxiliary tasks to train the model in a multi-task setting (e.g. regressing to known cardiac indices), or when aggregating multimodal data from different sources (e.g. pooling together MRI and CT data). To explore the properties of the learned factorisation, we perform latent-space arithmetic and show that we can synthesise CT from MR and vice versa, by swapping the modality factors. We also demonstrate that the factor holding image specific information can be used to predict the input modality with high accuracy.

Factorised spatial representation learning: application in semi-supervised myocardial segmentation

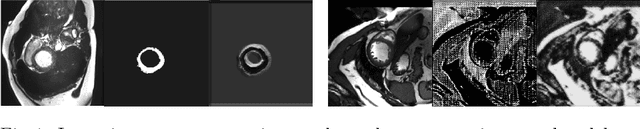
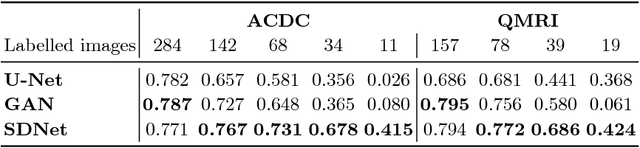
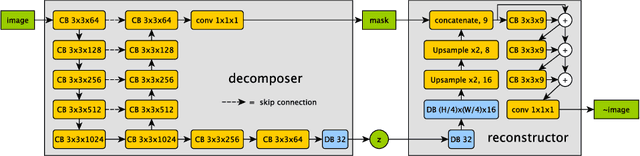
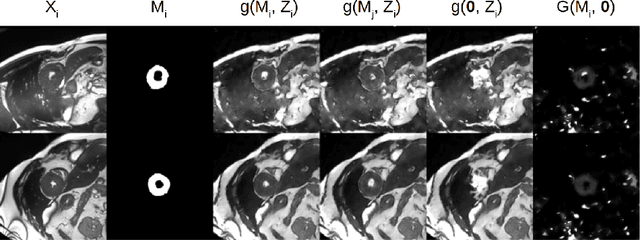
The success and generalisation of deep learning algorithms heavily depend on learning good feature representations. In medical imaging this entails representing anatomical information, as well as properties related to the specific imaging setting. Anatomical information is required to perform further analysis, whereas imaging information is key to disentangle scanner variability and potential artefacts. The ability to factorise these would allow for training algorithms only on the relevant information according to the task. To date, such factorisation has not been attempted. In this paper, we propose a methodology of latent space factorisation relying on the cycle-consistency principle. As an example application, we consider cardiac MR segmentation, where we separate information related to the myocardium from other features related to imaging and surrounding substructures. We demonstrate the proposed method's utility in a semi-supervised setting: we use very few labelled images together with many unlabelled images to train a myocardium segmentation neural network. Specifically, we achieve comparable performance to fully supervised networks using a fraction of labelled images in experiments on ACDC and a dataset from Edinburgh Imaging Facility QMRI. Code will be made available at https://github.com/agis85/spatial_factorisation.

Critical Parameters in Particle Swarm Optimisation

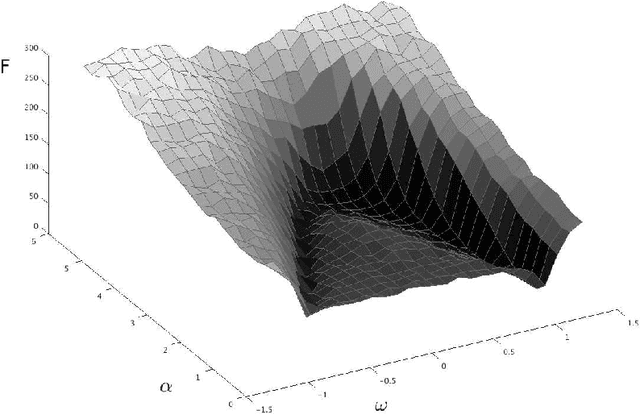
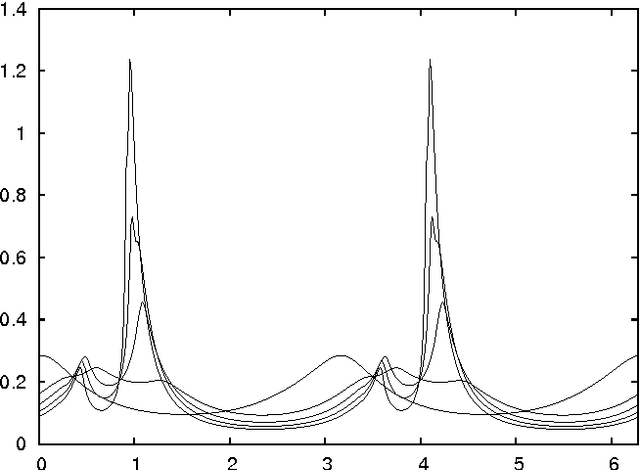
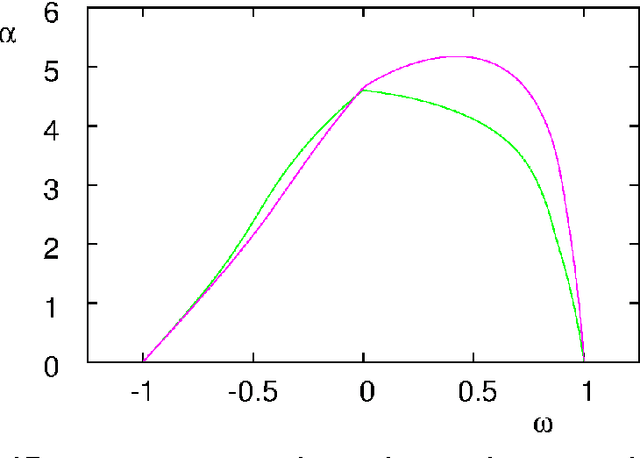
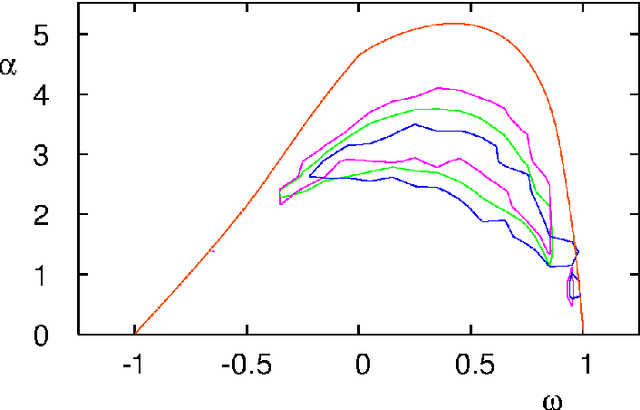
Particle swarm optimisation is a metaheuristic algorithm which finds reasonable solutions in a wide range of applied problems if suitable parameters are used. We study the properties of the algorithm in the framework of random dynamical systems which, due to the quasi-linear swarm dynamics, yields analytical results for the stability properties of the particles. Such considerations predict a relationship between the parameters of the algorithm that marks the edge between convergent and divergent behaviours. Comparison with simulations indicates that the algorithm performs best near this margin of instability.