Critical Parameters in Particle Swarm Optimisation

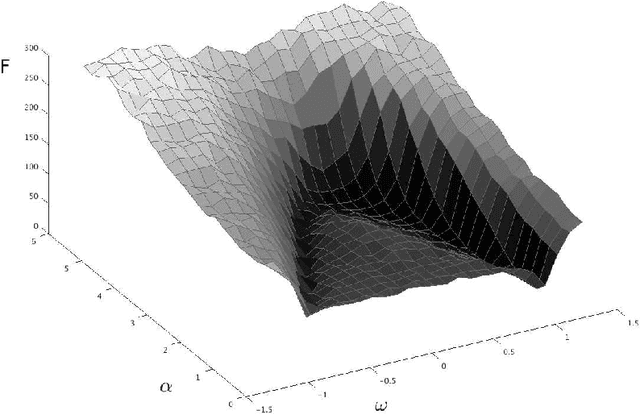
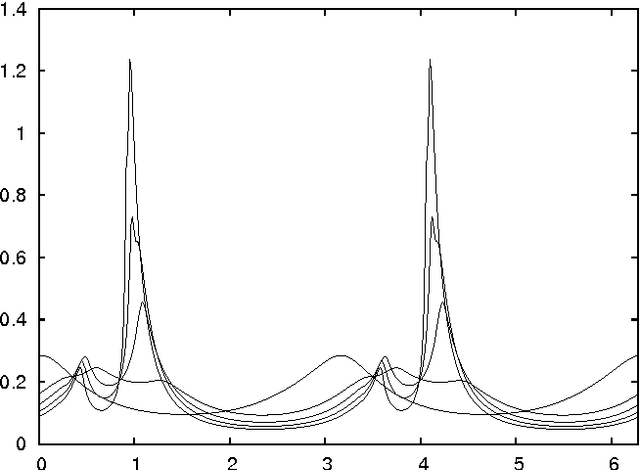
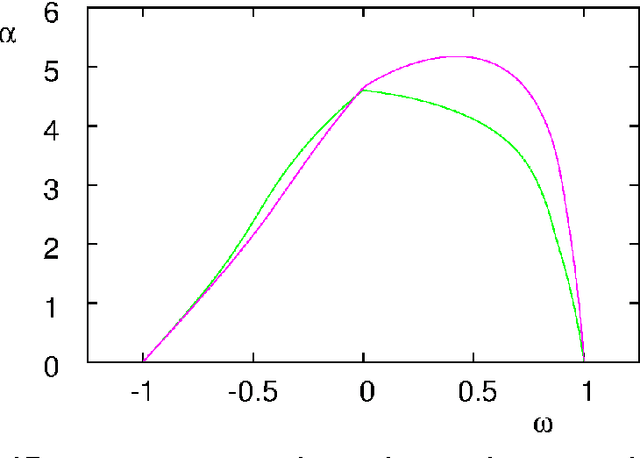
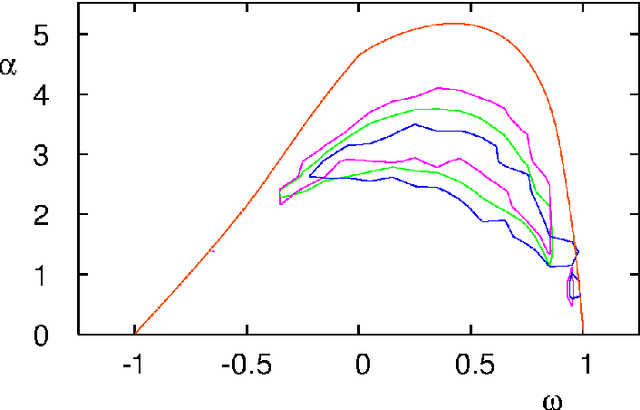
Particle swarm optimisation is a metaheuristic algorithm which finds reasonable solutions in a wide range of applied problems if suitable parameters are used. We study the properties of the algorithm in the framework of random dynamical systems which, due to the quasi-linear swarm dynamics, yields analytical results for the stability properties of the particles. Such considerations predict a relationship between the parameters of the algorithm that marks the edge between convergent and divergent behaviours. Comparison with simulations indicates that the algorithm performs best near this margin of instability.

CriPS: Critical Dynamics in Particle Swarm Optimization

Particle Swarm Optimisation (PSO) makes use of a dynamical system for solving a search task. Instead of adding search biases in order to improve performance in certain problems, we aim to remove algorithm-induced scales by controlling the swarm with a mechanism that is scale-free except possibly for a suppression of scales beyond the system size. In this way a very promising performance is achieved due to the balance of large-scale exploration and local search. The resulting algorithm shows evidence for self-organised criticality, brought about via the intrinsic dynamics of the swarm as it interacts with the objective function, rather than being explicitly specified. The Critical Particle Swarm (CriPS) can be easily combined with many existing extensions such as chaotic exploration, additional force terms or non-trivial topologies.