Critical Parameters in Particle Swarm Optimisation
Paper and Code
Nov 19, 2015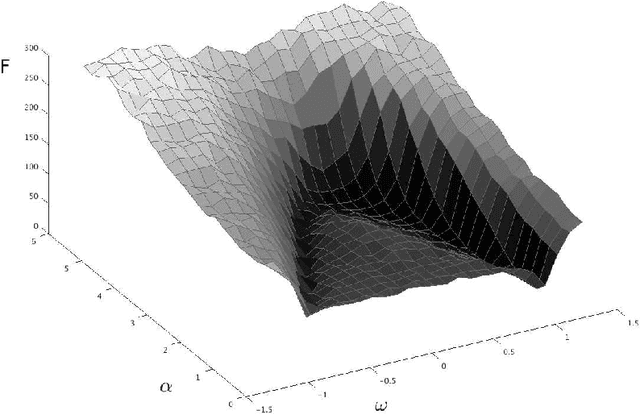
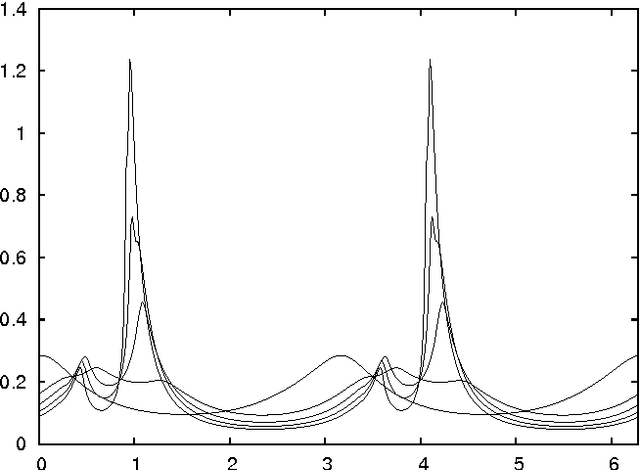
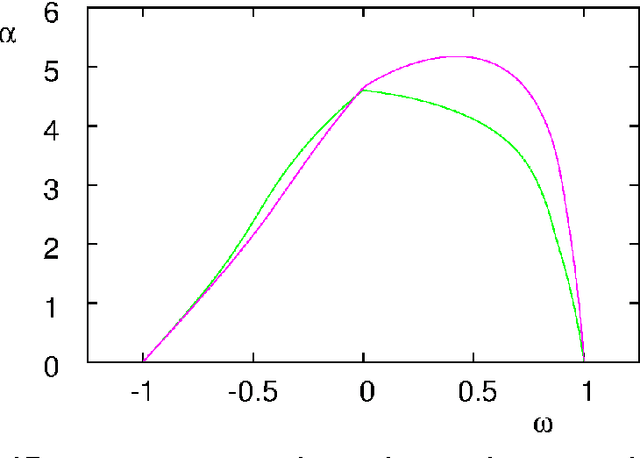
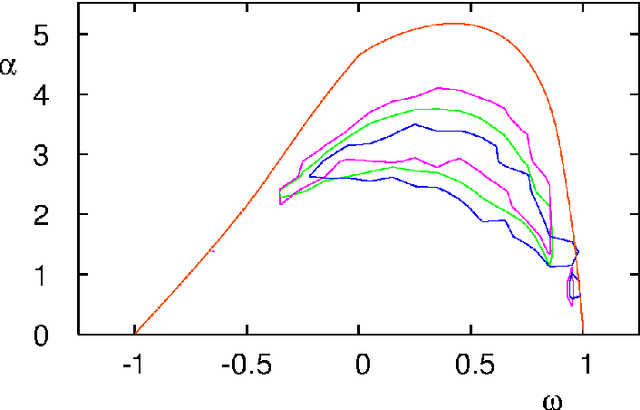
Particle swarm optimisation is a metaheuristic algorithm which finds reasonable solutions in a wide range of applied problems if suitable parameters are used. We study the properties of the algorithm in the framework of random dynamical systems which, due to the quasi-linear swarm dynamics, yields analytical results for the stability properties of the particles. Such considerations predict a relationship between the parameters of the algorithm that marks the edge between convergent and divergent behaviours. Comparison with simulations indicates that the algorithm performs best near this margin of instability.
* 9 pages, 5 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge