Marginalization Consistent Mixture of Separable Flows for Probabilistic Irregular Time Series Forecasting

Probabilistic forecasting models for joint distributions of targets in irregular time series are a heavily under-researched area in machine learning with, to the best of our knowledge, only three models researched so far: GPR, the Gaussian Process Regression model~\citep{Durichen2015.Multitask}, TACTiS, the Transformer-Attentional Copulas for Time Series~\cite{Drouin2022.Tactis, ashok2024tactis} and ProFITi \citep{Yalavarthi2024.Probabilistica}, a multivariate normalizing flow model based on invertible attention layers. While ProFITi, thanks to using multivariate normalizing flows, is the more expressive model with better predictive performance, we will show that it suffers from marginalization inconsistency: it does not guarantee that the marginal distributions of a subset of variables in its predictive distributions coincide with the directly predicted distributions of these variables. Also, TACTiS does not provide any guarantees for marginalization consistency. We develop a novel probabilistic irregular time series forecasting model, Marginalization Consistent Mixtures of Separable Flows (moses), that mixes several normalizing flows with (i) Gaussian Processes with full covariance matrix as source distributions and (ii) a separable invertible transformation, aiming to combine the expressivity of normalizing flows with the marginalization consistency of Gaussians. In experiments on four different datasets we show that moses outperforms other state-of-the-art marginalization consistent models, performs on par with ProFITi, but different from ProFITi, guarantee marginalization consistency.

Probabilistic Forecasting of Irregular Time Series via Conditional Flows

Probabilistic forecasting of irregularly sampled multivariate time series with missing values is an important problem in many fields, including health care, astronomy, and climate. State-of-the-art methods for the task estimate only marginal distributions of observations in single channels and at single timepoints, assuming a fixed-shape parametric distribution. In this work, we propose a novel model, ProFITi, for probabilistic forecasting of irregularly sampled time series with missing values using conditional normalizing flows. The model learns joint distributions over the future values of the time series conditioned on past observations and queried channels and times, without assuming any fixed shape of the underlying distribution. As model components, we introduce a novel invertible triangular attention layer and an invertible non-linear activation function on and onto the whole real line. We conduct extensive experiments on four datasets and demonstrate that the proposed model provides $4$ times higher likelihood over the previously best model.

Deep Learning for Fast Inference of Mechanistic Models' Parameters

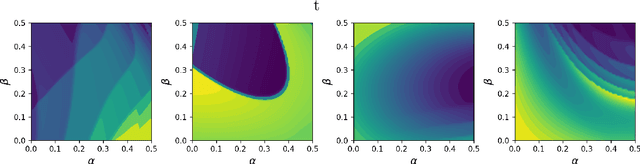
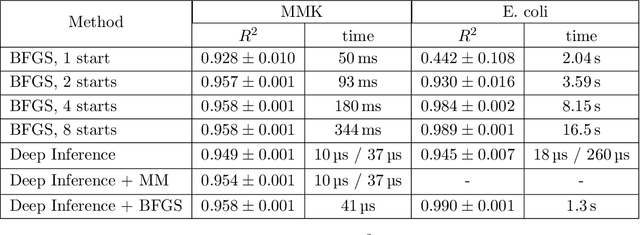
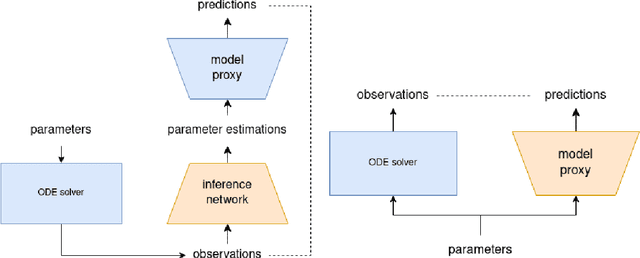
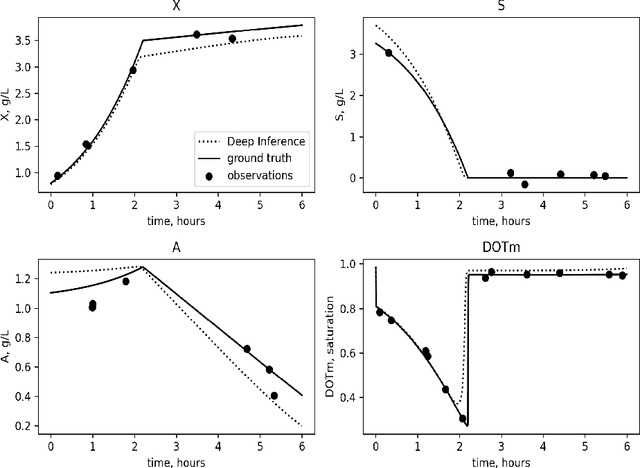
Inferring parameters of macro-kinetic growth models, typically represented by Ordinary Differential Equations (ODE), from the experimental data is a crucial step in bioprocess engineering. Conventionally, estimates of the parameters are obtained by fitting the mechanistic model to observations. Fitting, however, requires a significant computational power. Specifically, during the development of new bioprocesses that use previously unknown organisms or strains, efficient, robust, and computationally cheap methods for parameter estimation are of great value. In this work, we propose using Deep Neural Networks (NN) for directly predicting parameters of mechanistic models given observations. The approach requires spending computational resources for training a NN, nonetheless, once trained, such a network can provide parameter estimates orders of magnitude faster than conventional methods. We consider a training procedure that combines Neural Networks and mechanistic models. We demonstrate the performance of the proposed algorithms on data sampled from several mechanistic models used in bioengineering describing a typical industrial batch process and compare the proposed method, a typical gradient-based fitting procedure, and the combination of the two. We find that, while Neural Network estimates are slightly improved by further fitting, these estimates are measurably better than the fitting procedure alone.

Deep Set Neural Networks for forecasting asynchronous bioprocess timeseries

Cultivation experiments often produce sparse and irregular time series. Classical approaches based on mechanistic models, like Maximum Likelihood fitting or Monte-Carlo Markov chain sampling, can easily account for sparsity and time-grid irregularities, but most statistical and Machine Learning tools are not designed for handling sparse data out-of-the-box. Among popular approaches there are various schemes for filling missing values (imputation) and interpolation into a regular grid (alignment). However, such methods transfer the biases of the interpolation or imputation models to the target model. We show that Deep Set Neural Networks equipped with triplet encoding of the input data can successfully handle bio-process data without any need for imputation or alignment procedures. The method is agnostic to the particular nature of the time series and can be adapted for any task, for example, online monitoring, predictive control, design of experiments, etc. In this work, we focus on forecasting. We argue that such an approach is especially suitable for typical cultivation processes, demonstrate the performance of the method on several forecasting tasks using data generated from macrokinetic growth models under realistic conditions, and compare the method to a conventional fitting procedure and methods based on imputation and alignment.

Forecasting Irregularly Sampled Time Series using Graphs

Forecasting irregularly sampled time series with missing values is a crucial task for numerous real-world applications such as healthcare, astronomy, and climate sciences. State-of-the-art approaches to this problem rely on Ordinary Differential Equations (ODEs) but are known to be slow and to require additional features to handle missing values. To address this issue, we propose a novel model using Graphs for Forecasting Irregularly Sampled Time Series with missing values which we call GraFITi. GraFITi first converts the time series to a Sparsity Structure Graph which is a sparse bipartite graph, and then reformulates the forecasting problem as the edge weight prediction task in the graph. It uses the power of Graph Neural Networks to learn the graph and predict the target edge weights. We show that GraFITi can be used not only for our Sparsity Structure Graph but also for alternative graph representations of time series. GraFITi has been tested on 3 real-world and 1 synthetic irregularly sampled time series dataset with missing values and compared with various state-of-the-art models. The experimental results demonstrate that GraFITi improves the forecasting accuracy by up to 17% and reduces the run time up to 5 times compared to the state-of-the-art forecasting models.

Put Attention to Temporal Saliency Patterns of Multi-Horizon Time Series

Time series, sets of sequences in chronological order, are essential data in statistical research with many forecasting applications. Although recent performance in many Transformer-based models has been noticeable, long multi-horizon time series forecasting remains a very challenging task. Going beyond transformers in sequence translation and transduction research, we observe the effects of down-and-up samplings that can nudge temporal saliency patterns to emerge in time sequences. Motivated by the mentioned observation, in this paper, we propose a novel architecture, Temporal Saliency Detection (TSD), on top of the attention mechanism and apply it to multi-horizon time series prediction. We renovate the traditional encoder-decoder architecture by making as a series of deep convolutional blocks to work in tandem with the multi-head self-attention. The proposed TSD approach facilitates the multiresolution of saliency patterns upon condensed multi-heads, thus progressively enhancing complex time series forecasting. Experimental results illustrate that our proposed approach has significantly outperformed existing state-of-the-art methods across multiple standard benchmark datasets in many far-horizon forecasting settings. Overall, TSD achieves 31% and 46% relative improvement over the current state-of-the-art models in multivariate and univariate time series forecasting scenarios on standard benchmarks. The Git repository is available at https://github.com/duongtrung/time-series-temporal-saliency-patterns.

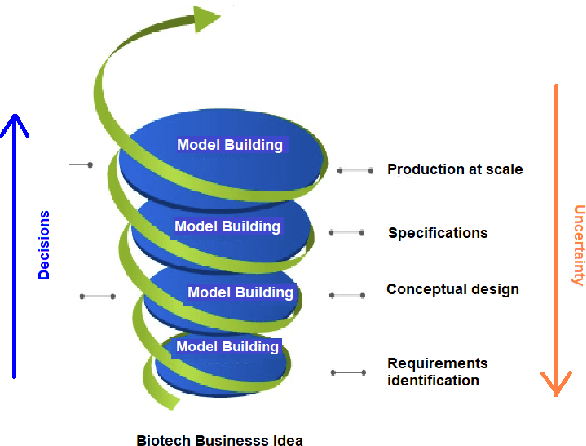
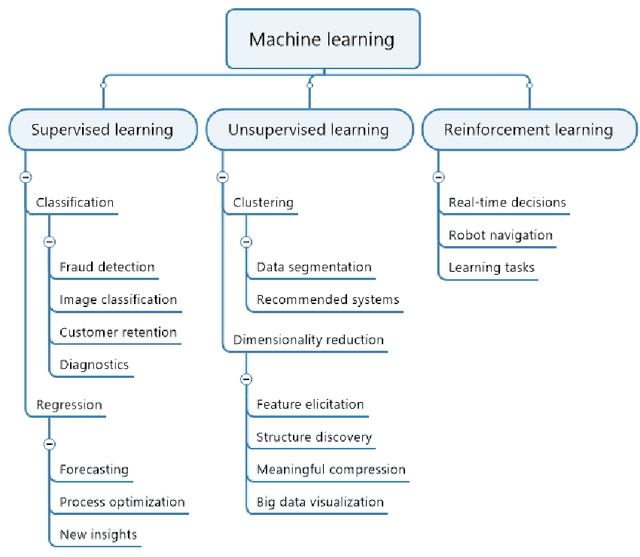
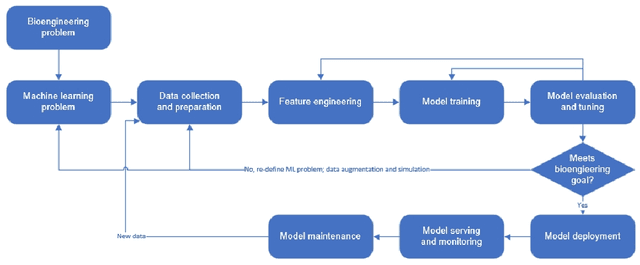
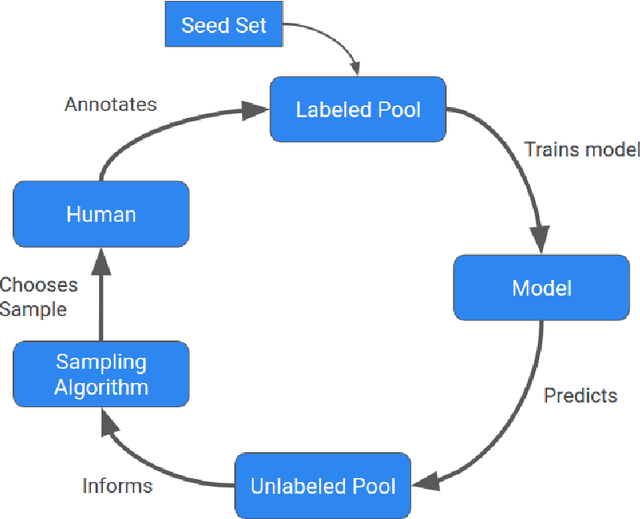
When Bioprocess Engineering Meets Machine Learning: A Survey from the Perspective of Automated Bioprocess Development

Machine learning (ML) has significantly contributed to the development of bioprocess engineering, but its application is still limited, hampering the enormous potential for bioprocess automation. ML for model building automation can be seen as a way of introducing another level of abstraction to focus expert humans in the most cognitive tasks of bioprocess development. First, probabilistic programming is used for the autonomous building of predictive models. Second, machine learning automatically assesses alternative decisions by planning experiments to test hypotheses and conducting investigations to gather informative data that focus on model selection based on the uncertainty of model predictions. This review provides a comprehensive overview of ML-based automation in bioprocess development. On the one hand, the biotech and bioengineering community should be aware of the potential and, most importantly, the limitation of existing ML solutions for their application in biotechnology and biopharma. On the other hand, it is essential to identify the missing links to enable the easy implementation of ML and Artificial Intelligence (AI) solutions in valuable solutions for the bio-community. We summarize recent ML implementation across several important subfields of bioprocess systems and raise two crucial challenges remaining the bottleneck of bioprocess automation and reducing uncertainty in biotechnology development. There is no one-fits-all procedure; however, this review should help identify the potential automation combining biotechnology and ML domains.

Yformer: U-Net Inspired Transformer Architecture for Far Horizon Time Series Forecasting

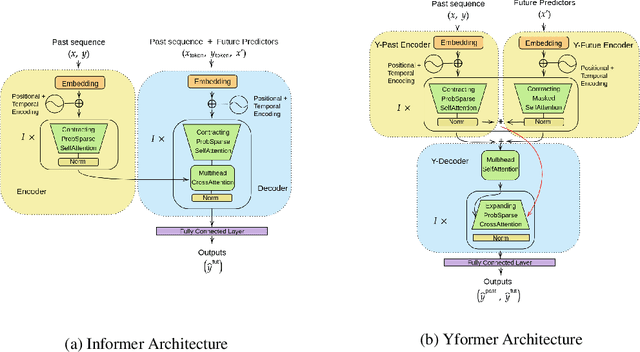
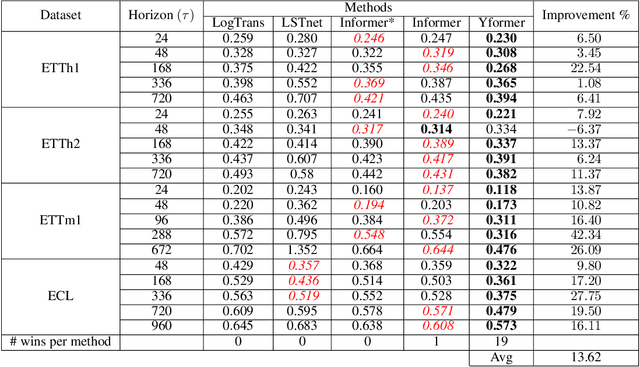
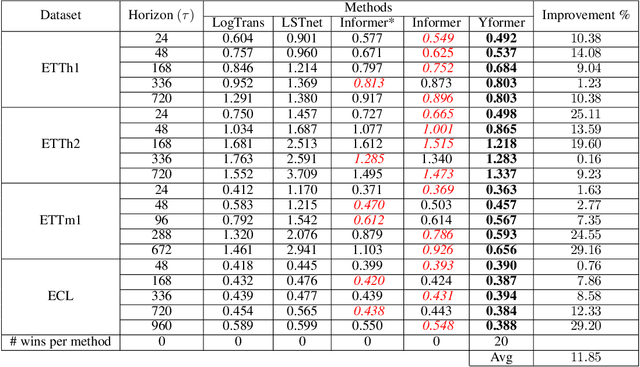
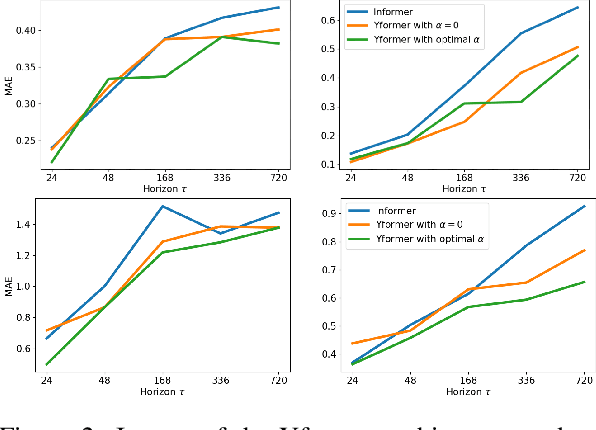
Time series data is ubiquitous in research as well as in a wide variety of industrial applications. Effectively analyzing the available historical data and providing insights into the far future allows us to make effective decisions. Recent research has witnessed the superior performance of transformer-based architectures, especially in the regime of far horizon time series forecasting. However, the current state of the art sparse Transformer architectures fail to couple down- and upsampling procedures to produce outputs in a similar resolution as the input. We propose the Yformer model, based on a novel Y-shaped encoder-decoder architecture that (1) uses direct connection from the downscaled encoder layer to the corresponding upsampled decoder layer in a U-Net inspired architecture, (2) Combines the downscaling/upsampling with sparse attention to capture long-range effects, and (3) stabilizes the encoder-decoder stacks with the addition of an auxiliary reconstruction loss. Extensive experiments have been conducted with relevant baselines on four benchmark datasets, demonstrating an average improvement of 19.82, 18.41 percentage MSE and 13.62, 11.85 percentage MAE in comparison to the current state of the art for the univariate and the multivariate settings respectively.