TabResFlow: A Normalizing Spline Flow Model for Probabilistic Univariate Tabular Regression

Tabular regression is a well-studied problem with numerous industrial applications, yet most existing approaches focus on point estimation, often leading to overconfident predictions. This issue is particularly critical in industrial automation, where trustworthy decision-making is essential. Probabilistic regression models address this challenge by modeling prediction uncertainty. However, many conventional methods assume a fixed-shape distribution (typically Gaussian), and resort to estimating distribution parameters. This assumption is often restrictive, as real-world target distributions can be highly complex. To overcome this limitation, we introduce TabResFlow, a Normalizing Spline Flow model designed specifically for univariate tabular regression, where commonly used simple flow networks like RealNVP and Masked Autoregressive Flow (MAF) are unsuitable. TabResFlow consists of three key components: (1) An MLP encoder for each numerical feature. (2) A fully connected ResNet backbone for expressive feature extraction. (3) A conditional spline-based normalizing flow for flexible and tractable density estimation. We evaluate TabResFlow on nine public benchmark datasets, demonstrating that it consistently surpasses existing probabilistic regression models on likelihood scores. Our results demonstrate 9.64% improvement compared to the strongest probabilistic regression model (TreeFlow), and on average 5.6 times speed-up in inference time compared to the strongest deep learning alternative (NodeFlow). Additionally, we validate the practical applicability of TabResFlow in a real-world used car price prediction task under selective regression. To measure performance in this setting, we introduce a novel Area Under Risk Coverage (AURC) metric and show that TabResFlow achieves superior results across this metric.

The Role of Active Learning in Modern Machine Learning

Even though Active Learning (AL) is widely studied, it is rarely applied in contexts outside its own scientific literature. We posit that the reason for this is AL's high computational cost coupled with the comparatively small lifts it is typically able to generate in scenarios with few labeled points. In this work we study the impact of different methods to combat this low data scenario, namely data augmentation (DA), semi-supervised learning (SSL) and AL. We find that AL is by far the least efficient method of solving the low data problem, generating a lift of only 1-4\% over random sampling, while DA and SSL methods can generate up to 60\% lift in combination with random sampling. However, when AL is combined with strong DA and SSL techniques, it surprisingly is still able to provide improvements. Based on these results, we frame AL not as a method to combat missing labels, but as the final building block to squeeze the last bits of performance out of data after appropriate DA and SSL methods as been applied.

Physiome-ODE: A Benchmark for Irregularly Sampled Multivariate Time Series Forecasting Based on Biological ODEs

State-of-the-art methods for forecasting irregularly sampled time series with missing values predominantly rely on just four datasets and a few small toy examples for evaluation. While ordinary differential equations (ODE) are the prevalent models in science and engineering, a baseline model that forecasts a constant value outperforms ODE-based models from the last five years on three of these existing datasets. This unintuitive finding hampers further research on ODE-based models, a more plausible model family. In this paper, we develop a methodology to generate irregularly sampled multivariate time series (IMTS) datasets from ordinary differential equations and to select challenging instances via rejection sampling. Using this methodology, we create Physiome-ODE, a large and sophisticated benchmark of IMTS datasets consisting of 50 individual datasets, derived from real-world ordinary differential equations from research in biology. Physiome-ODE is the first benchmark for IMTS forecasting that we are aware of and an order of magnitude larger than the current evaluation setting of four datasets. Using our benchmark Physiome-ODE, we show qualitatively completely different results than those derived from the current four datasets: on Physiome-ODE ODE-based models can play to their strength and our benchmark can differentiate in a meaningful way between different IMTS forecasting models. This way, we expect to give a new impulse to research on ODE-based time series modeling.

Marginalization Consistent Mixture of Separable Flows for Probabilistic Irregular Time Series Forecasting

Probabilistic forecasting models for joint distributions of targets in irregular time series are a heavily under-researched area in machine learning with, to the best of our knowledge, only three models researched so far: GPR, the Gaussian Process Regression model~\citep{Durichen2015.Multitask}, TACTiS, the Transformer-Attentional Copulas for Time Series~\cite{Drouin2022.Tactis, ashok2024tactis} and ProFITi \citep{Yalavarthi2024.Probabilistica}, a multivariate normalizing flow model based on invertible attention layers. While ProFITi, thanks to using multivariate normalizing flows, is the more expressive model with better predictive performance, we will show that it suffers from marginalization inconsistency: it does not guarantee that the marginal distributions of a subset of variables in its predictive distributions coincide with the directly predicted distributions of these variables. Also, TACTiS does not provide any guarantees for marginalization consistency. We develop a novel probabilistic irregular time series forecasting model, Marginalization Consistent Mixtures of Separable Flows (moses), that mixes several normalizing flows with (i) Gaussian Processes with full covariance matrix as source distributions and (ii) a separable invertible transformation, aiming to combine the expressivity of normalizing flows with the marginalization consistency of Gaussians. In experiments on four different datasets we show that moses outperforms other state-of-the-art marginalization consistent models, performs on par with ProFITi, but different from ProFITi, guarantee marginalization consistency.

Functional Latent Dynamics for Irregularly Sampled Time Series Forecasting

Irregularly sampled time series with missing values are often observed in multiple real-world applications such as healthcare, climate and astronomy. They pose a significant challenge to standard deep learn- ing models that operate only on fully observed and regularly sampled time series. In order to capture the continuous dynamics of the irreg- ular time series, many models rely on solving an Ordinary Differential Equation (ODE) in the hidden state. These ODE-based models tend to perform slow and require large memory due to sequential operations and a complex ODE solver. As an alternative to complex ODE-based mod- els, we propose a family of models called Functional Latent Dynamics (FLD). Instead of solving the ODE, we use simple curves which exist at all time points to specify the continuous latent state in the model. The coefficients of these curves are learned only from the observed values in the time series ignoring the missing values. Through extensive experi- ments, we demonstrate that FLD achieves better performance compared to the best ODE-based model while reducing the runtime and memory overhead. Specifically, FLD requires an order of magnitude less time to infer the forecasts compared to the best performing forecasting model.

Are EEG Sequences Time Series? EEG Classification with Time Series Models and Joint Subject Training

As with most other data domains, EEG data analysis relies on rich domain-specific preprocessing. Beyond such preprocessing, machine learners would hope to deal with such data as with any other time series data. For EEG classification many models have been developed with layer types and architectures we typically do not see in time series classification. Furthermore, typically separate models for each individual subject are learned, not one model for all of them. In this paper, we systematically study the differences between EEG classification models and generic time series classification models. We describe three different model setups to deal with EEG data from different subjects, subject-specific models (most EEG literature), subject-agnostic models and subject-conditional models. In experiments on three datasets, we demonstrate that off-the-shelf time series classification models trained per subject perform close to EEG classification models, but that do not quite reach the performance of domain-specific modeling. Additionally, we combine time-series models with subject embeddings to train one joint subject-conditional classifier on all subjects. The resulting models are competitive with dedicated EEG models in 2 out of 3 datasets, even outperforming all EEG methods on one of them.

Probabilistic Forecasting of Irregular Time Series via Conditional Flows

Probabilistic forecasting of irregularly sampled multivariate time series with missing values is an important problem in many fields, including health care, astronomy, and climate. State-of-the-art methods for the task estimate only marginal distributions of observations in single channels and at single timepoints, assuming a fixed-shape parametric distribution. In this work, we propose a novel model, ProFITi, for probabilistic forecasting of irregularly sampled time series with missing values using conditional normalizing flows. The model learns joint distributions over the future values of the time series conditioned on past observations and queried channels and times, without assuming any fixed shape of the underlying distribution. As model components, we introduce a novel invertible triangular attention layer and an invertible non-linear activation function on and onto the whole real line. We conduct extensive experiments on four datasets and demonstrate that the proposed model provides $4$ times higher likelihood over the previously best model.

Forecasting Early with Meta Learning

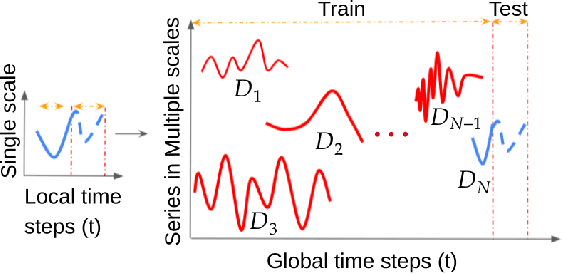
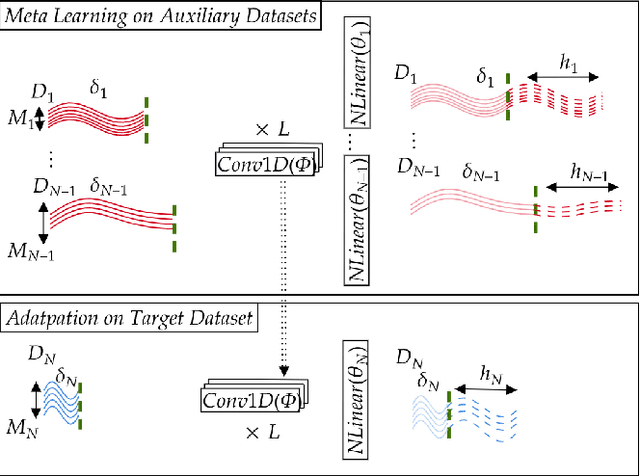
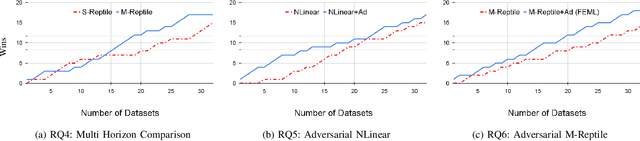
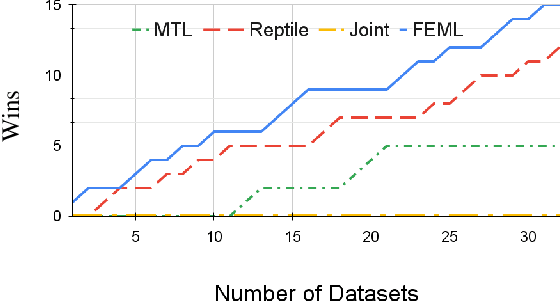
In the early observation period of a time series, there might be only a few historic observations available to learn a model. However, in cases where an existing prior set of datasets is available, Meta learning methods can be applicable. In this paper, we devise a Meta learning method that exploits samples from additional datasets and learns to augment time series through adversarial learning as an auxiliary task for the target dataset. Our model (FEML), is equipped with a shared Convolutional backbone that learns features for varying length inputs from different datasets and has dataset specific heads to forecast for different output lengths. We show that FEML can meta learn across datasets and by additionally learning on adversarial generated samples as auxiliary samples for the target dataset, it can improve the forecasting performance compared to single task learning, and various solutions adapted from Joint learning, Multi-task learning and classic forecasting baselines.

Forecasting Irregularly Sampled Time Series using Graphs

Forecasting irregularly sampled time series with missing values is a crucial task for numerous real-world applications such as healthcare, astronomy, and climate sciences. State-of-the-art approaches to this problem rely on Ordinary Differential Equations (ODEs) but are known to be slow and to require additional features to handle missing values. To address this issue, we propose a novel model using Graphs for Forecasting Irregularly Sampled Time Series with missing values which we call GraFITi. GraFITi first converts the time series to a Sparsity Structure Graph which is a sparse bipartite graph, and then reformulates the forecasting problem as the edge weight prediction task in the graph. It uses the power of Graph Neural Networks to learn the graph and predict the target edge weights. We show that GraFITi can be used not only for our Sparsity Structure Graph but also for alternative graph representations of time series. GraFITi has been tested on 3 real-world and 1 synthetic irregularly sampled time series dataset with missing values and compared with various state-of-the-art models. The experimental results demonstrate that GraFITi improves the forecasting accuracy by up to 17% and reduces the run time up to 5 times compared to the state-of-the-art forecasting models.

Tripletformer for Probabilistic Interpolation of Asynchronous Time Series

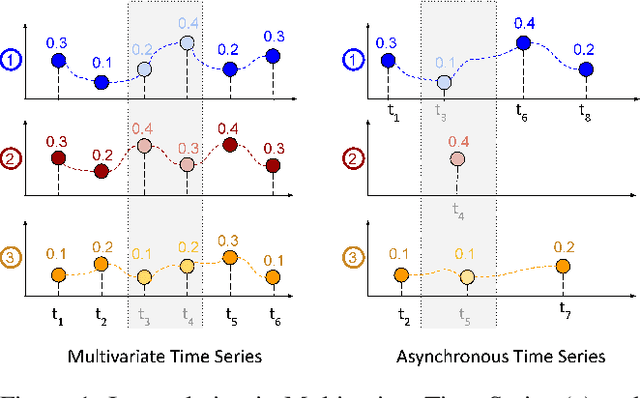
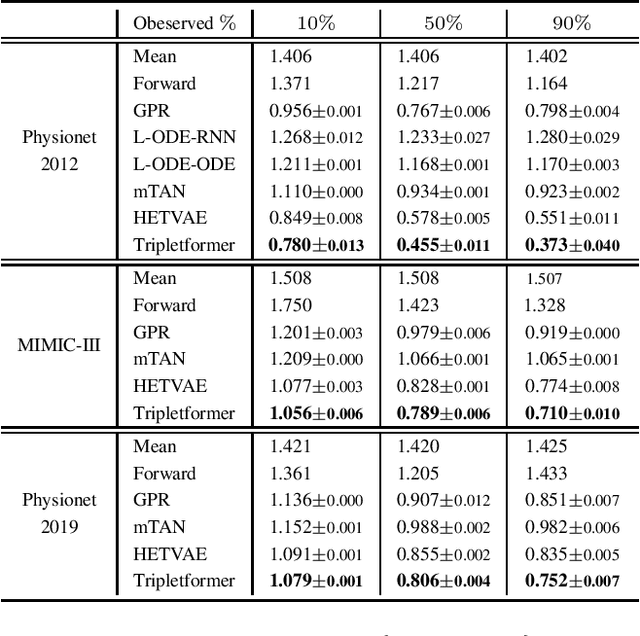
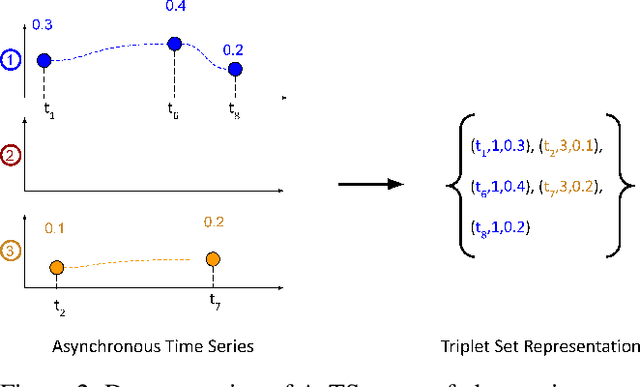
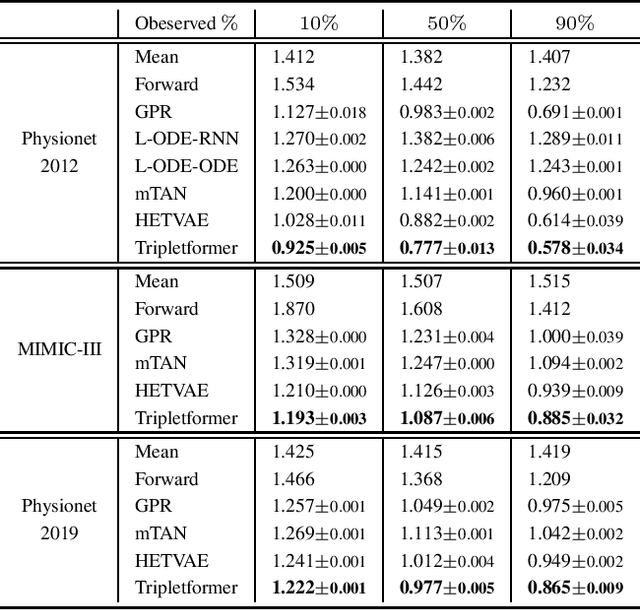
Asynchronous time series are often observed in several applications such as health care, astronomy, and climate science, and pose a significant challenge to the standard deep learning architectures. Interpolation of asynchronous time series is vital for many real-world tasks like root cause analysis, and medical diagnosis. In this paper, we propose a novel encoder-decoder architecture called Tripletformer, which works on the set of observations where each set element is a triple of time, channel, and value, for the probabilistic interpolation of the asynchronous time series. Both the encoder and the decoder of the Tripletformer are modeled using attention layers and fully connected layers and are invariant to the order in which set elements are presented. The proposed Tripletformer is compared with a range of baselines over multiple real-world and synthetic asynchronous time series datasets, and the experimental results attest that it produces more accurate and certain interpolations. We observe an improvement in negative loglikelihood error up to 33% over real and 800% over synthetic asynchronous time series datasets compared to the state-of-the-art model using the Tripletformer.