A Semidefinite Relaxation Approach for Fair Graph Clustering

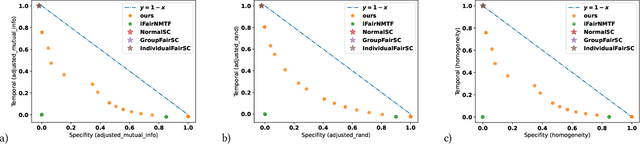
Fair graph clustering is crucial for ensuring equitable representation and treatment of diverse communities in network analysis. Traditional methods often ignore disparities among social, economic, and demographic groups, perpetuating biased outcomes and reinforcing inequalities. This study introduces fair graph clustering within the framework of the disparate impact doctrine, treating it as a joint optimization problem integrating clustering quality and fairness constraints. Given the NP-hard nature of this problem, we employ a semidefinite relaxation approach to approximate the underlying optimization problem. For up to medium-sized graphs, we utilize a singular value decomposition-based algorithm, while for larger graphs, we propose a novel algorithm based on the alternative direction method of multipliers. Unlike existing methods, our formulation allows for tuning the trade-off between clustering quality and fairness. Experimental results on graphs generated from the standard stochastic block model demonstrate the superiority of our approach in achieving an optimal accuracy-fairness trade-off compared to state-of-the-art methods.

f-FERM: A Scalable Framework for Robust Fair Empirical Risk Minimization

Training and deploying machine learning models that meet fairness criteria for protected groups are fundamental in modern artificial intelligence. While numerous constraints and regularization terms have been proposed in the literature to promote fairness in machine learning tasks, most of these methods are not amenable to stochastic optimization due to the complex and nonlinear structure of constraints and regularizers. Here, the term "stochastic" refers to the ability of the algorithm to work with small mini-batches of data. Motivated by the limitation of existing literature, this paper presents a unified stochastic optimization framework for fair empirical risk minimization based on f-divergence measures (f-FERM). The proposed stochastic algorithm enjoys theoretical convergence guarantees. In addition, our experiments demonstrate the superiority of fairness-accuracy tradeoffs offered by f-FERM for almost all batch sizes (ranging from full-batch to batch size of one). Moreover, we show that our framework can be extended to the case where there is a distribution shift from training to the test data. Our extension is based on a distributionally robust optimization reformulation of f-FERM objective under $L_p$ norms as uncertainty sets. Again, in this distributionally robust setting, f-FERM not only enjoys theoretical convergence guarantees but also outperforms other baselines in the literature in the tasks involving distribution shifts. An efficient stochastic implementation of $f$-FERM is publicly available.

Dr. FERMI: A Stochastic Distributionally Robust Fair Empirical Risk Minimization Framework

While training fair machine learning models has been studied extensively in recent years, most developed methods rely on the assumption that the training and test data have similar distributions. In the presence of distribution shifts, fair models may behave unfairly on test data. There have been some developments for fair learning robust to distribution shifts to address this shortcoming. However, most proposed solutions are based on the assumption of having access to the causal graph describing the interaction of different features. Moreover, existing algorithms require full access to data and cannot be used when small batches are used (stochastic/batch implementation). This paper proposes the first stochastic distributionally robust fairness framework with convergence guarantees that do not require knowledge of the causal graph. More specifically, we formulate the fair inference in the presence of the distribution shift as a distributionally robust optimization problem under $L_p$ norm uncertainty sets with respect to the Exponential Renyi Mutual Information (ERMI) as the measure of fairness violation. We then discuss how the proposed method can be implemented in a stochastic fashion. We have evaluated the presented framework's performance and efficiency through extensive experiments on real datasets consisting of distribution shifts.

Improving Adversarial Robustness via Joint Classification and Multiple Explicit Detection Classes

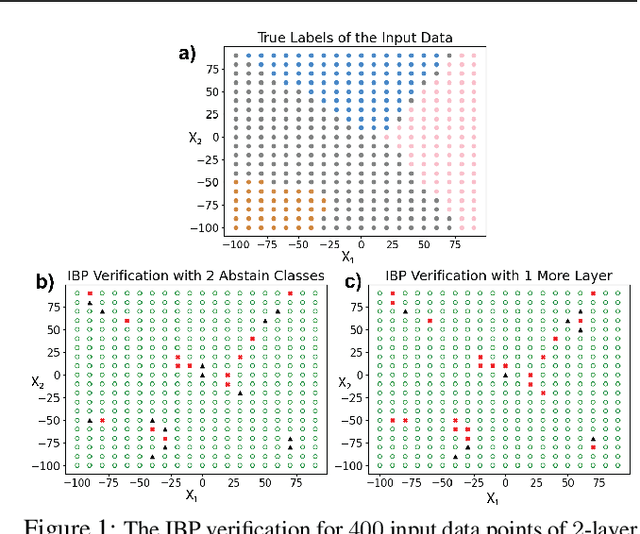
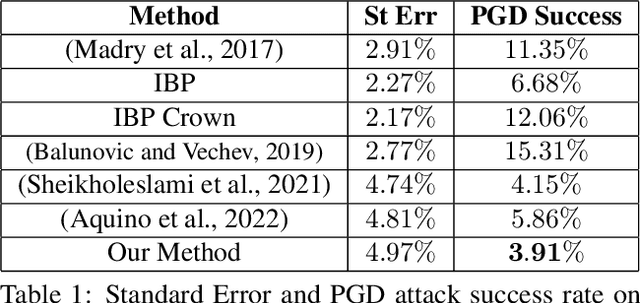
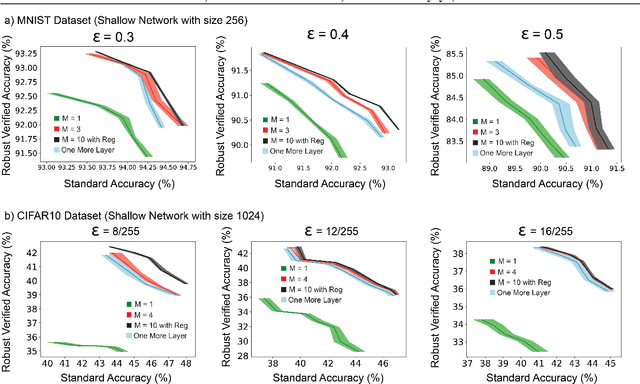
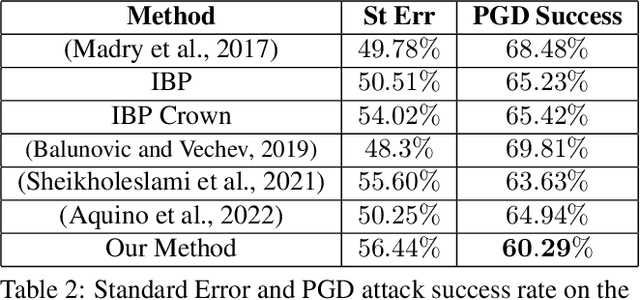
This work concerns the development of deep networks that are certifiably robust to adversarial attacks. Joint robust classification-detection was recently introduced as a certified defense mechanism, where adversarial examples are either correctly classified or assigned to the "abstain" class. In this work, we show that such a provable framework can benefit by extension to networks with multiple explicit abstain classes, where the adversarial examples are adaptively assigned to those. We show that naively adding multiple abstain classes can lead to "model degeneracy", then we propose a regularization approach and a training method to counter this degeneracy by promoting full use of the multiple abstain classes. Our experiments demonstrate that the proposed approach consistently achieves favorable standard vs. robust verified accuracy tradeoffs, outperforming state-of-the-art algorithms for various choices of number of abstain classes.

RIFLE: Robust Inference from Low Order Marginals

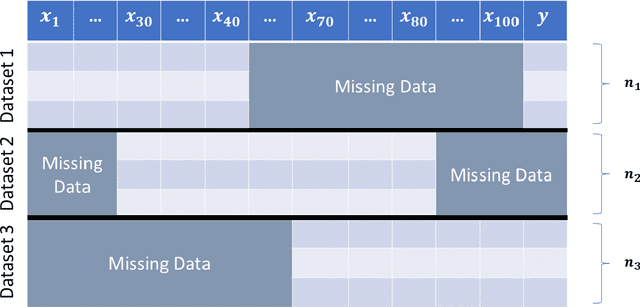
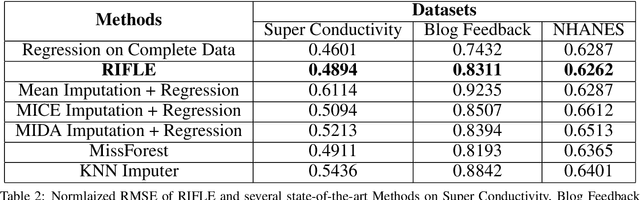
The ubiquity of missing values in real-world datasets poses a challenge for statistical inference and can prevent similar datasets from being analyzed in the same study, precluding many existing datasets from being used for new analyses. While an extensive collection of packages and algorithms have been developed for data imputation, the overwhelming majority perform poorly if there are many missing values and low sample size, which are unfortunately common characteristics in empirical data. Such low-accuracy estimations adversely affect the performance of downstream statistical models. We develop a statistical inference framework for predicting the target variable without imputing missing values. Our framework, RIFLE (Robust InFerence via Low-order moment Estimations), estimates low-order moments with corresponding confidence intervals to learn a distributionally robust model. We specialize our framework to linear regression and normal discriminant analysis, and we provide convergence and performance guarantees. This framework can also be adapted to impute missing data. In numerical experiments, we compare RIFLE with state-of-the-art approaches (including MICE, Amelia, MissForest, KNN-imputer, MIDA, and Mean Imputer). Our experiments demonstrate that RIFLE outperforms other benchmark algorithms when the percentage of missing values is high and/or when the number of data points is relatively small. RIFLE is publicly available.

FERMI: Fair Empirical Risk Minimization via Exponential Rényi Mutual Information

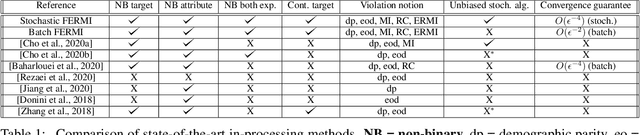
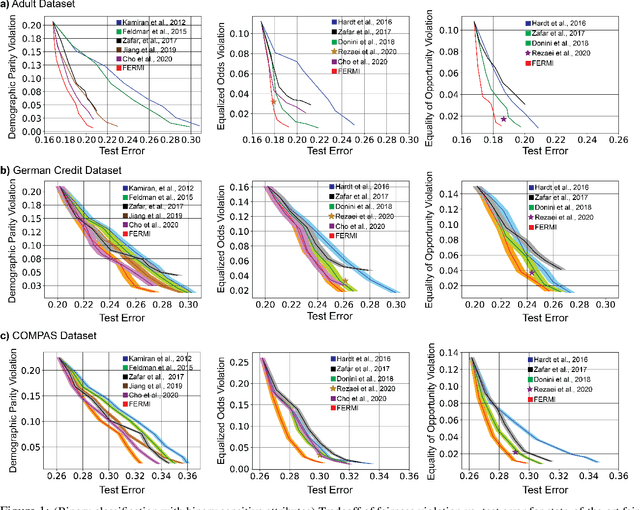
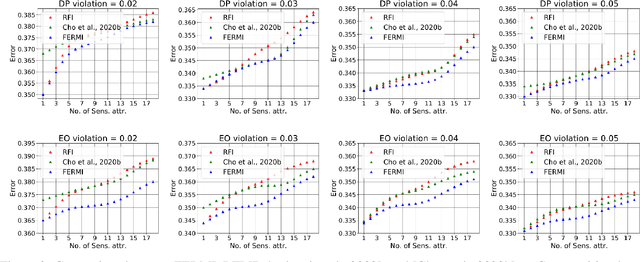
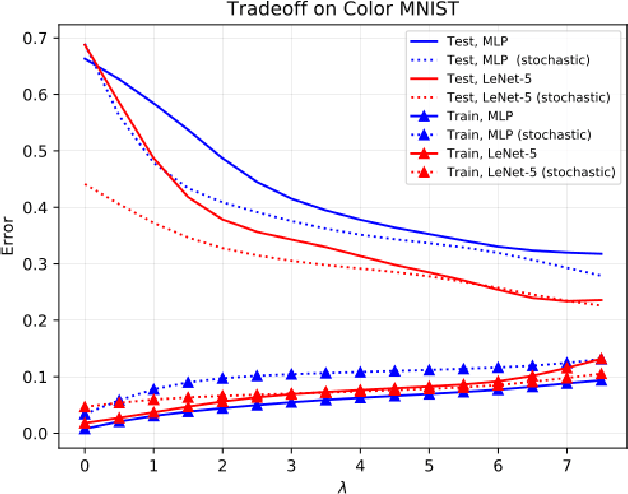
In this paper, we propose a new notion of fairness violation, called Exponential R\'enyi Mutual Information (ERMI). We show that ERMI is a strong fairness violation notion in the sense that it provides upper bound guarantees on existing notions of fairness violation. We then propose the Fair Empirical Risk Minimization via ERMI regularization framework, called FERMI. Whereas most existing in-processing fairness algorithms are deterministic, we provide the first stochastic optimization method with a provable convergence guarantee for solving FERMI. Our stochastic algorithm is amenable to large-scale problems, as we demonstrate experimentally. In addition, we provide a batch (deterministic) algorithm for solving FERMI with the optimal rate of convergence. Both of our algorithms are applicable to problems with multiple (non-binary) sensitive attributes and non-binary targets. Extensive experiments show that FERMI achieves the most favorable tradeoffs between fairness violation and test accuracy across various problem setups compared with state-of-the-art baselines.

When Does Non-Orthogonal Tensor Decomposition Have No Spurious Local Minima?

We study the optimization problem for decomposing $d$ dimensional fourth-order Tensors with $k$ non-orthogonal components. We derive \textit{deterministic} conditions under which such a problem does not have spurious local minima. In particular, we show that if $\kappa = \frac{\lambda_{max}}{\lambda_{min}} < \frac{5}{4}$, and incoherence coefficient is of the order $O(\frac{1}{\sqrt{d}})$, then all the local minima are globally optimal. Using standard techniques, these conditions could be easily transformed into conditions that would hold with high probability in high dimensions when the components are generated randomly. Finally, we prove that the tensor power method with deflation and restarts could efficiently extract all the components within a tolerance level $O(\kappa \sqrt{k\tau^3})$ that seems to be the noise floor of non-orthogonal tensor decomposition.

Rényi Fair Inference

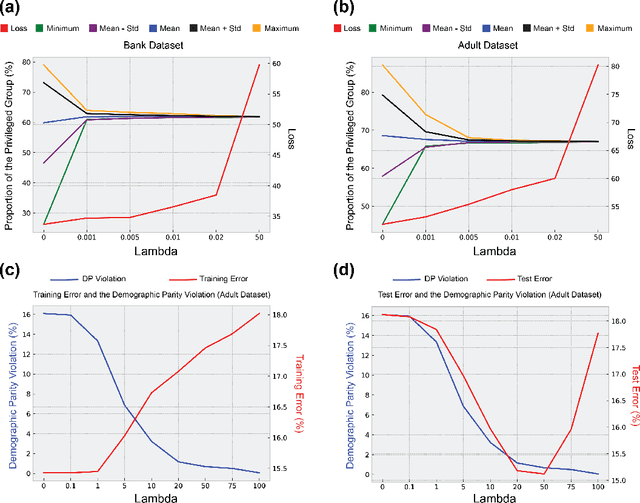
Machine learning algorithms have been increasingly deployed in critical automated decision-making systems that directly affect human lives. When these algorithms are only trained to minimize the training/test error, they could suffer from systematic discrimination against individuals based on their sensitive attributes such as gender or race. Recently, there has been a surge in machine learning society to develop algorithms for fair machine learning. In particular, many adversarial learning procedures have been proposed to impose fairness. Unfortunately, these algorithms either can only impose fairness up to first-order dependence between the variables, or they lack computational convergence guarantees. In this paper, we use R\'enyi correlation as a measure of fairness of machine learning models and develop a general training framework to impose fairness. In particular, we propose a min-max formulation which balances the accuracy and fairness when solved to optimality. For the case of discrete sensitive attributes, we suggest an iterative algorithm with theoretical convergence guarantee for solving the proposed min-max problem. Our algorithm and analysis are then specialized to fair classification and the fair clustering problem under disparate impact doctrine. Finally, the performance of the proposed R\'enyi fair inference framework is evaluated on Adult and Bank datasets.