A Semidefinite Relaxation Approach for Fair Graph Clustering
Paper and Code
Oct 19, 2024
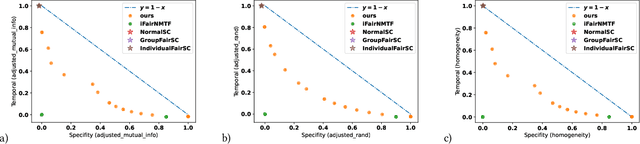


Fair graph clustering is crucial for ensuring equitable representation and treatment of diverse communities in network analysis. Traditional methods often ignore disparities among social, economic, and demographic groups, perpetuating biased outcomes and reinforcing inequalities. This study introduces fair graph clustering within the framework of the disparate impact doctrine, treating it as a joint optimization problem integrating clustering quality and fairness constraints. Given the NP-hard nature of this problem, we employ a semidefinite relaxation approach to approximate the underlying optimization problem. For up to medium-sized graphs, we utilize a singular value decomposition-based algorithm, while for larger graphs, we propose a novel algorithm based on the alternative direction method of multipliers. Unlike existing methods, our formulation allows for tuning the trade-off between clustering quality and fairness. Experimental results on graphs generated from the standard stochastic block model demonstrate the superiority of our approach in achieving an optimal accuracy-fairness trade-off compared to state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge