RIFLE: Robust Inference from Low Order Marginals

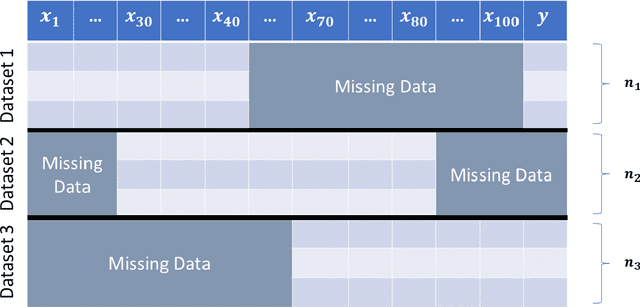
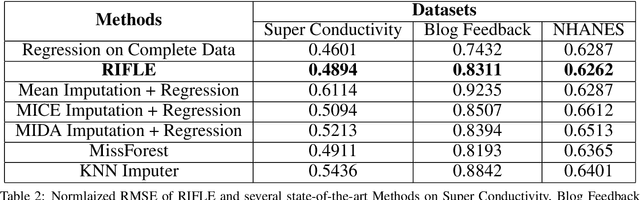
The ubiquity of missing values in real-world datasets poses a challenge for statistical inference and can prevent similar datasets from being analyzed in the same study, precluding many existing datasets from being used for new analyses. While an extensive collection of packages and algorithms have been developed for data imputation, the overwhelming majority perform poorly if there are many missing values and low sample size, which are unfortunately common characteristics in empirical data. Such low-accuracy estimations adversely affect the performance of downstream statistical models. We develop a statistical inference framework for predicting the target variable without imputing missing values. Our framework, RIFLE (Robust InFerence via Low-order moment Estimations), estimates low-order moments with corresponding confidence intervals to learn a distributionally robust model. We specialize our framework to linear regression and normal discriminant analysis, and we provide convergence and performance guarantees. This framework can also be adapted to impute missing data. In numerical experiments, we compare RIFLE with state-of-the-art approaches (including MICE, Amelia, MissForest, KNN-imputer, MIDA, and Mean Imputer). Our experiments demonstrate that RIFLE outperforms other benchmark algorithms when the percentage of missing values is high and/or when the number of data points is relatively small. RIFLE is publicly available.

Harnessing Heterogeneity: Learning from Decomposed Feedback in Bayesian Modeling

There is significant interest in learning and optimizing a complex system composed of multiple sub-components, where these components may be agents or autonomous sensors. Among the rich literature on this topic, agent-based and domain-specific simulations can capture complex dynamics and subgroup interaction, but optimizing over such simulations can be computationally and algorithmically challenging. Bayesian approaches, such as Gaussian processes (GPs), can be used to learn a computationally tractable approximation to the underlying dynamics but typically neglect the detailed information about subgroups in the complicated system. We attempt to find the best of both worlds by proposing the idea of decomposed feedback, which captures group-based heterogeneity and dynamics. We introduce a novel decomposed GP regression to incorporate the subgroup decomposed feedback. Our modified regression has provably lower variance -- and thus a more accurate posterior -- compared to previous approaches; it also allows us to introduce a decomposed GP-UCB optimization algorithm that leverages subgroup feedback. The Bayesian nature of our method makes the optimization algorithm trackable with a theoretical guarantee on convergence and no-regret property. To demonstrate the wide applicability of this work, we execute our algorithm on two disparate social problems: infectious disease control in a heterogeneous population and allocation of distributed weather sensors. Experimental results show that our new method provides significant improvement compared to the state-of-the-art.