Rakesh Pavan
FERMI: Fair Empirical Risk Minimization via Exponential Rényi Mutual Information
Feb 24, 2021
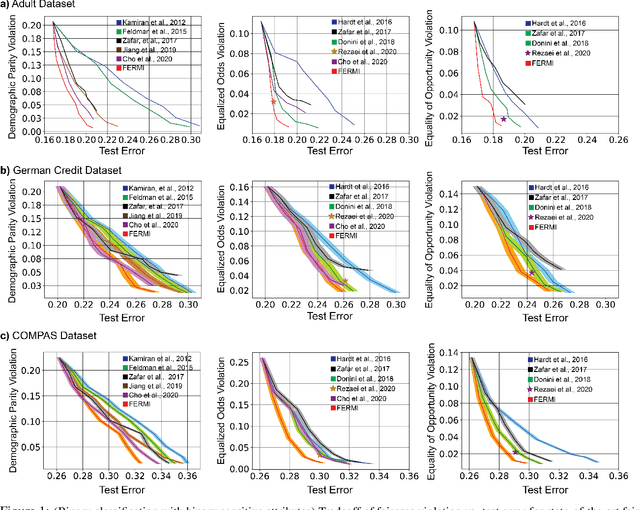
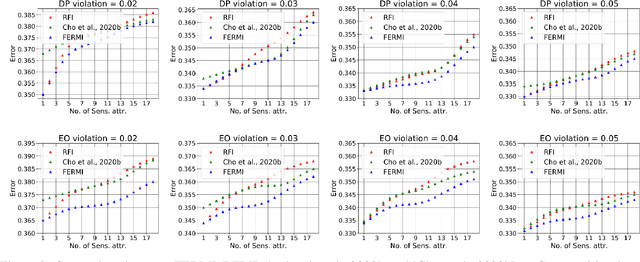
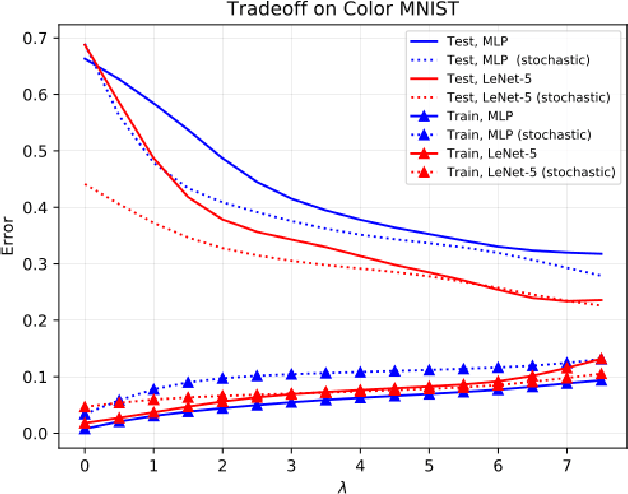
Abstract:In this paper, we propose a new notion of fairness violation, called Exponential R\'enyi Mutual Information (ERMI). We show that ERMI is a strong fairness violation notion in the sense that it provides upper bound guarantees on existing notions of fairness violation. We then propose the Fair Empirical Risk Minimization via ERMI regularization framework, called FERMI. Whereas most existing in-processing fairness algorithms are deterministic, we provide the first stochastic optimization method with a provable convergence guarantee for solving FERMI. Our stochastic algorithm is amenable to large-scale problems, as we demonstrate experimentally. In addition, we provide a batch (deterministic) algorithm for solving FERMI with the optimal rate of convergence. Both of our algorithms are applicable to problems with multiple (non-binary) sensitive attributes and non-binary targets. Extensive experiments show that FERMI achieves the most favorable tradeoffs between fairness violation and test accuracy across various problem setups compared with state-of-the-art baselines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge