FlowCritic: Bridging Value Estimation with Flow Matching in Reinforcement Learning

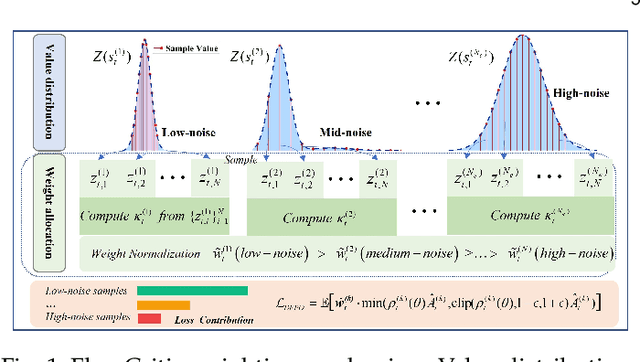
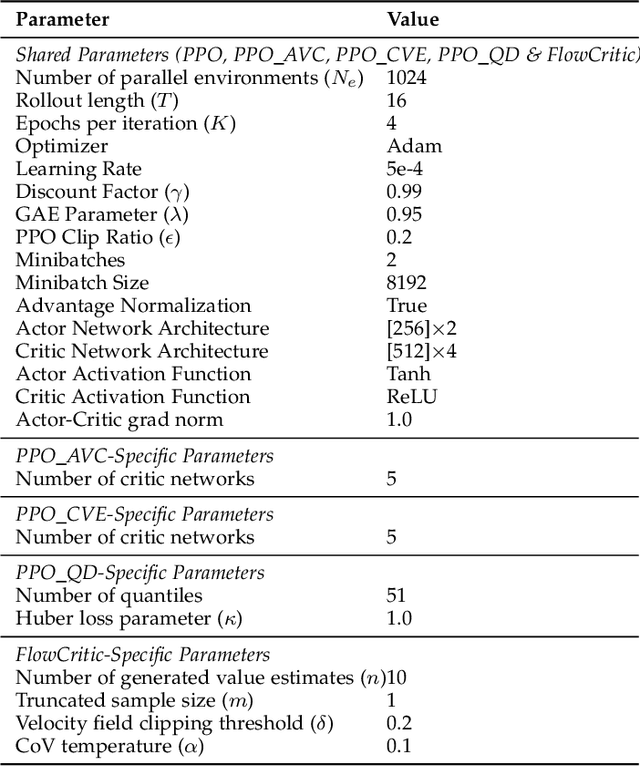
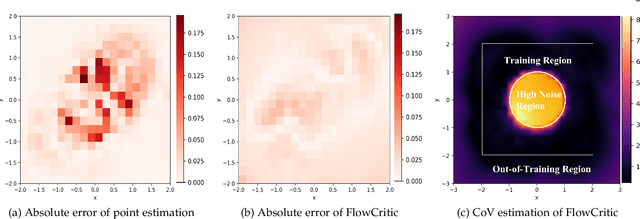
Reliable value estimation serves as the cornerstone of reinforcement learning (RL) by evaluating long-term returns and guiding policy improvement, significantly influencing the convergence speed and final performance. Existing works improve the reliability of value function estimation via multi-critic ensembles and distributional RL, yet the former merely combines multi point estimation without capturing distributional information, whereas the latter relies on discretization or quantile regression, limiting the expressiveness of complex value distributions. Inspired by flow matching's success in generative modeling, we propose a generative paradigm for value estimation, named FlowCritic. Departing from conventional regression for deterministic value prediction, FlowCritic leverages flow matching to model value distributions and generate samples for value estimation.

One Policy but Many Worlds: A Scalable Unified Policy for Versatile Humanoid Locomotion

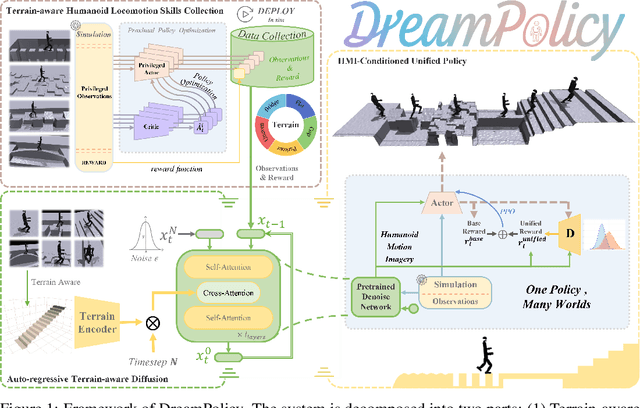
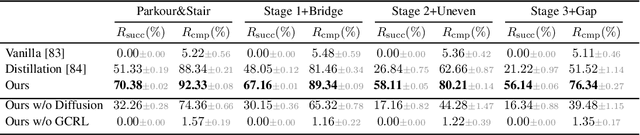
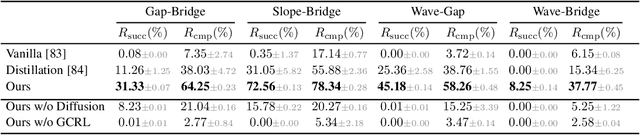
Humanoid locomotion faces a critical scalability challenge: traditional reinforcement learning (RL) methods require task-specific rewards and struggle to leverage growing datasets, even as more training terrains are introduced. We propose DreamPolicy, a unified framework that enables a single policy to master diverse terrains and generalize zero-shot to unseen scenarios by systematically integrating offline data and diffusion-driven motion synthesis. At its core, DreamPolicy introduces Humanoid Motion Imagery (HMI) - future state predictions synthesized through an autoregressive terrain-aware diffusion planner curated by aggregating rollouts from specialized policies across various distinct terrains. Unlike human motion datasets requiring laborious retargeting, our data directly captures humanoid kinematics, enabling the diffusion planner to synthesize "dreamed" trajectories that encode terrain-specific physical constraints. These trajectories act as dynamic objectives for our HMI-conditioned policy, bypassing manual reward engineering and enabling cross-terrain generalization. DreamPolicy addresses the scalability limitations of prior methods: while traditional RL fails to exploit growing datasets, our framework scales seamlessly with more offline data. As the dataset expands, the diffusion prior learns richer locomotion skills, which the policy leverages to master new terrains without retraining. Experiments demonstrate that DreamPolicy achieves average 90% success rates in training environments and an average of 20% higher success on unseen terrains than the prevalent method. It also generalizes to perturbed and composite scenarios where prior approaches collapse. By unifying offline data, diffusion-based trajectory synthesis, and policy optimization, DreamPolicy overcomes the "one task, one policy" bottleneck, establishing a paradigm for scalable, data-driven humanoid control.

GenPO: Generative Diffusion Models Meet On-Policy Reinforcement Learning

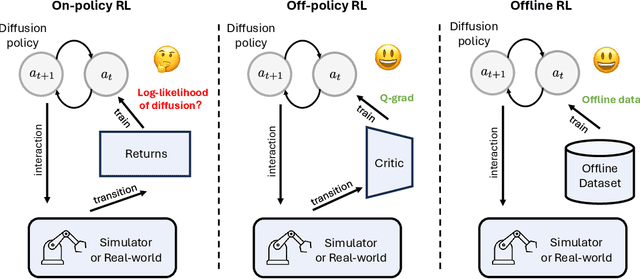
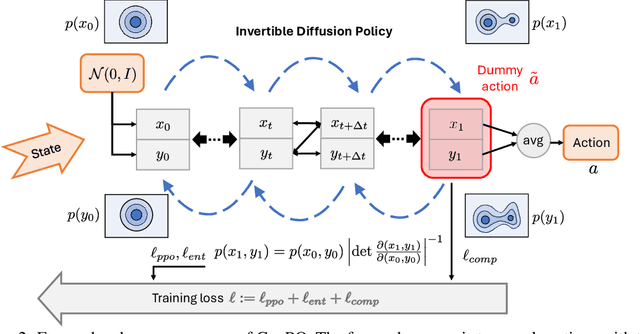
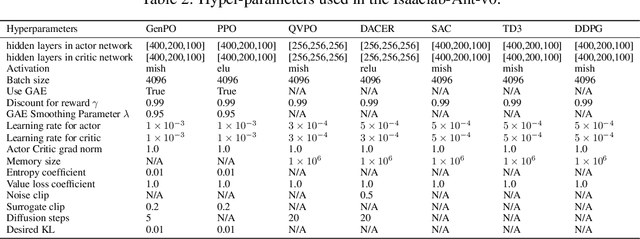
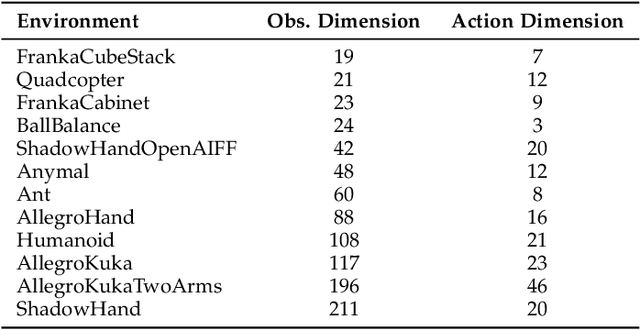
Recent advances in reinforcement learning (RL) have demonstrated the powerful exploration capabilities and multimodality of generative diffusion-based policies. While substantial progress has been made in offline RL and off-policy RL settings, integrating diffusion policies into on-policy frameworks like PPO remains underexplored. This gap is particularly significant given the widespread use of large-scale parallel GPU-accelerated simulators, such as IsaacLab, which are optimized for on-policy RL algorithms and enable rapid training of complex robotic tasks. A key challenge lies in computing state-action log-likelihoods under diffusion policies, which is straightforward for Gaussian policies but intractable for flow-based models due to irreversible forward-reverse processes and discretization errors (e.g., Euler-Maruyama approximations). To bridge this gap, we propose GenPO, a generative policy optimization framework that leverages exact diffusion inversion to construct invertible action mappings. GenPO introduces a novel doubled dummy action mechanism that enables invertibility via alternating updates, resolving log-likelihood computation barriers. Furthermore, we also use the action log-likelihood for unbiased entropy and KL divergence estimation, enabling KL-adaptive learning rates and entropy regularization in on-policy updates. Extensive experiments on eight IsaacLab benchmarks, including legged locomotion (Ant, Humanoid, Anymal-D, Unitree H1, Go2), dexterous manipulation (Shadow Hand), aerial control (Quadcopter), and robotic arm tasks (Franka), demonstrate GenPO's superiority over existing RL baselines. Notably, GenPO is the first method to successfully integrate diffusion policies into on-policy RL, unlocking their potential for large-scale parallelized training and real-world robotic deployment.

Diffusion-based Reinforcement Learning via Q-weighted Variational Policy Optimization

Diffusion models have garnered widespread attention in Reinforcement Learning (RL) for their powerful expressiveness and multimodality. It has been verified that utilizing diffusion policies can significantly improve the performance of RL algorithms in continuous control tasks by overcoming the limitations of unimodal policies, such as Gaussian policies, and providing the agent with enhanced exploration capabilities. However, existing works mainly focus on the application of diffusion policies in offline RL, while their incorporation into online RL is less investigated. The training objective of the diffusion model, known as the variational lower bound, cannot be optimized directly in online RL due to the unavailability of 'good' actions. This leads to difficulties in conducting diffusion policy improvement. To overcome this, we propose a novel model-free diffusion-based online RL algorithm, Q-weighted Variational Policy Optimization (QVPO). Specifically, we introduce the Q-weighted variational loss, which can be proved to be a tight lower bound of the policy objective in online RL under certain conditions. To fulfill these conditions, the Q-weight transformation functions are introduced for general scenarios. Additionally, to further enhance the exploration capability of the diffusion policy, we design a special entropy regularization term. We also develop an efficient behavior policy to enhance sample efficiency by reducing the variance of the diffusion policy during online interactions. Consequently, the QVPO algorithm leverages the exploration capabilities and multimodality of diffusion policies, preventing the RL agent from converging to a sub-optimal policy. To verify the effectiveness of QVPO, we conduct comprehensive experiments on MuJoCo benchmarks. The final results demonstrate that QVPO achieves state-of-the-art performance on both cumulative reward and sample efficiency.

Guidance with Spherical Gaussian Constraint for Conditional Diffusion

Recent advances in diffusion models attempt to handle conditional generative tasks by utilizing a differentiable loss function for guidance without the need for additional training. While these methods achieved certain success, they often compromise on sample quality and require small guidance step sizes, leading to longer sampling processes. This paper reveals that the fundamental issue lies in the manifold deviation during the sampling process when loss guidance is employed. We theoretically show the existence of manifold deviation by establishing a certain lower bound for the estimation error of the loss guidance. To mitigate this problem, we propose Diffusion with Spherical Gaussian constraint (DSG), drawing inspiration from the concentration phenomenon in high-dimensional Gaussian distributions. DSG effectively constrains the guidance step within the intermediate data manifold through optimization and enables the use of larger guidance steps. Furthermore, we present a closed-form solution for DSG denoising with the Spherical Gaussian constraint. Notably, DSG can seamlessly integrate as a plugin module within existing training-free conditional diffusion methods. Implementing DSG merely involves a few lines of additional code with almost no extra computational overhead, yet it leads to significant performance improvements. Comprehensive experimental results in various conditional generation tasks validate the superiority and adaptability of DSG in terms of both sample quality and time efficiency.

Reduced Policy Optimization for Continuous Control with Hard Constraints

Recent advances in constrained reinforcement learning (RL) have endowed reinforcement learning with certain safety guarantees. However, deploying existing constrained RL algorithms in continuous control tasks with general hard constraints remains challenging, particularly in those situations with non-convex hard constraints. Inspired by the generalized reduced gradient (GRG) algorithm, a classical constrained optimization technique, we propose a reduced policy optimization (RPO) algorithm that combines RL with GRG to address general hard constraints. RPO partitions actions into basic actions and nonbasic actions following the GRG method and outputs the basic actions via a policy network. Subsequently, RPO calculates the nonbasic actions by solving equations based on equality constraints using the obtained basic actions. The policy network is then updated by implicitly differentiating nonbasic actions with respect to basic actions. Additionally, we introduce an action projection procedure based on the reduced gradient and apply a modified Lagrangian relaxation technique to ensure inequality constraints are satisfied. To the best of our knowledge, RPO is the first attempt that introduces GRG to RL as a way of efficiently handling both equality and inequality hard constraints. It is worth noting that there is currently a lack of RL environments with complex hard constraints, which motivates us to develop three new benchmarks: two robotics manipulation tasks and a smart grid operation control task. With these benchmarks, RPO achieves better performance than previous constrained RL algorithms in terms of both cumulative reward and constraint violation. We believe RPO, along with the new benchmarks, will open up new opportunities for applying RL to real-world problems with complex constraints.

Two Sides of The Same Coin: Bridging Deep Equilibrium Models and Neural ODEs via Homotopy Continuation

Deep Equilibrium Models (DEQs) and Neural Ordinary Differential Equations (Neural ODEs) are two branches of implicit models that have achieved remarkable success owing to their superior performance and low memory consumption. While both are implicit models, DEQs and Neural ODEs are derived from different mathematical formulations. Inspired by homotopy continuation, we establish a connection between these two models and illustrate that they are actually two sides of the same coin. Homotopy continuation is a classical method of solving nonlinear equations based on a corresponding ODE. Given this connection, we proposed a new implicit model called HomoODE that inherits the property of high accuracy from DEQs and the property of stability from Neural ODEs. Unlike DEQs, which explicitly solve an equilibrium-point-finding problem via Newton's methods in the forward pass, HomoODE solves the equilibrium-point-finding problem implicitly using a modified Neural ODE via homotopy continuation. Further, we developed an acceleration method for HomoODE with a shared learnable initial point. It is worth noting that our model also provides a better understanding of why Augmented Neural ODEs work as long as the augmented part is regarded as the equilibrium point to find. Comprehensive experiments with several image classification tasks demonstrate that HomoODE surpasses existing implicit models in terms of both accuracy and memory consumption.