Generalization and Risk Bounds for Recurrent Neural Networks

Recurrent Neural Networks (RNNs) have achieved great success in the prediction of sequential data. However, their theoretical studies are still lagging behind because of their complex interconnected structures. In this paper, we establish a new generalization error bound for vanilla RNNs, and provide a unified framework to calculate the Rademacher complexity that can be applied to a variety of loss functions. When the ramp loss is used, we show that our bound is tighter than the existing bounds based on the same assumptions on the Frobenius and spectral norms of the weight matrices and a few mild conditions. Our numerical results show that our new generalization bound is the tightest among all existing bounds in three public datasets. Our bound improves the second tightest one by an average percentage of 13.80% and 3.01% when the $\tanh$ and ReLU activation functions are used, respectively. Moreover, we derive a sharp estimation error bound for RNN-based estimators obtained through empirical risk minimization (ERM) in multi-class classification problems when the loss function satisfies a Bernstein condition.

Statistical Inference For Noisy Matrix Completion Incorporating Auxiliary Information

This paper investigates statistical inference for noisy matrix completion in a semi-supervised model when auxiliary covariates are available. The model consists of two parts. One part is a low-rank matrix induced by unobserved latent factors; the other part models the effects of the observed covariates through a coefficient matrix which is composed of high-dimensional column vectors. We model the observational pattern of the responses through a logistic regression of the covariates, and allow its probability to go to zero as the sample size increases. We apply an iterative least squares (LS) estimation approach in our considered context. The iterative LS methods in general enjoy a low computational cost, but deriving the statistical properties of the resulting estimators is a challenging task. We show that our method only needs a few iterations, and the resulting entry-wise estimators of the low-rank matrix and the coefficient matrix are guaranteed to have asymptotic normal distributions. As a result, individual inference can be conducted for each entry of the unknown matrices. We also propose a simultaneous testing procedure with multiplier bootstrap for the high-dimensional coefficient matrix. This simultaneous inferential tool can help us further investigate the effects of covariates for the prediction of missing entries.

SleepEGAN: A GAN-enhanced Ensemble Deep Learning Model for Imbalanced Classification of Sleep Stages

Deep neural networks have played an important role in automatic sleep stage classification because of their strong representation and in-model feature transformation abilities. However, class imbalance and individual heterogeneity which typically exist in raw EEG signals of sleep data can significantly affect the classification performance of any machine learning algorithms. To solve these two problems, this paper develops a generative adversarial network (GAN)-powered ensemble deep learning model, named SleepEGAN, for the imbalanced classification of sleep stages. To alleviate class imbalance, we propose a new GAN (called EGAN) architecture adapted to the features of EEG signals for data augmentation. The generated samples for the minority classes are used in the training process. In addition, we design a cost-free ensemble learning strategy to reduce the model estimation variance caused by the heterogeneity between the validation and test sets, so as to enhance the accuracy and robustness of prediction performance. We show that the proposed method can improve classification accuracy compared to several existing state-of-the-art methods using three public sleep datasets.

Privacy-Preserving Community Detection for Locally Distributed Multiple Networks

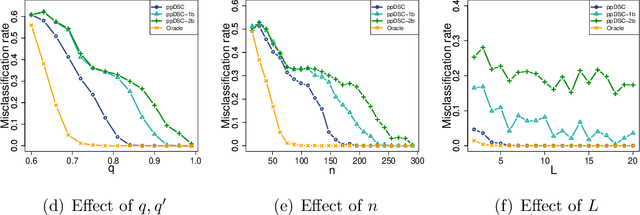
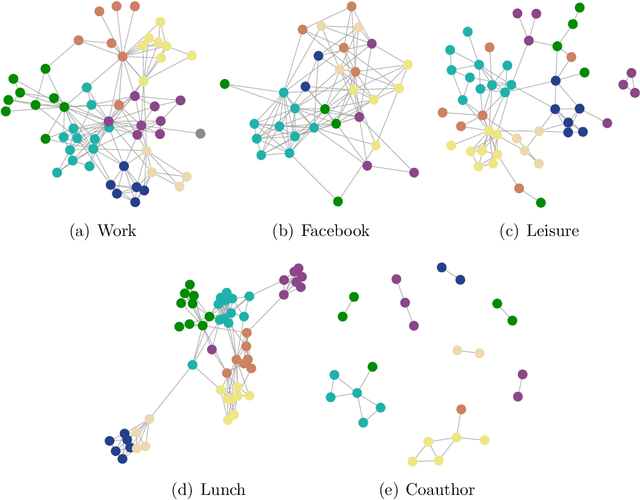
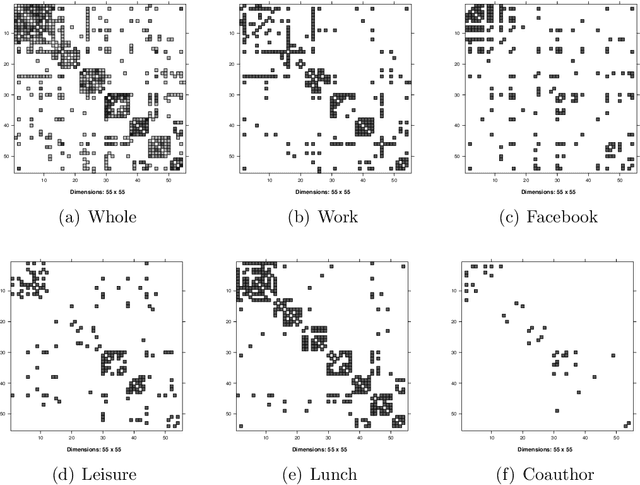
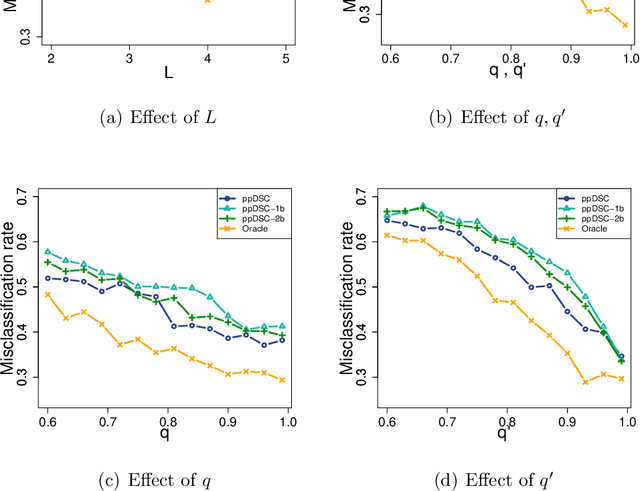
Modern multi-layer networks are commonly stored and analyzed in a local and distributed fashion because of the privacy, ownership, and communication costs. The literature on the model-based statistical methods for community detection based on these data is still limited. This paper proposes a new method for consensus community detection and estimation in a multi-layer stochastic block model using locally stored and computed network data with privacy protection. A novel algorithm named privacy-preserving Distributed Spectral Clustering (ppDSC) is developed. To preserve the edges' privacy, we adopt the randomized response (RR) mechanism to perturb the network edges, which satisfies the strong notion of differential privacy. The ppDSC algorithm is performed on the squared RR-perturbed adjacency matrices to prevent possible cancellation of communities among different layers. To remove the bias incurred by RR and the squared network matrices, we develop a two-step bias-adjustment procedure. Then we perform eigen-decomposition on the debiased matrices, aggregation of the local eigenvectors using an orthogonal Procrustes transformation, and k-means clustering. We provide theoretical analysis on the statistical errors of ppDSC in terms of eigen-vector estimation. In addition, the blessings and curses of network heterogeneity are well-explained by our bounds.

Efficient Estimation of General Treatment Effects using Neural Networks with A Diverging Number of Confounders

The estimation of causal effects is a primary goal of behavioral, social, economic and biomedical sciences. Under the unconfounded treatment assignment condition, adjustment for confounders requires estimating the nuisance functions relating outcome and/or treatment to confounders. The conventional approaches rely on either a parametric or a nonparametric modeling strategy to approximate the nuisance functions. Parametric methods can introduce serious bias into casual effect estimation due to possible mis-specification, while nonparametric estimation suffers from the "curse of dimensionality". This paper proposes a new unified approach for efficient estimation of treatment effects using feedforward artificial neural networks when the number of covariates is allowed to increase with the sample size. We consider a general optimization framework that includes the average, quantile and asymmetric least squares treatment effects as special cases. Under this unified setup, we develop a generalized optimization estimator for the treatment effect with the nuisance function estimated by neural networks. We further establish the consistency and asymptotic normality of the proposed estimator and show that it attains the semiparametric efficiency bound. The proposed methods are illustrated via simulation studies and a real data application.

Multivariate Functional Regression via Nested Reduced-Rank Regularization

We propose a nested reduced-rank regression (NRRR) approach in fitting regression model with multivariate functional responses and predictors, to achieve tailored dimension reduction and facilitate interpretation/visualization of the resulting functional model. Our approach is based on a two-level low-rank structure imposed on the functional regression surfaces. A global low-rank structure identifies a small set of latent principal functional responses and predictors that drives the underlying regression association. A local low-rank structure then controls the complexity and smoothness of the association between the principal functional responses and predictors. Through a basis expansion approach, the functional problem boils down to an interesting integrated matrix approximation task, where the blocks or submatrices of an integrated low-rank matrix share some common row space and/or column space. An iterative algorithm with convergence guarantee is developed. We establish the consistency of NRRR and also show through non-asymptotic analysis that it can achieve at least a comparable error rate to that of the reduced-rank regression. Simulation studies demonstrate the effectiveness of NRRR. We apply NRRR in an electricity demand problem, to relate the trajectories of the daily electricity consumption with those of the daily temperatures.