Statistical Inference For Noisy Matrix Completion Incorporating Auxiliary Information

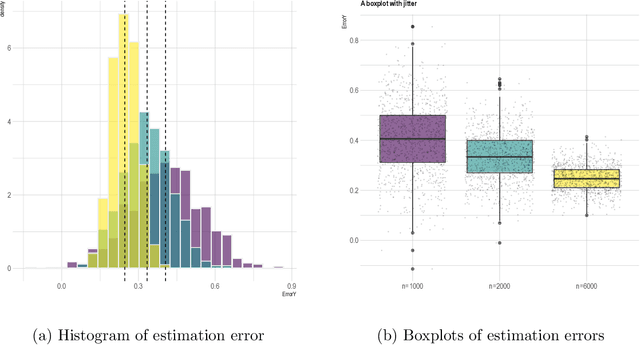
This paper investigates statistical inference for noisy matrix completion in a semi-supervised model when auxiliary covariates are available. The model consists of two parts. One part is a low-rank matrix induced by unobserved latent factors; the other part models the effects of the observed covariates through a coefficient matrix which is composed of high-dimensional column vectors. We model the observational pattern of the responses through a logistic regression of the covariates, and allow its probability to go to zero as the sample size increases. We apply an iterative least squares (LS) estimation approach in our considered context. The iterative LS methods in general enjoy a low computational cost, but deriving the statistical properties of the resulting estimators is a challenging task. We show that our method only needs a few iterations, and the resulting entry-wise estimators of the low-rank matrix and the coefficient matrix are guaranteed to have asymptotic normal distributions. As a result, individual inference can be conducted for each entry of the unknown matrices. We also propose a simultaneous testing procedure with multiplier bootstrap for the high-dimensional coefficient matrix. This simultaneous inferential tool can help us further investigate the effects of covariates for the prediction of missing entries.

Comments on Leo Breiman's paper 'Statistical Modeling: The Two Cultures' , 199-231)

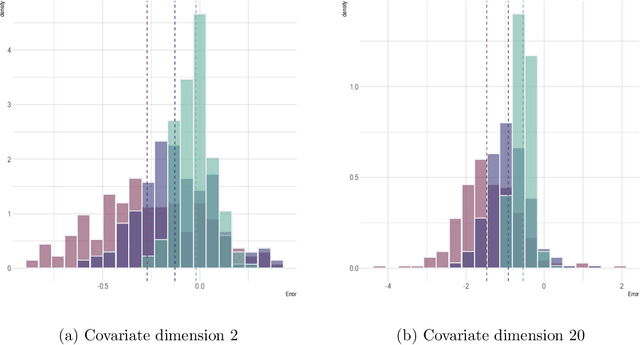
Breiman challenged statisticians to think more broadly, to step into the unknown, model-free learning world, with him paving the way forward. Statistics community responded with slight optimism, some skepticism, and plenty of disbelief. Today, we are at the same crossroad anew. Faced with the enormous practical success of model-free, deep, and machine learning, we are naturally inclined to think that everything is resolved. A new frontier has emerged; the one where the role, impact, or stability of the {\it learning} algorithms is no longer measured by prediction quality, but an inferential one -- asking the questions of {\it why} and {\it if} can no longer be safely ignored.

Minimax Semiparametric Learning With Approximate Sparsity

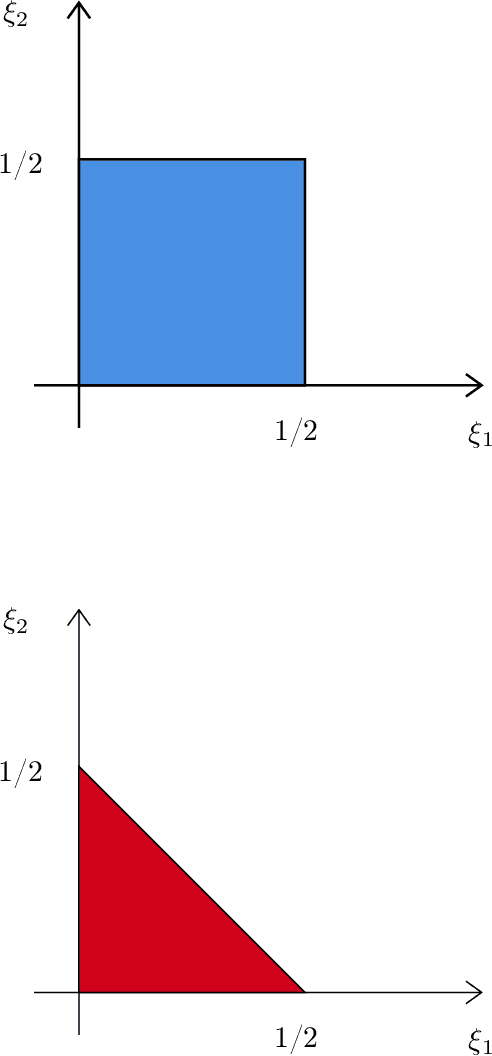
Many objects of interest can be expressed as a linear, mean square continuous functional of a least squares projection (regression). Often the regression may be high dimensional, depending on many variables. This paper gives minimal conditions for root-n consistent and efficient estimation of such objects when the regression and the Riesz representer of the functional are approximately sparse and the sum of the absolute value of the coefficients is bounded. The approximately sparse functions we consider are those where an approximation by some $t$ regressors has root mean square error less than or equal to $Ct^{-\xi}$ for $C,$ $\xi>0.$ We show that a necessary condition for efficient estimation is that the sparse approximation rate $\xi_{1}$ for the regression and the rate $\xi_{2}$ for the Riesz representer satisfy $\max\{\xi_{1} ,\xi_{2}\}>1/2.$ This condition is stronger than the corresponding condition $\xi_{1}+\xi_{2}>1/2$ for Holder classes of functions. We also show that Lasso based, cross-fit, debiased machine learning estimators are asymptotically efficient under these conditions. In addition we show efficiency of an estimator without cross-fitting when the functional depends on the regressors and the regression sparse approximation rate satisfies $\xi_{1}>1/2$.

Exact and Robust Conformal Inference Methods for Predictive Machine Learning With Dependent Data

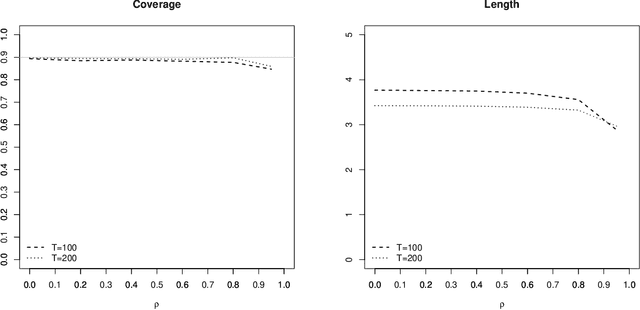
We extend conformal inference to general settings that allow for time series data. Our proposal is developed as a randomization method and accounts for potential serial dependence by including block structures in the permutation scheme. As a result, the proposed method retains the exact, model-free validity when the data are i.i.d. or more generally exchangeable, similar to usual conformal inference methods. When exchangeability fails, as is the case for common time series data, the proposed approach is approximately valid under weak assumptions on the conformity score.

Significance testing in non-sparse high-dimensional linear models

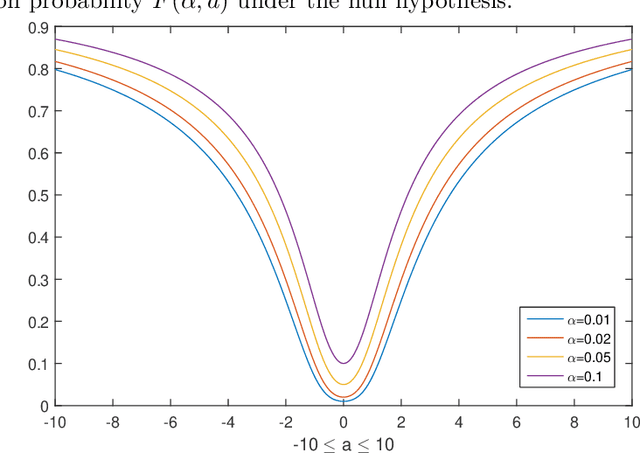
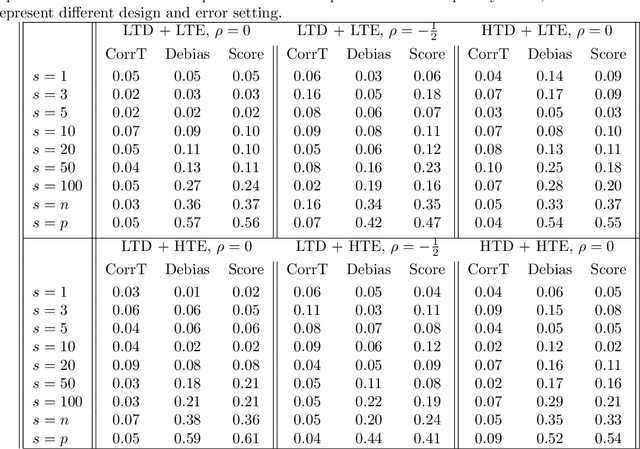
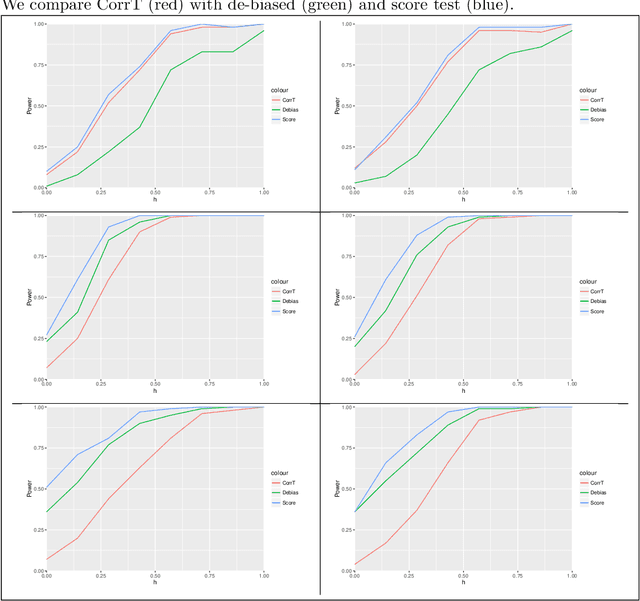
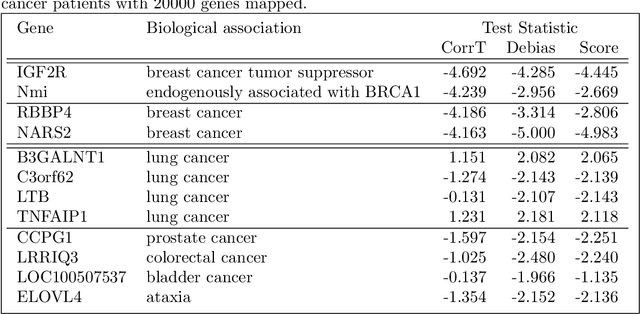
In high-dimensional linear models, the sparsity assumption is typically made, stating that most of the parameters are equal to zero. Under the sparsity assumption, estimation and, recently, inference have been well studied. However, in practice, sparsity assumption is not checkable and more importantly is often violated; a large number of covariates might be expected to be associated with the response, indicating that possibly all, rather than just a few, parameters are non-zero. A natural example is a genome-wide gene expression profiling, where all genes are believed to affect a common disease marker. We show that existing inferential methods are sensitive to the sparsity assumption, and may, in turn, result in the severe lack of control of Type-I error. In this article, we propose a new inferential method, named CorrT, which is robust to model misspecification such as heteroscedasticity and lack of sparsity. CorrT is shown to have Type I error approaching the nominal level for \textit{any} models and Type II error approaching zero for sparse and many dense models. In fact, CorrT is also shown to be optimal in a variety of frameworks: sparse, non-sparse and hybrid models where sparse and dense signals are mixed. Numerical experiments show a favorable performance of the CorrT test compared to the state-of-the-art methods.

Breaking the curse of dimensionality in regression

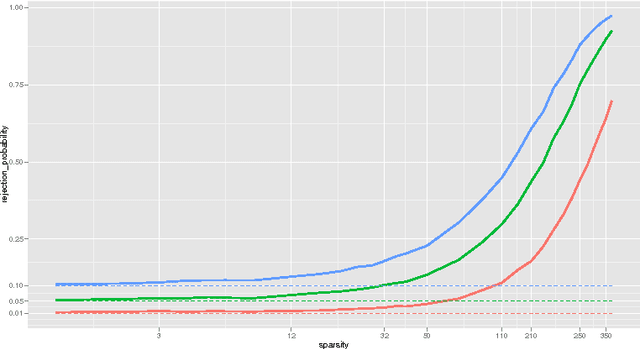
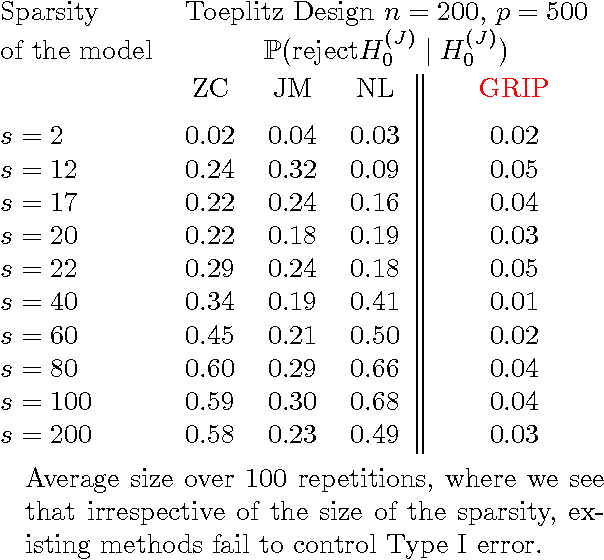
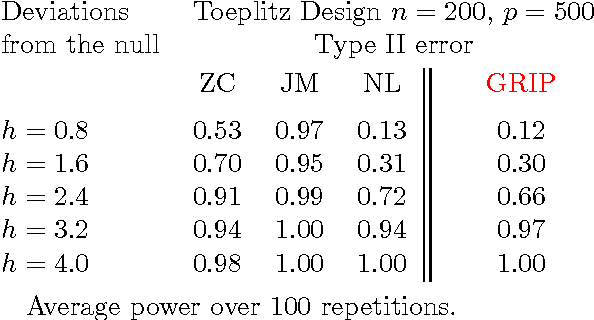
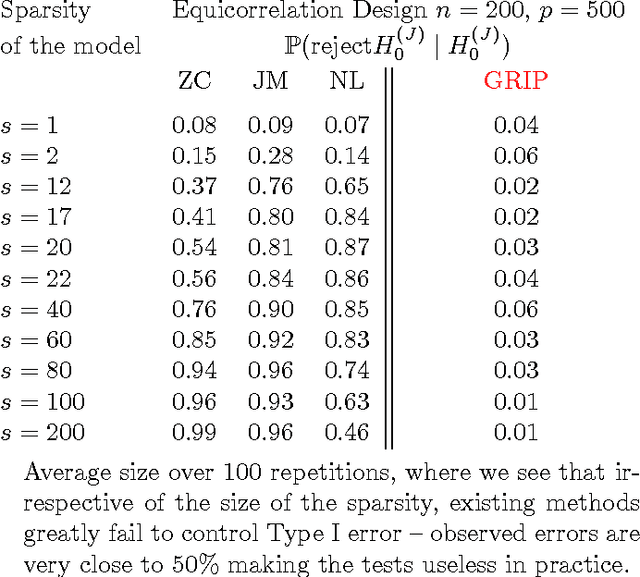
Models with many signals, high-dimensional models, often impose structures on the signal strengths. The common assumption is that only a few signals are strong and most of the signals are zero or close (collectively) to zero. However, such a requirement might not be valid in many real-life applications. In this article, we are interested in conducting large-scale inference in models that might have signals of mixed strengths. The key challenge is that the signals that are not under testing might be collectively non-negligible (although individually small) and cannot be accurately learned. This article develops a new class of tests that arise from a moment matching formulation. A virtue of these moment-matching statistics is their ability to borrow strength across features, adapt to the sparsity size and exert adjustment for testing growing number of hypothesis. GRoup-level Inference of Parameter, GRIP, test harvests effective sparsity structures with hypothesis formulation for an efficient multiple testing procedure. Simulated data showcase that GRIPs error control is far better than the alternative methods. We develop a minimax theory, demonstrating optimality of GRIP for a broad range of models, including those where the model is a mixture of a sparse and high-dimensional dense signals.

Comments on `High-dimensional simultaneous inference with the bootstrap'

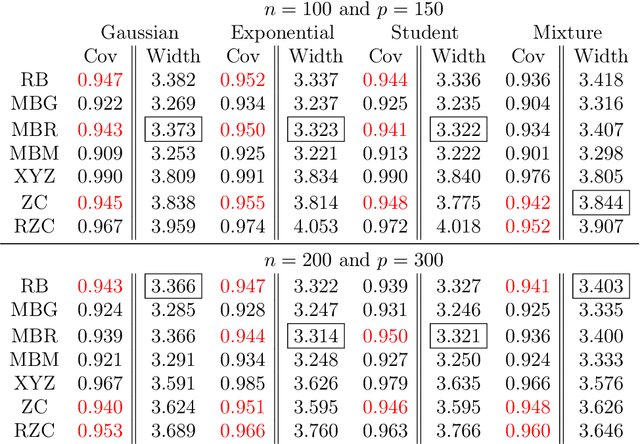
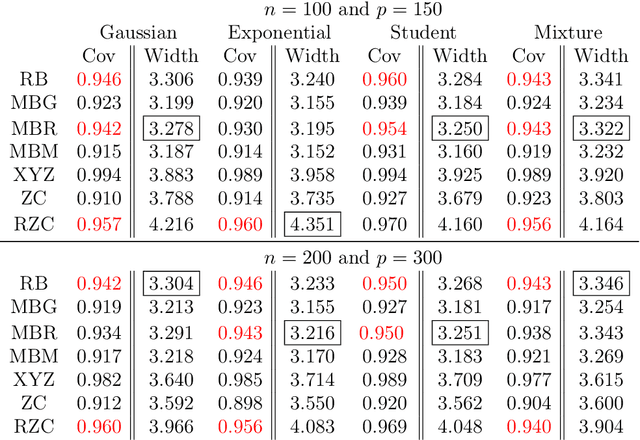
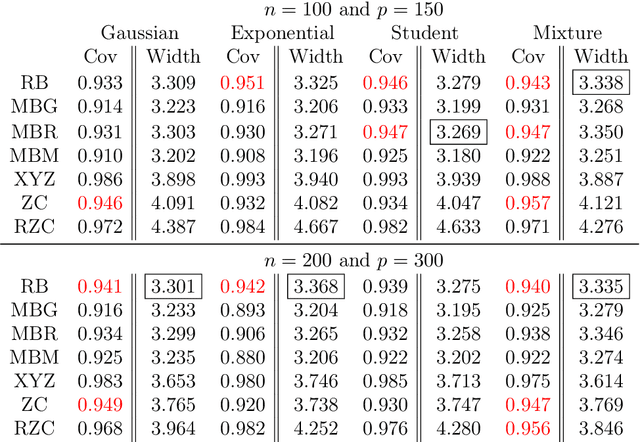
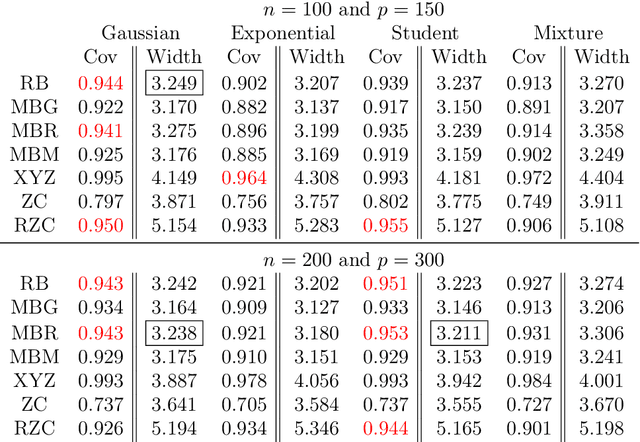
We provide comments on the article "High-dimensional simultaneous inference with the bootstrap" by Ruben Dezeure, Peter Buhlmann and Cun-Hui Zhang.

A projection pursuit framework for testing general high-dimensional hypothesis

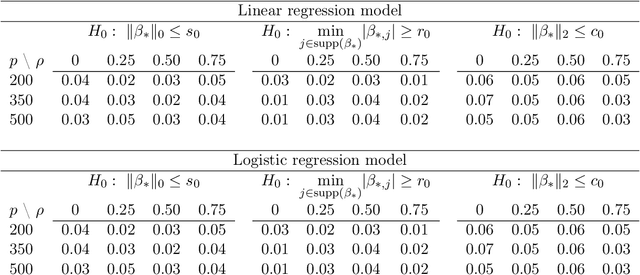
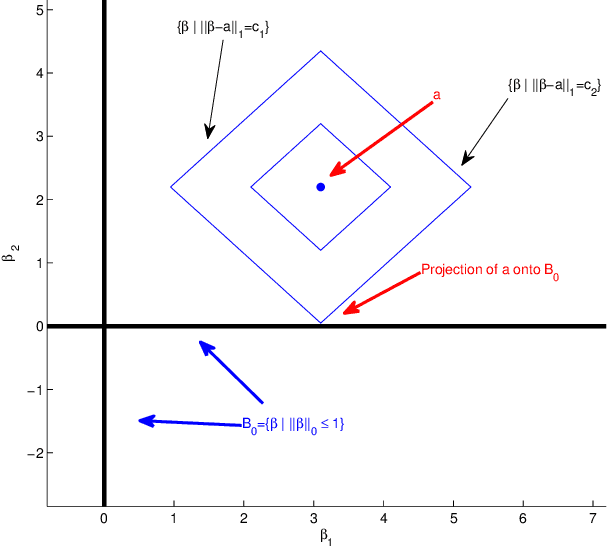
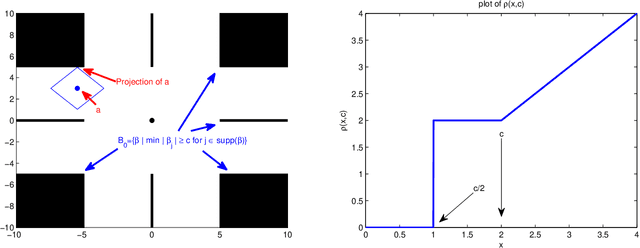
This article develops a framework for testing general hypothesis in high-dimensional models where the number of variables may far exceed the number of observations. Existing literature has considered less than a handful of hypotheses, such as testing individual coordinates of the model parameter. However, the problem of testing general and complex hypotheses remains widely open. We propose a new inference method developed around the hypothesis adaptive projection pursuit framework, which solves the testing problems in the most general case. The proposed inference is centered around a new class of estimators defined as $l_1$ projection of the initial guess of the unknown onto the space defined by the null. This projection automatically takes into account the structure of the null hypothesis and allows us to study formal inference for a number of long-standing problems. For example, we can directly conduct inference on the sparsity level of the model parameters and the minimum signal strength. This is especially significant given the fact that the former is a fundamental condition underlying most of the theoretical development in high-dimensional statistics, while the latter is a key condition used to establish variable selection properties. Moreover, the proposed method is asymptotically exact and has satisfactory power properties for testing very general functionals of the high-dimensional parameters. The simulation studies lend further support to our theoretical claims and additionally show excellent finite-sample size and power properties of the proposed test.

Linear Hypothesis Testing in Dense High-Dimensional Linear Models

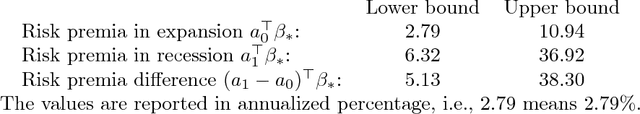
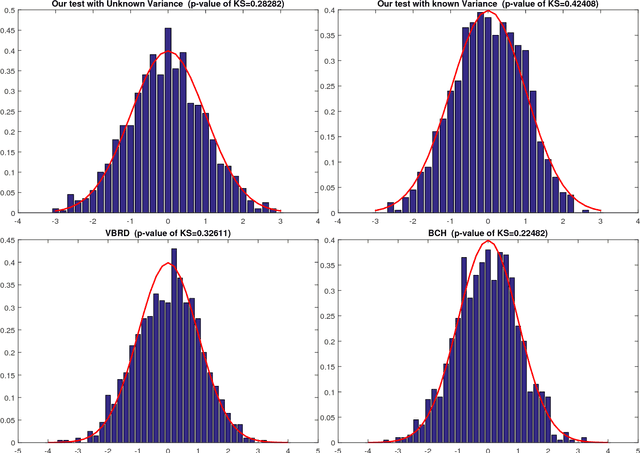
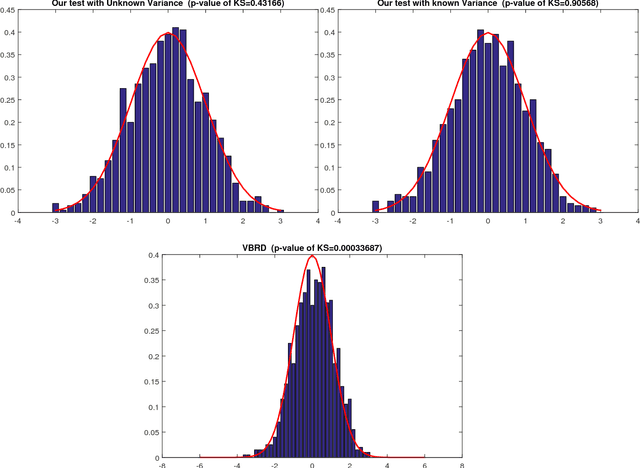
We propose a methodology for testing linear hypothesis in high-dimensional linear models. The proposed test does not impose any restriction on the size of the model, i.e. model sparsity or the loading vector representing the hypothesis. Providing asymptotically valid methods for testing general linear functions of the regression parameters in high-dimensions is extremely challenging -- especially without making restrictive or unverifiable assumptions on the number of non-zero elements. We propose to test the moment conditions related to the newly designed restructured regression, where the inputs are transformed and augmented features. These new features incorporate the structure of the null hypothesis directly. The test statistics are constructed in such a way that lack of sparsity in the original model parameter does not present a problem for the theoretical justification of our procedures. We establish asymptotically exact control on Type I error without imposing any sparsity assumptions on model parameter or the vector representing the linear hypothesis. Our method is also shown to achieve certain optimality in detecting deviations from the null hypothesis. We demonstrate the favorable finite-sample performance of the proposed methods, via a number of numerical and a real data example.

Two-sample testing in non-sparse high-dimensional linear models

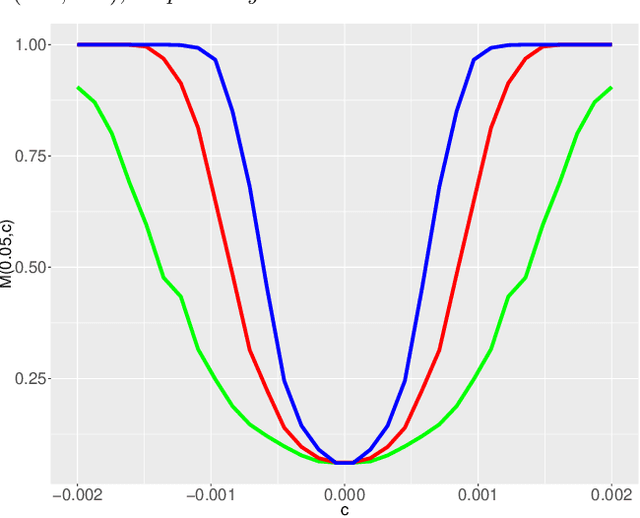
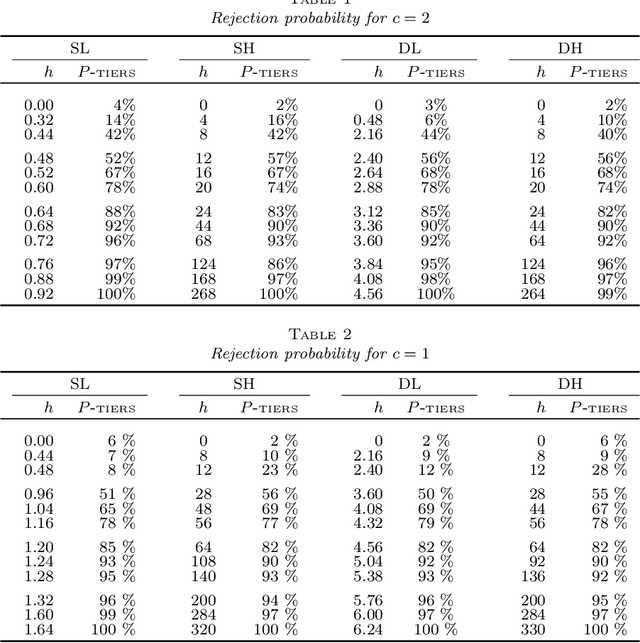
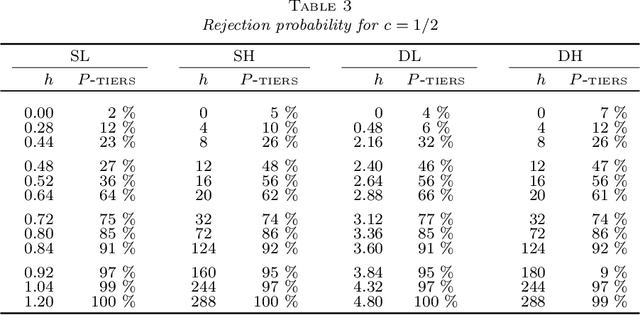
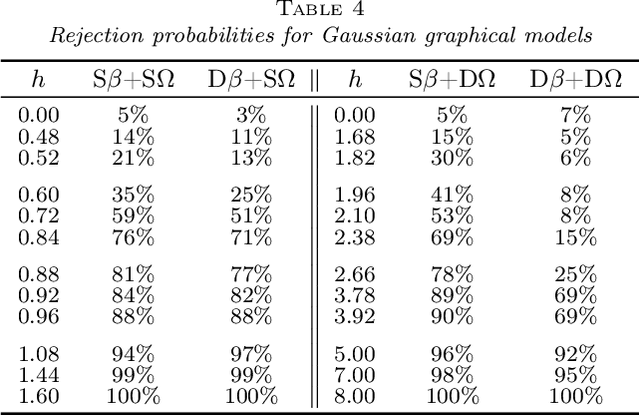
In analyzing high-dimensional models, sparsity of the model parameter is a common but often undesirable assumption. In this paper, we study the following two-sample testing problem: given two samples generated by two high-dimensional linear models, we aim to test whether the regression coefficients of the two linear models are identical. We propose a framework named TIERS (short for TestIng Equality of Regression Slopes), which solves the two-sample testing problem without making any assumptions on the sparsity of the regression parameters. TIERS builds a new model by convolving the two samples in such a way that the original hypothesis translates into a new moment condition. A self-normalization construction is then developed to form a moment test. We provide rigorous theory for the developed framework. Under very weak conditions of the feature covariance, we show that the accuracy of the proposed test in controlling Type I errors is robust both to the lack of sparsity in the features and to the heavy tails in the error distribution, even when the sample size is much smaller than the feature dimension. Moreover, we discuss minimax optimality and efficiency properties of the proposed test. Simulation analysis demonstrates excellent finite-sample performance of our test. In deriving the test, we also develop tools that are of independent interest. The test is built upon a novel estimator, called Auto-aDaptive Dantzig Selector (ADDS), which not only automatically chooses an appropriate scale of the error term but also incorporates prior information. To effectively approximate the critical value of the test statistic, we develop a novel high-dimensional plug-in approach that complements the recent advances in Gaussian approximation theory.