RieszNet and ForestRiesz: Automatic Debiased Machine Learning with Neural Nets and Random Forests

Many causal and policy effects of interest are defined by linear functionals of high-dimensional or non-parametric regression functions. $\sqrt{n}$-consistent and asymptotically normal estimation of the object of interest requires debiasing to reduce the effects of regularization and/or model selection on the object of interest. Debiasing is typically achieved by adding a correction term to the plug-in estimator of the functional, that is derived based on a functional-specific theoretical derivation of what is known as the influence function and which leads to properties such as double robustness and Neyman orthogonality. We instead implement an automatic debiasing procedure based on automatically learning the Riesz representation of the linear functional using Neural Nets and Random Forests. Our method solely requires value query oracle access to the linear functional. We propose a multi-tasking Neural Net debiasing method with stochastic gradient descent minimization of a combined Riesz representer and regression loss, while sharing representation layers for the two functions. We also propose a Random Forest method which learns a locally linear representation of the Riesz function. Even though our methodology applies to arbitrary functionals, we experimentally find that it beats state of the art performance of the prior neural net based estimator of Shi et al. (2019) for the case of the average treatment effect functional. We also evaluate our method on the more challenging problem of estimating average marginal effects with continuous treatments, using semi-synthetic data of gasoline price changes on gasoline demand.

A Simple and General Debiased Machine Learning Theorem with Finite Sample Guarantees

Debiased machine learning is a meta algorithm based on bias correction and sample splitting to calculate confidence intervals for functionals (i.e. scalar summaries) of machine learning algorithms. For example, an analyst may desire the confidence interval for a treatment effect estimated with a neural network. We provide a nonasymptotic debiased machine learning theorem that encompasses any global or local functional of any machine learning algorithm that satisfies a few simple, interpretable conditions. Formally, we prove consistency, Gaussian approximation, and semiparametric efficiency by finite sample arguments. The rate of convergence is root-n for global functionals, and it degrades gracefully for local functionals. Our results culminate in a simple set of conditions that an analyst can use to translate modern learning theory rates into traditional statistical inference. The conditions reveal a new double robustness property for ill posed inverse problems.

Minimax Semiparametric Learning With Approximate Sparsity

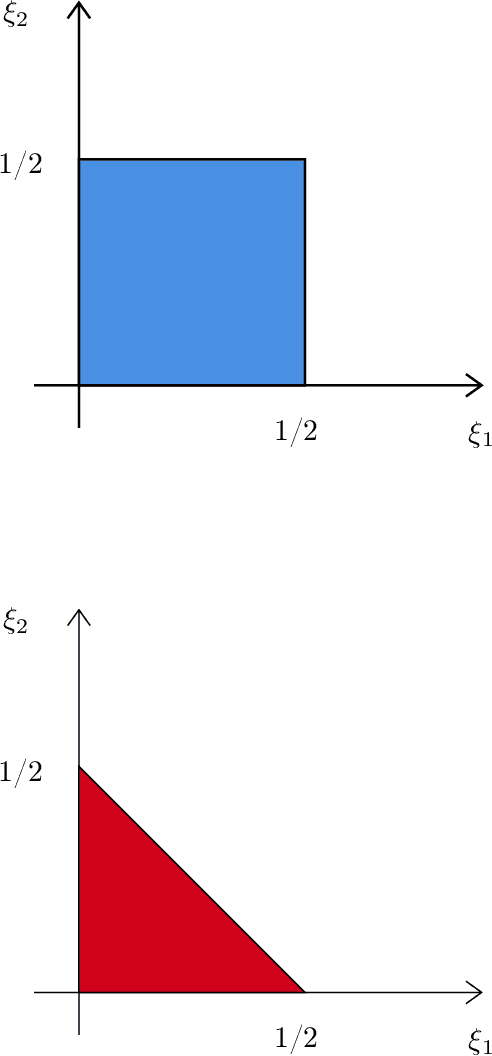
Many objects of interest can be expressed as a linear, mean square continuous functional of a least squares projection (regression). Often the regression may be high dimensional, depending on many variables. This paper gives minimal conditions for root-n consistent and efficient estimation of such objects when the regression and the Riesz representer of the functional are approximately sparse and the sum of the absolute value of the coefficients is bounded. The approximately sparse functions we consider are those where an approximation by some $t$ regressors has root mean square error less than or equal to $Ct^{-\xi}$ for $C,$ $\xi>0.$ We show that a necessary condition for efficient estimation is that the sparse approximation rate $\xi_{1}$ for the regression and the rate $\xi_{2}$ for the Riesz representer satisfy $\max\{\xi_{1} ,\xi_{2}\}>1/2.$ This condition is stronger than the corresponding condition $\xi_{1}+\xi_{2}>1/2$ for Holder classes of functions. We also show that Lasso based, cross-fit, debiased machine learning estimators are asymptotically efficient under these conditions. In addition we show efficiency of an estimator without cross-fitting when the functional depends on the regressors and the regression sparse approximation rate satisfies $\xi_{1}>1/2$.