Minimax Semiparametric Learning With Approximate Sparsity
Paper and Code
Dec 27, 2019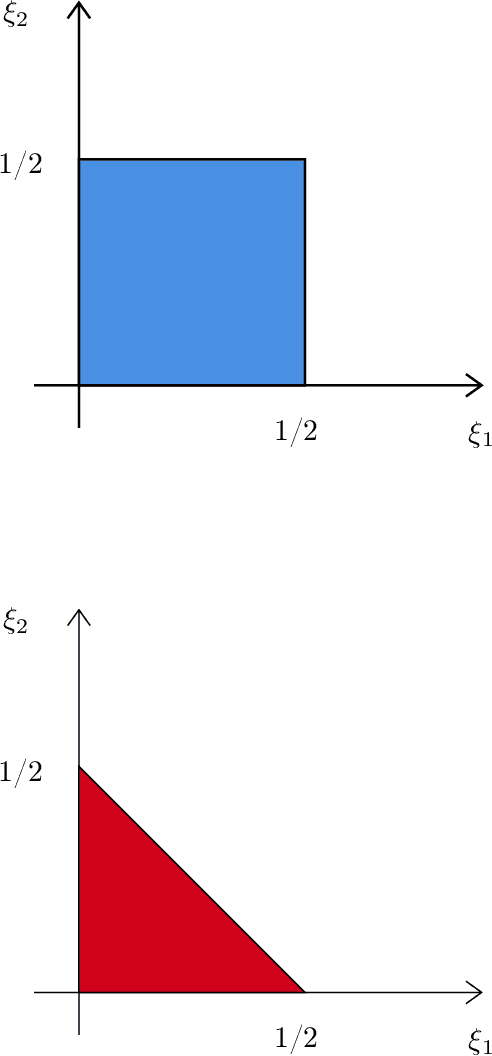
Many objects of interest can be expressed as a linear, mean square continuous functional of a least squares projection (regression). Often the regression may be high dimensional, depending on many variables. This paper gives minimal conditions for root-n consistent and efficient estimation of such objects when the regression and the Riesz representer of the functional are approximately sparse and the sum of the absolute value of the coefficients is bounded. The approximately sparse functions we consider are those where an approximation by some $t$ regressors has root mean square error less than or equal to $Ct^{-\xi}$ for $C,$ $\xi>0.$ We show that a necessary condition for efficient estimation is that the sparse approximation rate $\xi_{1}$ for the regression and the rate $\xi_{2}$ for the Riesz representer satisfy $\max\{\xi_{1} ,\xi_{2}\}>1/2.$ This condition is stronger than the corresponding condition $\xi_{1}+\xi_{2}>1/2$ for Holder classes of functions. We also show that Lasso based, cross-fit, debiased machine learning estimators are asymptotically efficient under these conditions. In addition we show efficiency of an estimator without cross-fitting when the functional depends on the regressors and the regression sparse approximation rate satisfies $\xi_{1}>1/2$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge