Privacy-Preserving Community Detection for Locally Distributed Multiple Networks
Paper and Code
Jun 27, 2023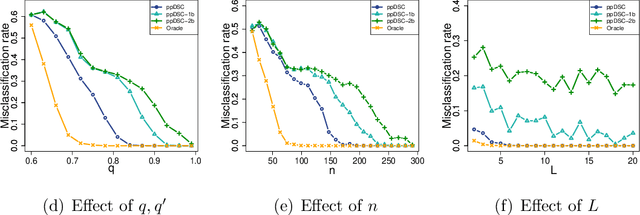
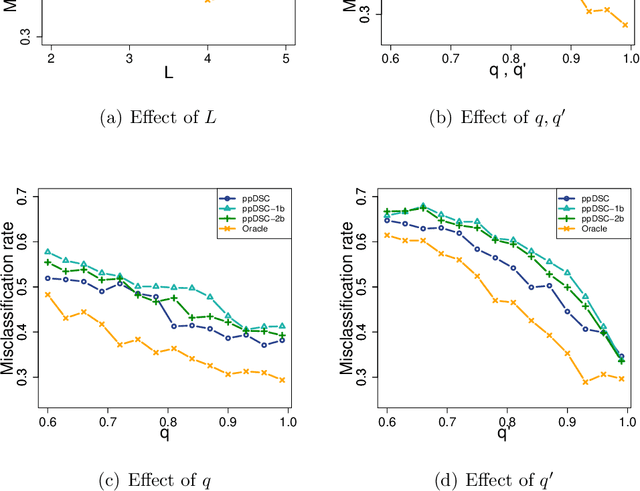
Modern multi-layer networks are commonly stored and analyzed in a local and distributed fashion because of the privacy, ownership, and communication costs. The literature on the model-based statistical methods for community detection based on these data is still limited. This paper proposes a new method for consensus community detection and estimation in a multi-layer stochastic block model using locally stored and computed network data with privacy protection. A novel algorithm named privacy-preserving Distributed Spectral Clustering (ppDSC) is developed. To preserve the edges' privacy, we adopt the randomized response (RR) mechanism to perturb the network edges, which satisfies the strong notion of differential privacy. The ppDSC algorithm is performed on the squared RR-perturbed adjacency matrices to prevent possible cancellation of communities among different layers. To remove the bias incurred by RR and the squared network matrices, we develop a two-step bias-adjustment procedure. Then we perform eigen-decomposition on the debiased matrices, aggregation of the local eigenvectors using an orthogonal Procrustes transformation, and k-means clustering. We provide theoretical analysis on the statistical errors of ppDSC in terms of eigen-vector estimation. In addition, the blessings and curses of network heterogeneity are well-explained by our bounds.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge