Converged Deep Framework Assembling Principled Modules for CS-MRI

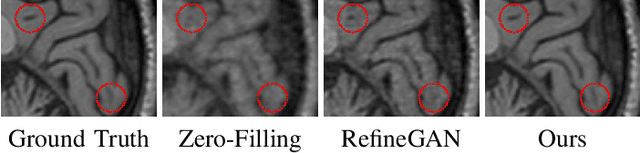
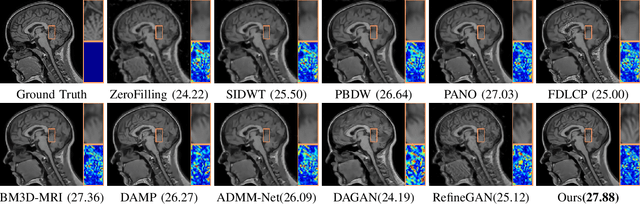
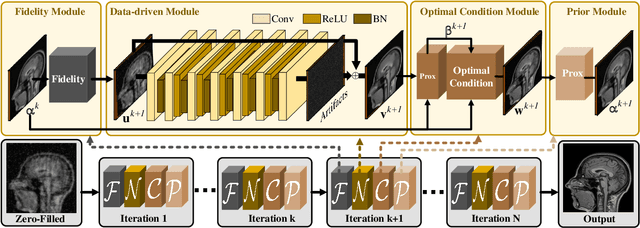
Compressed Sensing Magnetic Resonance Imaging (CS-MRI) significantly accelerates MR data acquisition at a sampling rate much lower than the Nyquist criterion. A major challenge for CS-MRI lies in solving the severely ill-posed inverse problem to reconstruct aliasing-free MR images from the sparse k-space data. Conventional methods typically optimize an energy function, producing reconstruction of high quality, but their iterative numerical solvers unavoidably bring extremely slow processing. Recent data-driven techniques are able to provide fast restoration by either learning direct prediction to final reconstruction or plugging learned modules into the energy optimizer. Nevertheless, these data-driven predictors cannot guarantee the reconstruction following constraints underlying the regularizers of conventional methods so that the reliability of their reconstruction results are questionable. In this paper, we propose a converged deep framework assembling principled modules for CS-MRI that fuses learning strategy with the iterative solver of a conventional reconstruction energy. This framework embeds an optimal condition checking mechanism, fostering \emph{efficient} and \emph{reliable} reconstruction. We also apply the framework to two practical tasks, \emph{i.e.}, parallel imaging and reconstruction with Rician noise. Extensive experiments on both benchmark and manufacturer-testing images demonstrate that the proposed method reliably converges to the optimal solution more efficiently and accurately than the state-of-the-art in various scenarios.

A Theoretically Guaranteed Deep Optimization Framework for Robust Compressive Sensing MRI

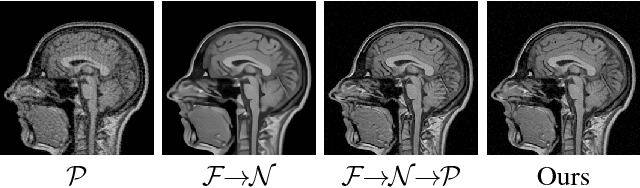
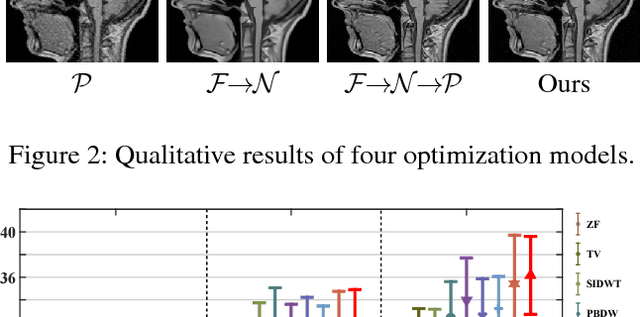
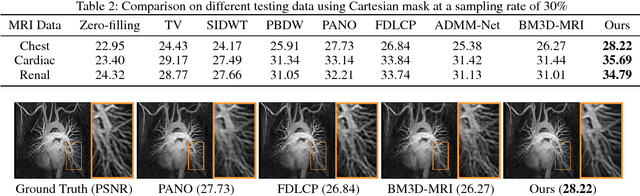
Magnetic Resonance Imaging (MRI) is one of the most dynamic and safe imaging techniques available for clinical applications. However, the rather slow speed of MRI acquisitions limits the patient throughput and potential indi cations. Compressive Sensing (CS) has proven to be an efficient technique for accelerating MRI acquisition. The most widely used CS-MRI model, founded on the premise of reconstructing an image from an incompletely filled k-space, leads to an ill-posed inverse problem. In the past years, lots of efforts have been made to efficiently optimize the CS-MRI model. Inspired by deep learning techniques, some preliminary works have tried to incorporate deep architectures into CS-MRI process. Unfortunately, the convergence issues (due to the experience-based networks) and the robustness (i.e., lack real-world noise modeling) of these deeply trained optimization methods are still missing. In this work, we develop a new paradigm to integrate designed numerical solvers and the data-driven architectures for CS-MRI. By introducing an optimal condition checking mechanism, we can successfully prove the convergence of our established deep CS-MRI optimization scheme. Furthermore, we explicitly formulate the Rician noise distributions within our framework and obtain an extended CS-MRI network to handle the real-world nosies in the MRI process. Extensive experimental results verify that the proposed paradigm outperforms the existing state-of-the-art techniques both in reconstruction accuracy and efficiency as well as robustness to noises in real scene.

On the Convergence of Learning-based Iterative Methods for Nonconvex Inverse Problems

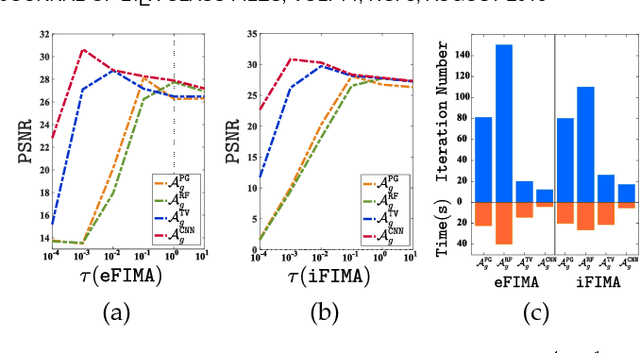
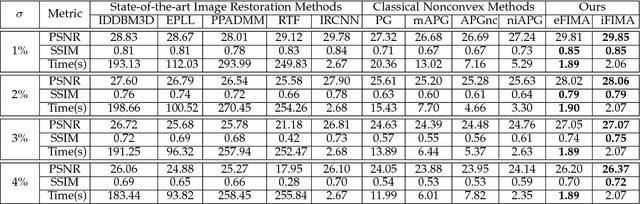
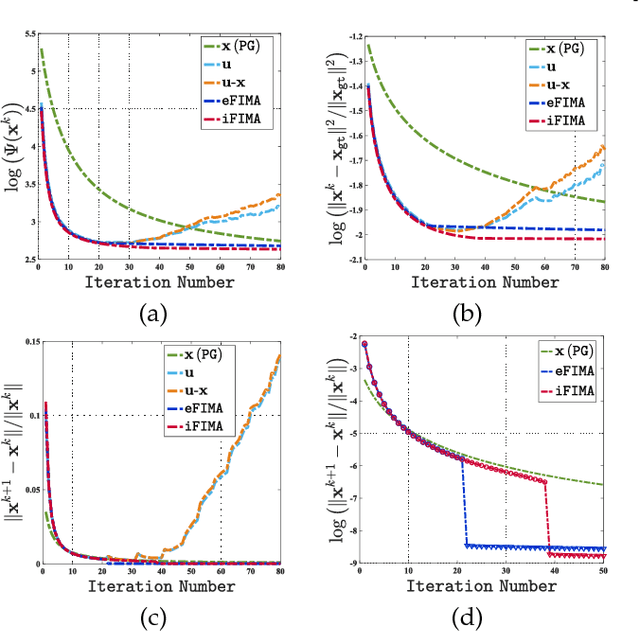
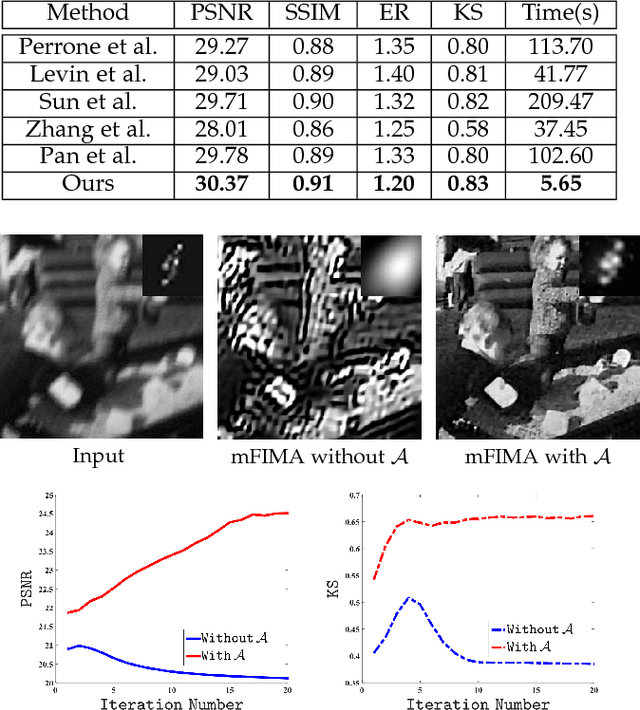
Numerous tasks at the core of statistics, learning and vision areas are specific cases of ill-posed inverse problems. Recently, learning-based (e.g., deep) iterative methods have been empirically shown to be useful for these problems. Nevertheless, integrating learnable structures into iterations is still a laborious process, which can only be guided by intuitions or empirical insights. Moreover, there is a lack of rigorous analysis about the convergence behaviors of these reimplemented iterations, and thus the significance of such methods is a little bit vague. This paper moves beyond these limits and proposes Flexible Iterative Modularization Algorithm (FIMA), a generic and provable paradigm for nonconvex inverse problems. Our theoretical analysis reveals that FIMA allows us to generate globally convergent trajectories for learning-based iterative methods. Meanwhile, the devised scheduling policies on flexible modules should also be beneficial for classical numerical methods in the nonconvex scenario. Extensive experiments on real applications verify the superiority of FIMA.

Learning Collaborative Generation Correction Modules for Blind Image Deblurring and Beyond

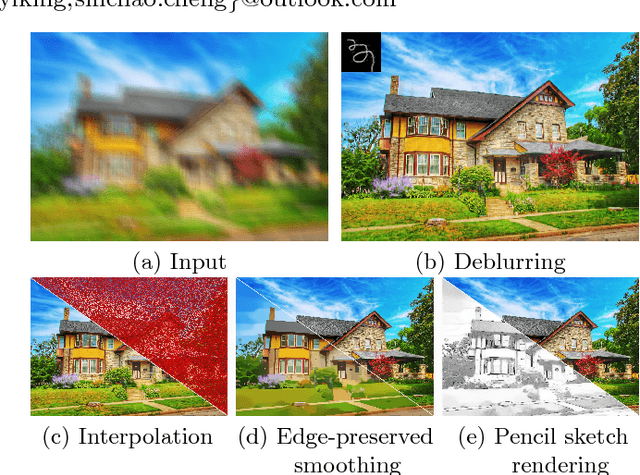
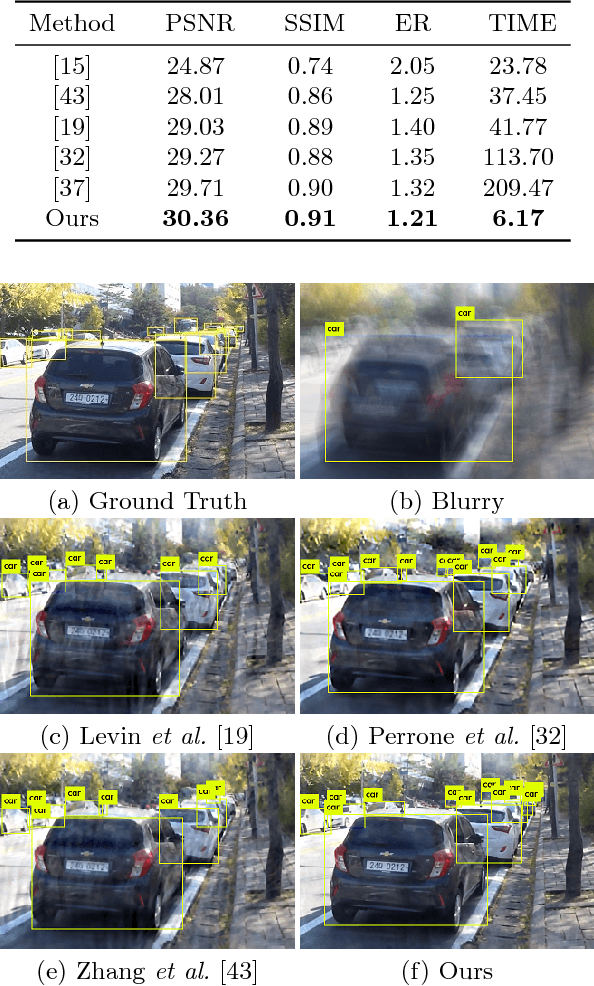
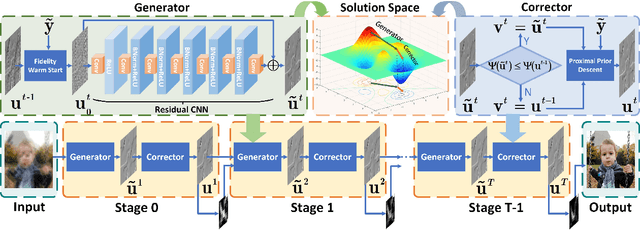
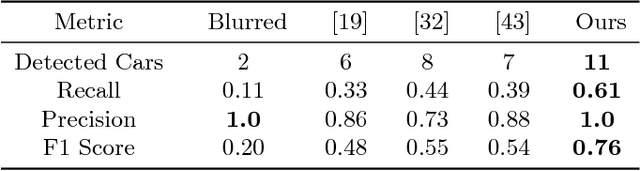
Blind image deblurring plays a very important role in many vision and multimedia applications. Most existing works tend to introduce complex priors to estimate the sharp image structures for blur kernel estimation. However, it has been verified that directly optimizing these models is challenging and easy to fall into degenerate solutions. Although several experience-based heuristic inference strategies, including trained networks and designed iterations, have been developed, it is still hard to obtain theoretically guaranteed accurate solutions. In this work, a collaborative learning framework is established to address the above issues. Specifically, we first design two modules, named Generator and Corrector, to extract the intrinsic image structures from the data-driven and knowledge-based perspectives, respectively. By introducing a collaborative methodology to cascade these modules, we can strictly prove the convergence of our image propagations to a deblurring-related optimal solution. As a nontrivial byproduct, we also apply the proposed method to address other related tasks, such as image interpolation and edge-preserved smoothing. Plenty of experiments demonstrate that our method can outperform the state-of-the-art approaches on both synthetic and real datasets.

Toward Designing Convergent Deep Operator Splitting Methods for Task-specific Nonconvex Optimization

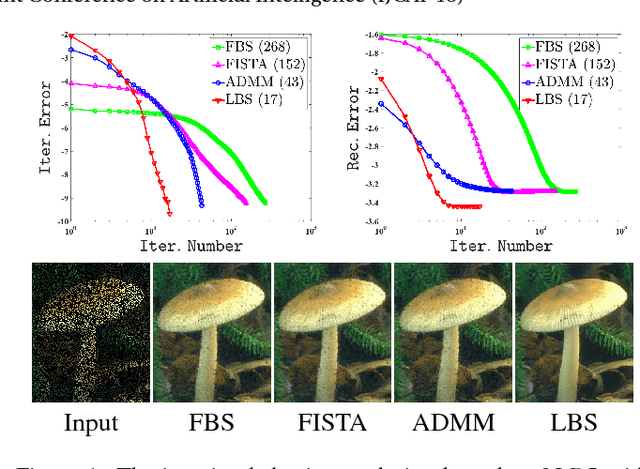
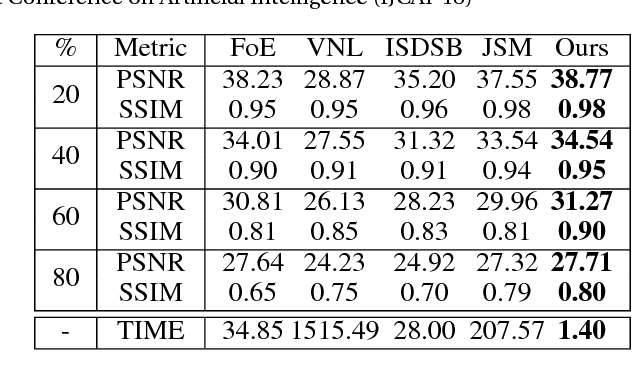
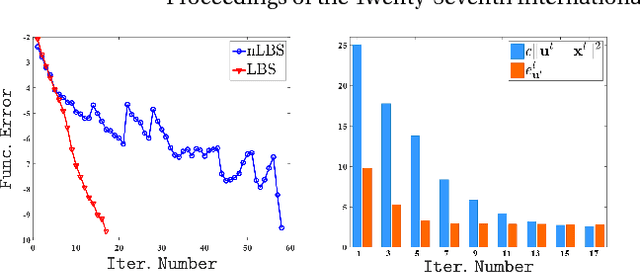
Operator splitting methods have been successfully used in computational sciences, statistics, learning and vision areas to reduce complex problems into a series of simpler subproblems. However, prevalent splitting schemes are mostly established only based on the mathematical properties of some general optimization models. So it is a laborious process and often requires many iterations of ideation and validation to obtain practical and task-specific optimal solutions, especially for nonconvex problems in real-world scenarios. To break through the above limits, we introduce a new algorithmic framework, called Learnable Bregman Splitting (LBS), to perform deep-architecture-based operator splitting for nonconvex optimization based on specific task model. Thanks to the data-dependent (i.e., learnable) nature, our LBS can not only speed up the convergence, but also avoid unwanted trivial solutions for real-world tasks. Though with inexact deep iterations, we can still establish the global convergence and estimate the asymptotic convergence rate of LBS only by enforcing some fairly loose assumptions. Extensive experiments on different applications (e.g., image completion and deblurring) verify our theoretical results and show the superiority of LBS against existing methods.

Proximal Alternating Direction Network: A Globally Converged Deep Unrolling Framework

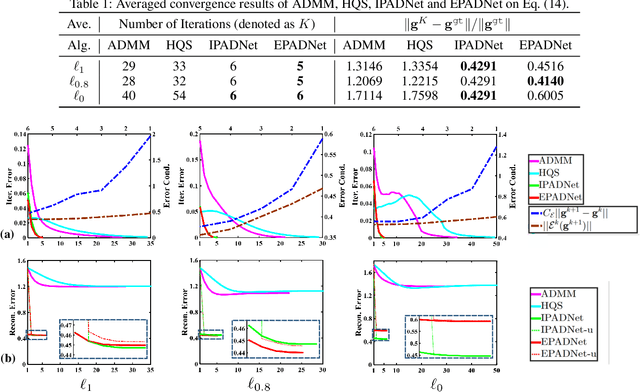
Deep learning models have gained great success in many real-world applications. However, most existing networks are typically designed in heuristic manners, thus lack of rigorous mathematical principles and derivations. Several recent studies build deep structures by unrolling a particular optimization model that involves task information. Unfortunately, due to the dynamic nature of network parameters, their resultant deep propagation networks do \emph{not} possess the nice convergence property as the original optimization scheme does. This paper provides a novel proximal unrolling framework to establish deep models by integrating experimentally verified network architectures and rich cues of the tasks. More importantly, we \emph{prove in theory} that 1) the propagation generated by our unrolled deep model globally converges to a critical-point of a given variational energy, and 2) the proposed framework is still able to learn priors from training data to generate a convergent propagation even when task information is only partially available. Indeed, these theoretical results are the best we can ask for, unless stronger assumptions are enforced. Extensive experiments on various real-world applications verify the theoretical convergence and demonstrate the effectiveness of designed deep models.