On the Convergence of Learning-based Iterative Methods for Nonconvex Inverse Problems
Paper and Code
Aug 16, 2018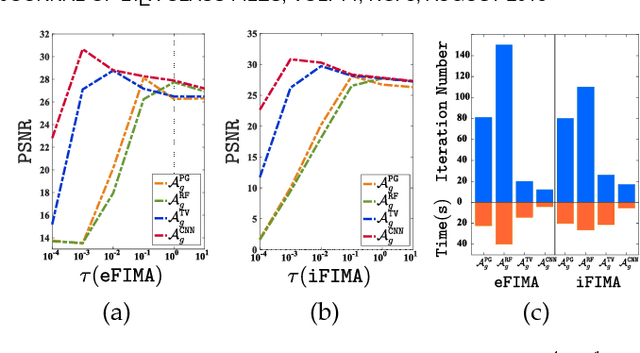
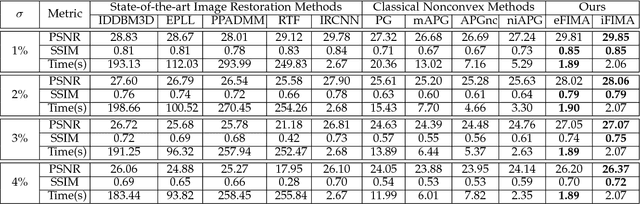
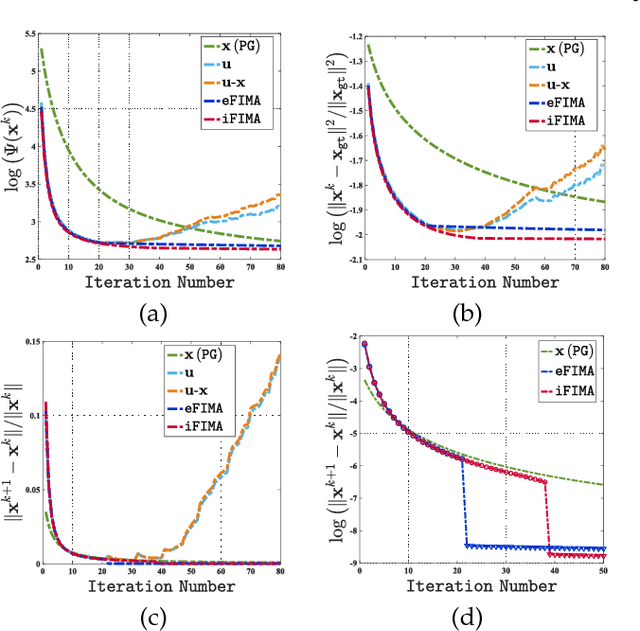
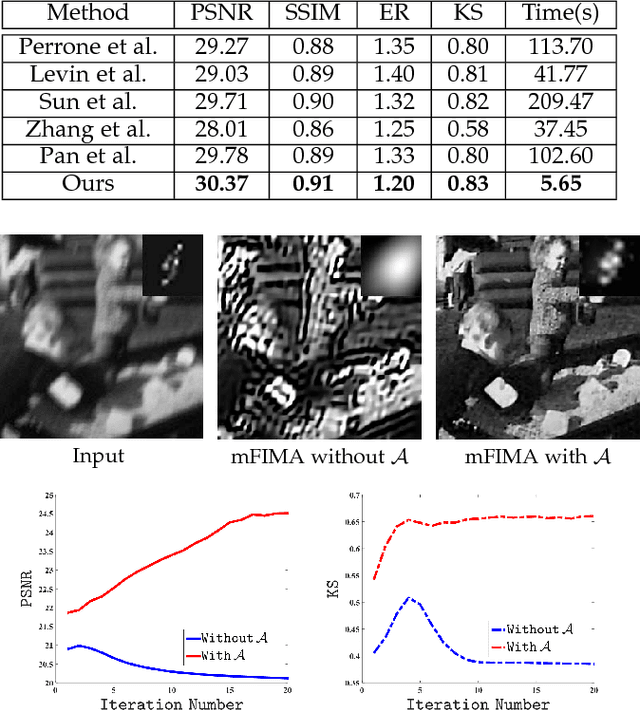
Numerous tasks at the core of statistics, learning and vision areas are specific cases of ill-posed inverse problems. Recently, learning-based (e.g., deep) iterative methods have been empirically shown to be useful for these problems. Nevertheless, integrating learnable structures into iterations is still a laborious process, which can only be guided by intuitions or empirical insights. Moreover, there is a lack of rigorous analysis about the convergence behaviors of these reimplemented iterations, and thus the significance of such methods is a little bit vague. This paper moves beyond these limits and proposes Flexible Iterative Modularization Algorithm (FIMA), a generic and provable paradigm for nonconvex inverse problems. Our theoretical analysis reveals that FIMA allows us to generate globally convergent trajectories for learning-based iterative methods. Meanwhile, the devised scheduling policies on flexible modules should also be beneficial for classical numerical methods in the nonconvex scenario. Extensive experiments on real applications verify the superiority of FIMA.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge