Converged Deep Framework Assembling Principled Modules for CS-MRI
Paper and Code
Oct 29, 2019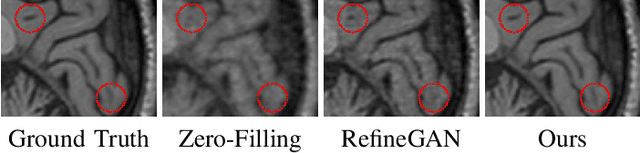
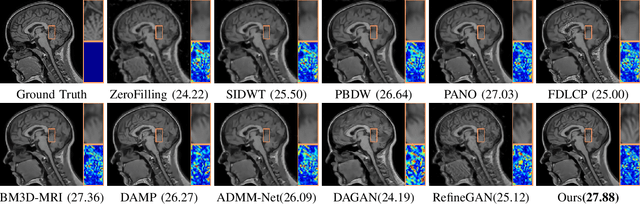

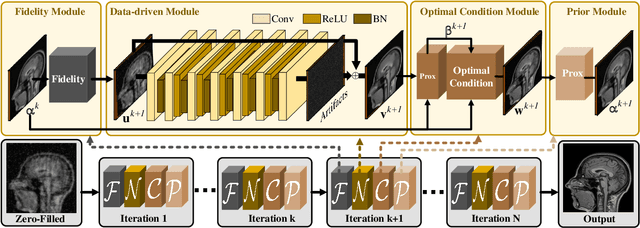
Compressed Sensing Magnetic Resonance Imaging (CS-MRI) significantly accelerates MR data acquisition at a sampling rate much lower than the Nyquist criterion. A major challenge for CS-MRI lies in solving the severely ill-posed inverse problem to reconstruct aliasing-free MR images from the sparse k-space data. Conventional methods typically optimize an energy function, producing reconstruction of high quality, but their iterative numerical solvers unavoidably bring extremely slow processing. Recent data-driven techniques are able to provide fast restoration by either learning direct prediction to final reconstruction or plugging learned modules into the energy optimizer. Nevertheless, these data-driven predictors cannot guarantee the reconstruction following constraints underlying the regularizers of conventional methods so that the reliability of their reconstruction results are questionable. In this paper, we propose a converged deep framework assembling principled modules for CS-MRI that fuses learning strategy with the iterative solver of a conventional reconstruction energy. This framework embeds an optimal condition checking mechanism, fostering \emph{efficient} and \emph{reliable} reconstruction. We also apply the framework to two practical tasks, \emph{i.e.}, parallel imaging and reconstruction with Rician noise. Extensive experiments on both benchmark and manufacturer-testing images demonstrate that the proposed method reliably converges to the optimal solution more efficiently and accurately than the state-of-the-art in various scenarios.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge