Stochastic Normalized Gradient Descent with Momentum for Large Batch Training

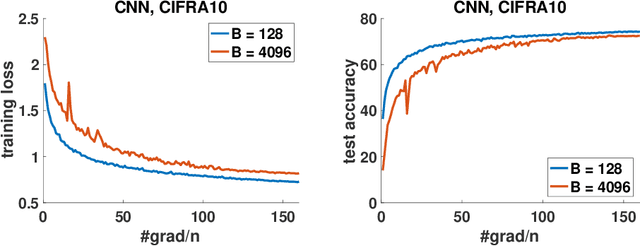
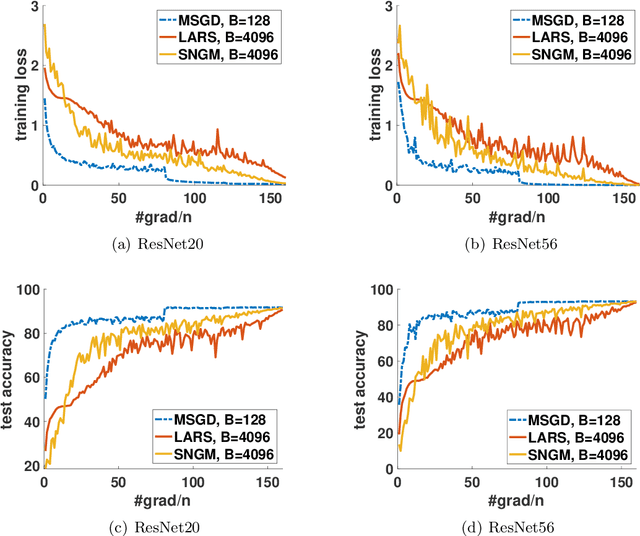
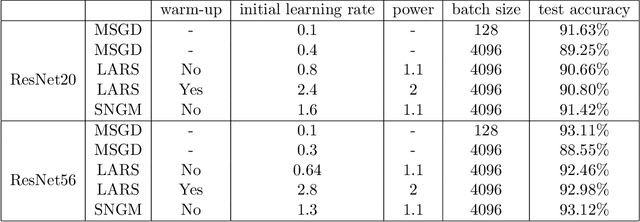
Stochastic gradient descent (SGD) and its variants have been the dominating optimization methods in machine learning. Compared with small batch training, SGD with large batch training can better utilize the computational power of current multi-core systems like GPUs and can reduce the number of communication rounds in distributed training. Hence, SGD with large batch training has attracted more and more attention. However, existing empirical results show that large batch training typically leads to a drop of generalization accuracy. As a result, large batch training has also become a challenging topic. In this paper, we propose a novel method, called stochastic normalized gradient descent with momentum (SNGM), for large batch training. We theoretically prove that compared to momentum SGD (MSGD) which is one of the most widely used variants of SGD, SNGM can adopt a larger batch size to converge to the $\epsilon$-stationary point with the same computation complexity (total number of gradient computation). Empirical results on deep learning also show that SNGM can achieve the state-of-the-art accuracy with a large batch size.

Stagewise Enlargement of Batch Size for SGD-based Learning

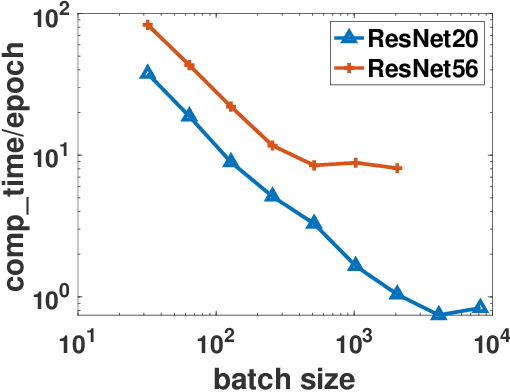
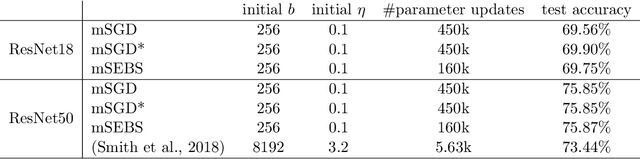
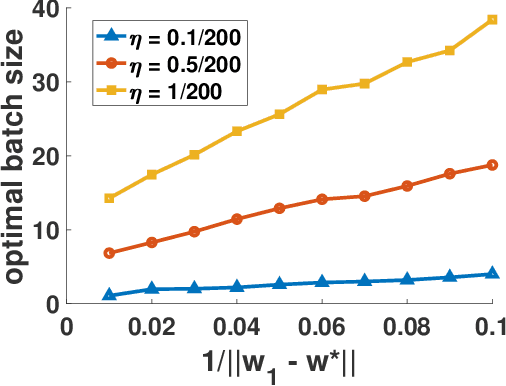
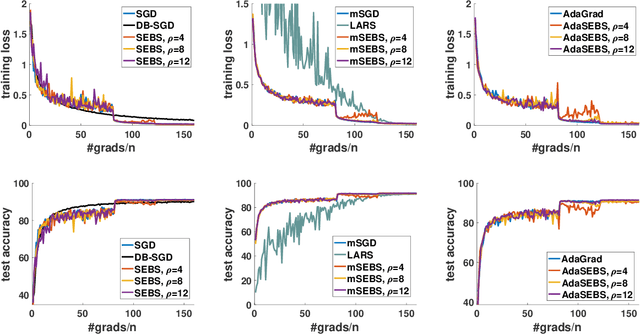
Existing research shows that the batch size can seriously affect the performance of stochastic gradient descent~(SGD) based learning, including training speed and generalization ability. A larger batch size typically results in less parameter updates. In distributed training, a larger batch size also results in less frequent communication. However, a larger batch size can make a generalization gap more easily. Hence, how to set a proper batch size for SGD has recently attracted much attention. Although some methods about setting batch size have been proposed, the batch size problem has still not been well solved. In this paper, we first provide theory to show that a proper batch size is related to the gap between initialization and optimum of the model parameter. Then based on this theory, we propose a novel method, called \underline{s}tagewise \underline{e}nlargement of \underline{b}atch \underline{s}ize~(\mbox{SEBS}), to set proper batch size for SGD. More specifically, \mbox{SEBS} adopts a multi-stage scheme, and enlarges the batch size geometrically by stage. We theoretically prove that, compared to classical stagewise SGD which decreases learning rate by stage, \mbox{SEBS} can reduce the number of parameter updates without increasing generalization error. SEBS is suitable for \mbox{SGD}, momentum \mbox{SGD} and AdaGrad. Empirical results on real data successfully verify the theories of \mbox{SEBS}. Furthermore, empirical results also show that SEBS can outperform other baselines.

ADASS: Adaptive Sample Selection for Training Acceleration

Stochastic gradient decent~(SGD) and its variants, including some accelerated variants, have become popular for training in machine learning. However, in all existing SGD and its variants, the sample size in each iteration~(epoch) of training is the same as the size of the full training set. In this paper, we propose a new method, called \underline{ada}ptive \underline{s}ample \underline{s}election~(ADASS), for training acceleration. During different epoches of training, ADASS only need to visit different training subsets which are adaptively selected from the full training set according to the Lipschitz constants of the loss functions on samples. It means that in ADASS the sample size in each epoch of training can be smaller than the size of the full training set, by discarding some samples. ADASS can be seamlessly integrated with existing optimization methods, such as SGD and momentum SGD, for training acceleration. Theoretical results show that the learning accuracy of ADASS is comparable to that of counterparts with full training set. Furthermore, empirical results on both shallow models and deep models also show that ADASS can accelerate the training process of existing methods without sacrificing accuracy.

Clustered Reinforcement Learning

Exploration strategy design is one of the challenging problems in reinforcement learning~(RL), especially when the environment contains a large state space or sparse rewards. During exploration, the agent tries to discover novel areas or high reward~(quality) areas. In most existing methods, the novelty and quality in the neighboring area of the current state are not well utilized to guide the exploration of the agent. To tackle this problem, we propose a novel RL framework, called \underline{c}lustered \underline{r}einforcement \underline{l}earning~(CRL), for efficient exploration in RL. CRL adopts clustering to divide the collected states into several clusters, based on which a bonus reward reflecting both novelty and quality in the neighboring area~(cluster) of the current state is given to the agent. Experiments on a continuous control task and several \emph{Atari 2600} games show that CRL can outperform other state-of-the-art methods to achieve the best performance in most cases.

On the Convergence of Memory-Based Distributed SGD

Distributed stochastic gradient descent~(DSGD) has been widely used for optimizing large-scale machine learning models, including both convex and non-convex models. With the rapid growth of model size, huge communication cost has been the bottleneck of traditional DSGD. Recently, many communication compression methods have been proposed. Memory-based distributed stochastic gradient descent~(M-DSGD) is one of the efficient methods since each worker communicates a sparse vector in each iteration so that the communication cost is small. Recent works propose the convergence rate of M-DSGD when it adopts vanilla SGD. However, there is still a lack of convergence theory for M-DSGD when it adopts momentum SGD. In this paper, we propose a universal convergence analysis for M-DSGD by introducing \emph{transformation equation}. The transformation equation describes the relation between traditional DSGD and M-DSGD so that we can transform M-DSGD to its corresponding DSGD. Hence we get the convergence rate of M-DSGD with momentum for both convex and non-convex problems. Furthermore, we combine M-DSGD and stagewise learning that the learning rate of M-DSGD in each stage is a constant and is decreased by stage, instead of iteration. Using the transformation equation, we propose the convergence rate of stagewise M-DSGD which bridges the gap between theory and practice.

Global Momentum Compression for Sparse Communication in Distributed SGD

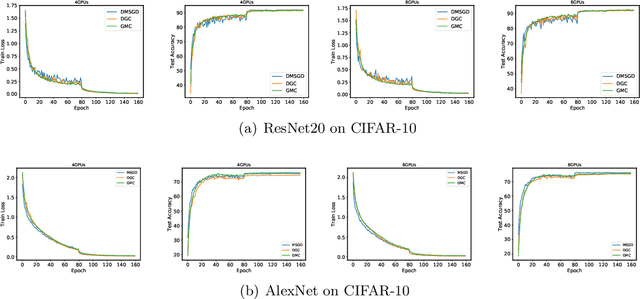
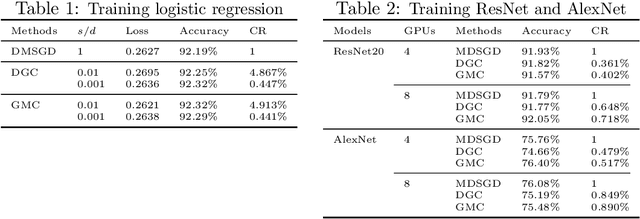
With the rapid growth of data, distributed stochastic gradient descent~(DSGD) has been widely used for solving large-scale machine learning problems. Due to the latency and limited bandwidth of network, communication has become the bottleneck of DSGD when we need to train large scale models, like deep neural networks. Communication compression with sparsified gradient, abbreviated as \emph{sparse communication}, has been widely used for reducing communication cost in DSGD. Recently, there has appeared one method, called deep gradient compression~(DGC), to combine memory gradient and momentum SGD for sparse communication. DGC has achieved promising performance in practise. However, the theory about the convergence of DGC is lack. In this paper, we propose a novel method, called \emph{\underline{g}}lobal \emph{\underline{m}}omentum \emph{\underline{c}}ompression~(GMC), for sparse communication in DSGD. GMC also combines memory gradient and momentum SGD. But different from DGC which adopts local momentum, GMC adopts global momentum. We theoretically prove the convergence rate of GMC for both convex and non-convex problems. To the best of our knowledge, this is the first work that proves the convergence of distributed momentum SGD~(DMSGD) with sparse communication and memory gradient. Empirical results show that, compared with the DMSGD counterpart without sparse communication, GMC can reduce the communication cost by approximately 100 fold without loss of generalization accuracy. GMC can also achieve comparable~(sometimes better) performance compared with DGC, with extra theoretical guarantee.

Quantized Epoch-SGD for Communication-Efficient Distributed Learning

Due to its efficiency and ease to implement, stochastic gradient descent (SGD) has been widely used in machine learning. In particular, SGD is one of the most popular optimization methods for distributed learning. Recently, quantized SGD (QSGD), which adopts quantization to reduce the communication cost in SGD-based distributed learning, has attracted much attention. Although several QSGD methods have been proposed, some of them are heuristic without theoretical guarantee, and others have high quantization variance which makes the convergence become slow. In this paper, we propose a new method, called Quantized Epoch-SGD (QESGD), for communication-efficient distributed learning. QESGD compresses (quantizes) the parameter with variance reduction, so that it can get almost the same performance as that of SGD with less communication cost. QESGD is implemented on the Parameter Server framework, and empirical results on distributed deep learning show that QESGD can outperform other state-of-the-art quantization methods to achieve the best performance.

Proximal SCOPE for Distributed Sparse Learning: Better Data Partition Implies Faster Convergence Rate

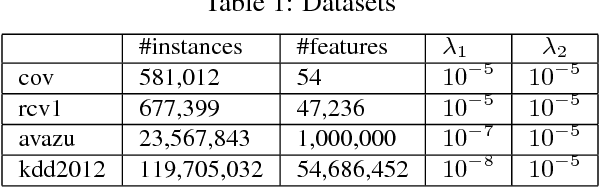
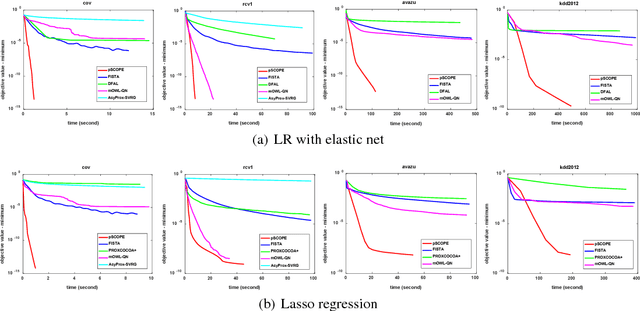
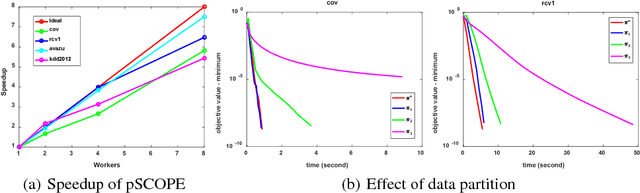
Distributed sparse learning with a cluster of multiple machines has attracted much attention in machine learning, especially for large-scale applications with high-dimensional data. One popular way to implement sparse learning is to use $L_1$ regularization. In this paper, we propose a novel method, called proximal \mbox{SCOPE}~(\mbox{pSCOPE}), for distributed sparse learning with $L_1$ regularization. pSCOPE is based on a \underline{c}ooperative \underline{a}utonomous \underline{l}ocal \underline{l}earning~(\mbox{CALL}) framework. In the \mbox{CALL} framework of \mbox{pSCOPE}, we find that the data partition affects the convergence of the learning procedure, and subsequently we define a metric to measure the goodness of a data partition. Based on the defined metric, we theoretically prove that pSCOPE is convergent with a linear convergence rate if the data partition is good enough. We also prove that better data partition implies faster convergence rate. Furthermore, pSCOPE is also communication efficient. Experimental results on real data sets show that pSCOPE can outperform other state-of-the-art distributed methods for sparse learning.

Feature-Distributed SVRG for High-Dimensional Linear Classification

Linear classification has been widely used in many high-dimensional applications like text classification. To perform linear classification for large-scale tasks, we often need to design distributed learning methods on a cluster of multiple machines. In this paper, we propose a new distributed learning method, called feature-distributed stochastic variance reduced gradient (FD-SVRG) for high-dimensional linear classification. Unlike most existing distributed learning methods which are instance-distributed, FD-SVRG is feature-distributed. FD-SVRG has lower communication cost than other instance-distributed methods when the data dimensionality is larger than the number of data instances. Experimental results on real data demonstrate that FD-SVRG can outperform other state-of-the-art distributed methods for high-dimensional linear classification in terms of both communication cost and wall-clock time, when the dimensionality is larger than the number of instances in training data.

Lock-Free Optimization for Non-Convex Problems

Stochastic gradient descent~(SGD) and its variants have attracted much attention in machine learning due to their efficiency and effectiveness for optimization. To handle large-scale problems, researchers have recently proposed several lock-free strategy based parallel SGD~(LF-PSGD) methods for multi-core systems. However, existing works have only proved the convergence of these LF-PSGD methods for convex problems. To the best of our knowledge, no work has proved the convergence of the LF-PSGD methods for non-convex problems. In this paper, we provide the theoretical proof about the convergence of two representative LF-PSGD methods, Hogwild! and AsySVRG, for non-convex problems. Empirical results also show that both Hogwild! and AsySVRG are convergent on non-convex problems, which successfully verifies our theoretical results.