Proximal SCOPE for Distributed Sparse Learning: Better Data Partition Implies Faster Convergence Rate
Paper and Code
Oct 26, 2018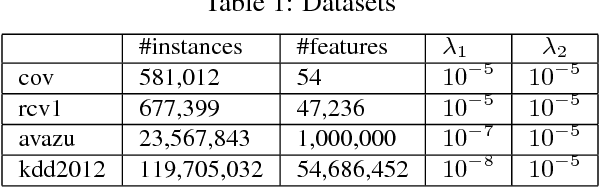
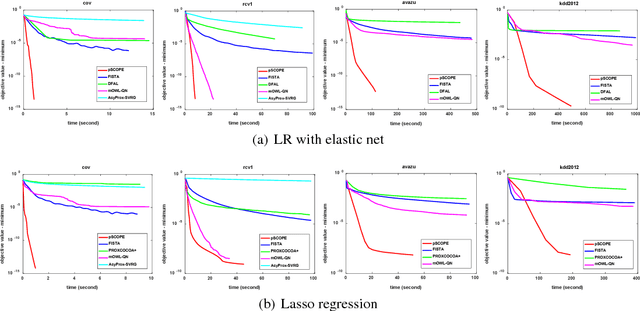
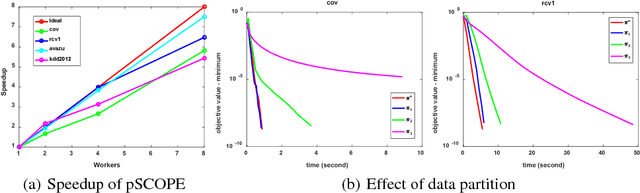
Distributed sparse learning with a cluster of multiple machines has attracted much attention in machine learning, especially for large-scale applications with high-dimensional data. One popular way to implement sparse learning is to use $L_1$ regularization. In this paper, we propose a novel method, called proximal \mbox{SCOPE}~(\mbox{pSCOPE}), for distributed sparse learning with $L_1$ regularization. pSCOPE is based on a \underline{c}ooperative \underline{a}utonomous \underline{l}ocal \underline{l}earning~(\mbox{CALL}) framework. In the \mbox{CALL} framework of \mbox{pSCOPE}, we find that the data partition affects the convergence of the learning procedure, and subsequently we define a metric to measure the goodness of a data partition. Based on the defined metric, we theoretically prove that pSCOPE is convergent with a linear convergence rate if the data partition is good enough. We also prove that better data partition implies faster convergence rate. Furthermore, pSCOPE is also communication efficient. Experimental results on real data sets show that pSCOPE can outperform other state-of-the-art distributed methods for sparse learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge