Breaking the Barrier: Utilizing Large Language Models for Industrial Recommendation Systems through an Inferential Knowledge Graph

Recommendation systems are widely used in e-commerce websites and online platforms to address information overload. However, existing systems primarily rely on historical data and user feedback, making it difficult to capture user intent transitions. Recently, Knowledge Base (KB)-based models are proposed to incorporate expert knowledge, but it struggle to adapt to new items and the evolving e-commerce environment. To address these challenges, we propose a novel Large Language Model based Complementary Knowledge Enhanced Recommendation System (LLM-KERec). It introduces an entity extractor that extracts unified concept terms from item and user information. To provide cost-effective and reliable prior knowledge, entity pairs are generated based on entity popularity and specific strategies. The large language model determines complementary relationships in each entity pair, constructing a complementary knowledge graph. Furthermore, a new complementary recall module and an Entity-Entity-Item (E-E-I) weight decision model refine the scoring of the ranking model using real complementary exposure-click samples. Extensive experiments conducted on three industry datasets demonstrate the significant performance improvement of our model compared to existing approaches. Additionally, detailed analysis shows that LLM-KERec enhances users' enthusiasm for consumption by recommending complementary items. In summary, LLM-KERec addresses the limitations of traditional recommendation systems by incorporating complementary knowledge and utilizing a large language model to capture user intent transitions, adapt to new items, and enhance recommendation efficiency in the evolving e-commerce landscape.

Proximal SCOPE for Distributed Sparse Learning: Better Data Partition Implies Faster Convergence Rate

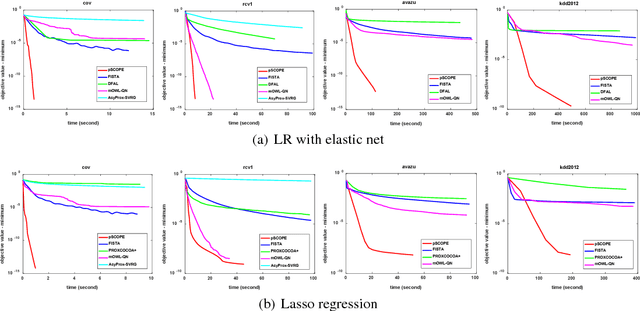
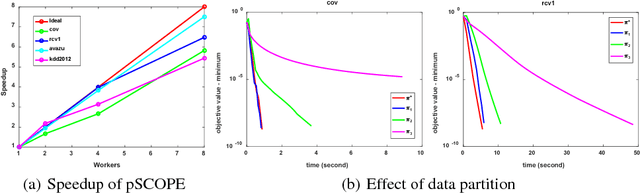
Distributed sparse learning with a cluster of multiple machines has attracted much attention in machine learning, especially for large-scale applications with high-dimensional data. One popular way to implement sparse learning is to use $L_1$ regularization. In this paper, we propose a novel method, called proximal \mbox{SCOPE}~(\mbox{pSCOPE}), for distributed sparse learning with $L_1$ regularization. pSCOPE is based on a \underline{c}ooperative \underline{a}utonomous \underline{l}ocal \underline{l}earning~(\mbox{CALL}) framework. In the \mbox{CALL} framework of \mbox{pSCOPE}, we find that the data partition affects the convergence of the learning procedure, and subsequently we define a metric to measure the goodness of a data partition. Based on the defined metric, we theoretically prove that pSCOPE is convergent with a linear convergence rate if the data partition is good enough. We also prove that better data partition implies faster convergence rate. Furthermore, pSCOPE is also communication efficient. Experimental results on real data sets show that pSCOPE can outperform other state-of-the-art distributed methods for sparse learning.

Feature-Distributed SVRG for High-Dimensional Linear Classification

Linear classification has been widely used in many high-dimensional applications like text classification. To perform linear classification for large-scale tasks, we often need to design distributed learning methods on a cluster of multiple machines. In this paper, we propose a new distributed learning method, called feature-distributed stochastic variance reduced gradient (FD-SVRG) for high-dimensional linear classification. Unlike most existing distributed learning methods which are instance-distributed, FD-SVRG is feature-distributed. FD-SVRG has lower communication cost than other instance-distributed methods when the data dimensionality is larger than the number of data instances. Experimental results on real data demonstrate that FD-SVRG can outperform other state-of-the-art distributed methods for high-dimensional linear classification in terms of both communication cost and wall-clock time, when the dimensionality is larger than the number of instances in training data.

Lock-Free Optimization for Non-Convex Problems

Stochastic gradient descent~(SGD) and its variants have attracted much attention in machine learning due to their efficiency and effectiveness for optimization. To handle large-scale problems, researchers have recently proposed several lock-free strategy based parallel SGD~(LF-PSGD) methods for multi-core systems. However, existing works have only proved the convergence of these LF-PSGD methods for convex problems. To the best of our knowledge, no work has proved the convergence of the LF-PSGD methods for non-convex problems. In this paper, we provide the theoretical proof about the convergence of two representative LF-PSGD methods, Hogwild! and AsySVRG, for non-convex problems. Empirical results also show that both Hogwild! and AsySVRG are convergent on non-convex problems, which successfully verifies our theoretical results.