Stochastic Normalized Gradient Descent with Momentum for Large Batch Training

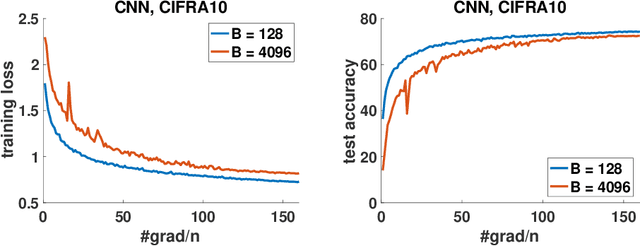
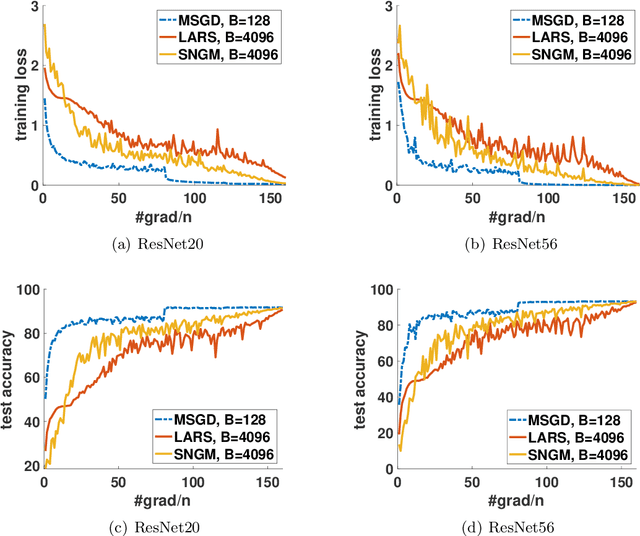
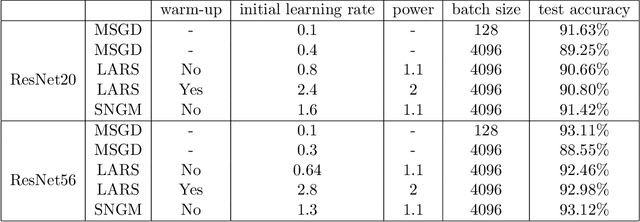
Stochastic gradient descent (SGD) and its variants have been the dominating optimization methods in machine learning. Compared with small batch training, SGD with large batch training can better utilize the computational power of current multi-core systems like GPUs and can reduce the number of communication rounds in distributed training. Hence, SGD with large batch training has attracted more and more attention. However, existing empirical results show that large batch training typically leads to a drop of generalization accuracy. As a result, large batch training has also become a challenging topic. In this paper, we propose a novel method, called stochastic normalized gradient descent with momentum (SNGM), for large batch training. We theoretically prove that compared to momentum SGD (MSGD) which is one of the most widely used variants of SGD, SNGM can adopt a larger batch size to converge to the $\epsilon$-stationary point with the same computation complexity (total number of gradient computation). Empirical results on deep learning also show that SNGM can achieve the state-of-the-art accuracy with a large batch size.