Stochastic Normalized Gradient Descent with Momentum for Large Batch Training

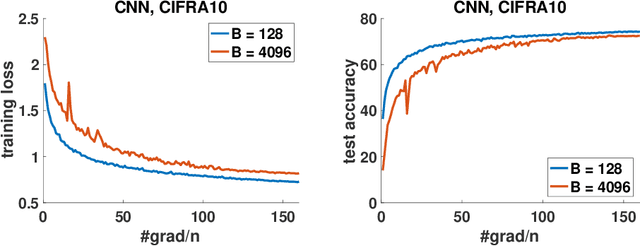
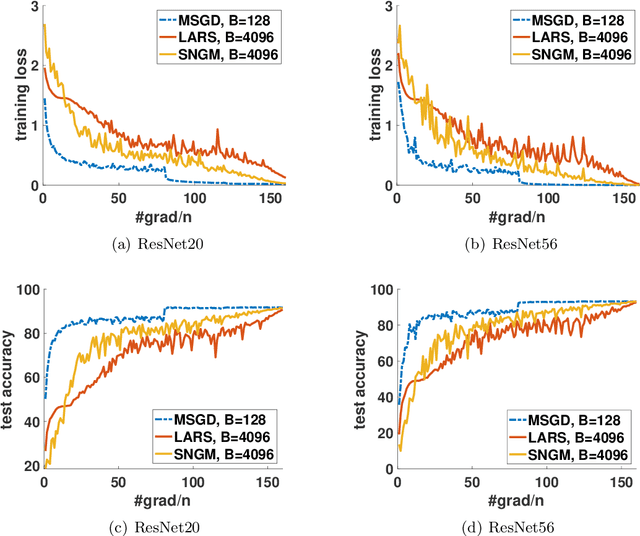
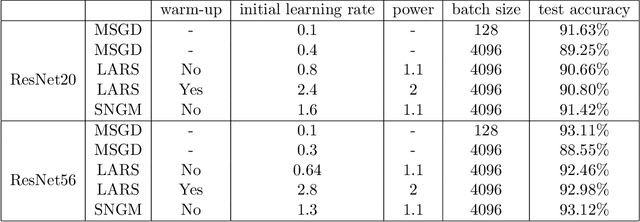
Stochastic gradient descent (SGD) and its variants have been the dominating optimization methods in machine learning. Compared with small batch training, SGD with large batch training can better utilize the computational power of current multi-core systems like GPUs and can reduce the number of communication rounds in distributed training. Hence, SGD with large batch training has attracted more and more attention. However, existing empirical results show that large batch training typically leads to a drop of generalization accuracy. As a result, large batch training has also become a challenging topic. In this paper, we propose a novel method, called stochastic normalized gradient descent with momentum (SNGM), for large batch training. We theoretically prove that compared to momentum SGD (MSGD) which is one of the most widely used variants of SGD, SNGM can adopt a larger batch size to converge to the $\epsilon$-stationary point with the same computation complexity (total number of gradient computation). Empirical results on deep learning also show that SNGM can achieve the state-of-the-art accuracy with a large batch size.

Stagewise Enlargement of Batch Size for SGD-based Learning

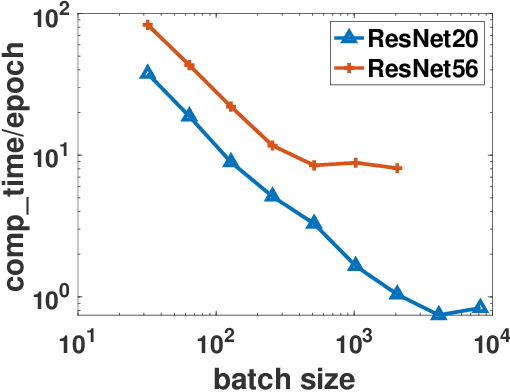
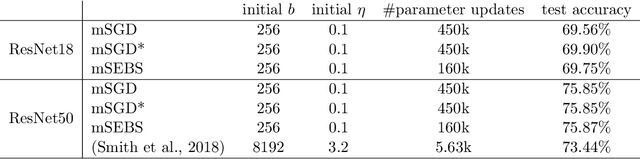
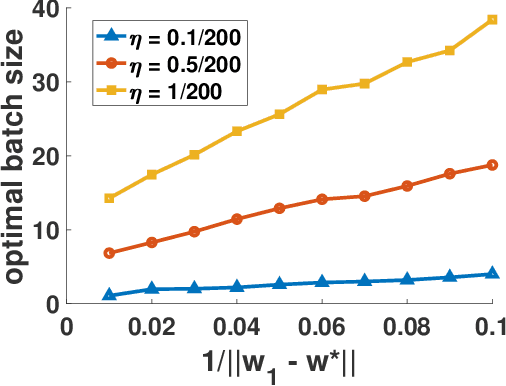
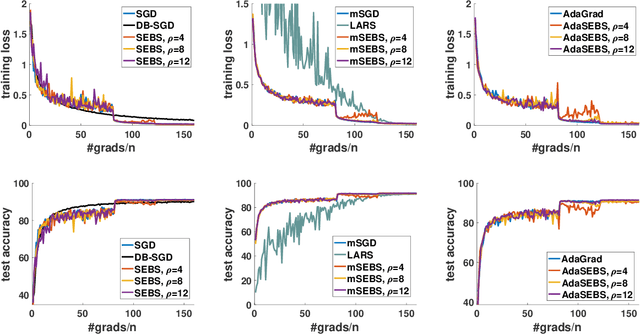
Existing research shows that the batch size can seriously affect the performance of stochastic gradient descent~(SGD) based learning, including training speed and generalization ability. A larger batch size typically results in less parameter updates. In distributed training, a larger batch size also results in less frequent communication. However, a larger batch size can make a generalization gap more easily. Hence, how to set a proper batch size for SGD has recently attracted much attention. Although some methods about setting batch size have been proposed, the batch size problem has still not been well solved. In this paper, we first provide theory to show that a proper batch size is related to the gap between initialization and optimum of the model parameter. Then based on this theory, we propose a novel method, called \underline{s}tagewise \underline{e}nlargement of \underline{b}atch \underline{s}ize~(\mbox{SEBS}), to set proper batch size for SGD. More specifically, \mbox{SEBS} adopts a multi-stage scheme, and enlarges the batch size geometrically by stage. We theoretically prove that, compared to classical stagewise SGD which decreases learning rate by stage, \mbox{SEBS} can reduce the number of parameter updates without increasing generalization error. SEBS is suitable for \mbox{SGD}, momentum \mbox{SGD} and AdaGrad. Empirical results on real data successfully verify the theories of \mbox{SEBS}. Furthermore, empirical results also show that SEBS can outperform other baselines.

Global Momentum Compression for Sparse Communication in Distributed SGD

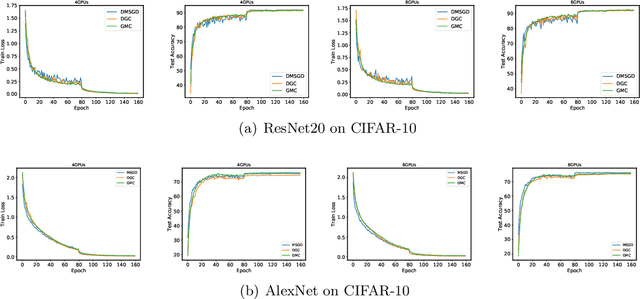
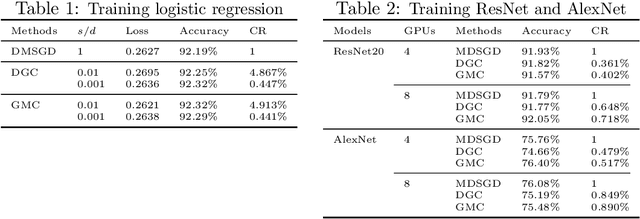
With the rapid growth of data, distributed stochastic gradient descent~(DSGD) has been widely used for solving large-scale machine learning problems. Due to the latency and limited bandwidth of network, communication has become the bottleneck of DSGD when we need to train large scale models, like deep neural networks. Communication compression with sparsified gradient, abbreviated as \emph{sparse communication}, has been widely used for reducing communication cost in DSGD. Recently, there has appeared one method, called deep gradient compression~(DGC), to combine memory gradient and momentum SGD for sparse communication. DGC has achieved promising performance in practise. However, the theory about the convergence of DGC is lack. In this paper, we propose a novel method, called \emph{\underline{g}}lobal \emph{\underline{m}}omentum \emph{\underline{c}}ompression~(GMC), for sparse communication in DSGD. GMC also combines memory gradient and momentum SGD. But different from DGC which adopts local momentum, GMC adopts global momentum. We theoretically prove the convergence rate of GMC for both convex and non-convex problems. To the best of our knowledge, this is the first work that proves the convergence of distributed momentum SGD~(DMSGD) with sparse communication and memory gradient. Empirical results show that, compared with the DMSGD counterpart without sparse communication, GMC can reduce the communication cost by approximately 100 fold without loss of generalization accuracy. GMC can also achieve comparable~(sometimes better) performance compared with DGC, with extra theoretical guarantee.