Experimental Realization of Convolution Processing in Photonic Synthetic Frequency Dimensions

Convolution is an essential operation in signal and image processing and consumes most of the computing power in convolutional neural networks. Photonic convolution has the promise of addressing computational bottlenecks and outperforming electronic implementations. Performing photonic convolution in the synthetic frequency dimension, which harnesses the dynamics of light in the spectral degrees of freedom for photons, can lead to highly compact devices. Here we experimentally realize convolution operations in the synthetic frequency dimension. Using a modulated ring resonator, we synthesize arbitrary convolution kernels using a pre-determined modulation waveform with high accuracy. We demonstrate the convolution computation between input frequency combs and synthesized kernels. We also introduce the idea of an additive offset to broaden the kinds of kernels that can be implemented experimentally when the modulation strength is limited. Our work demonstrate the use of synthetic frequency dimension to efficiently encode data and implement computation tasks, leading to a compact and scalable photonic computation architecture.

Scalable and self-correcting photonic computation using balanced photonic binary tree cascades

Programmable unitary photonic networks that interfere hundreds of modes are emerging as a key technology in energy-efficient sensing, machine learning, cryptography, and linear optical quantum computing applications. In this work, we establish a theoretical framework to quantify error tolerance and scalability in a more general class of "binary tree cascade'' programmable photonic networks that accept up to tens of thousands of discrete input modes $N$. To justify this scalability claim, we derive error tolerance and configuration time that scale with $\log_2 N$ for balanced trees versus $N$ in unbalanced trees, despite the same number of total components. Specifically, we use second-order perturbation theory to compute phase sensitivity in each waveguide of balanced and unbalanced networks, and we compute the statistics of the sensitivity given random input vectors. We also evaluate such networks after they self-correct, or self-configure, themselves for errors in the circuit due to fabrication error and environmental drift. Our findings have important implications for scaling photonic circuits to much larger circuit sizes; this scaling is particularly critical for applications such as principal component analysis and fast Fourier transforms, which are important algorithms for machine learning and signal processing.

Experimentally realized in situ backpropagation for deep learning in nanophotonic neural networks

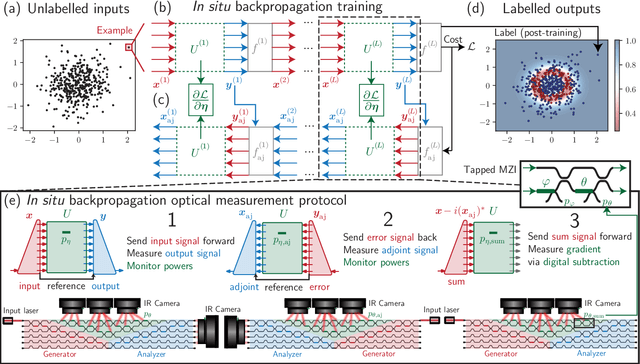
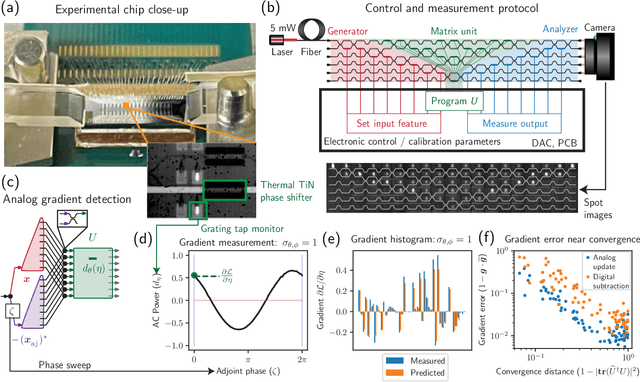
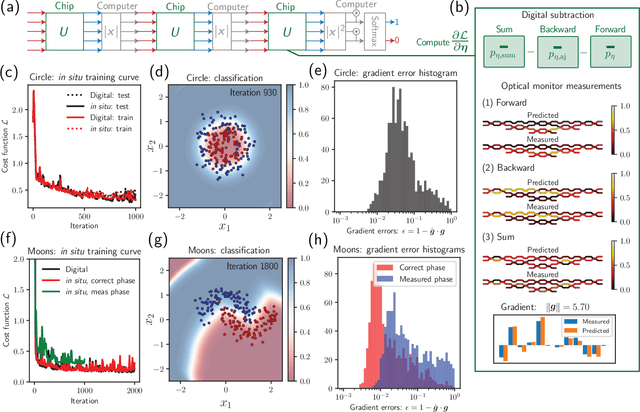
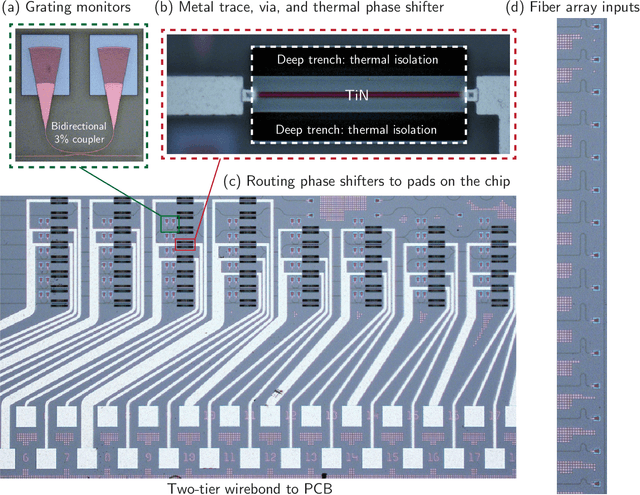
Neural networks are widely deployed models across many scientific disciplines and commercial endeavors ranging from edge computing and sensing to large-scale signal processing in data centers. The most efficient and well-entrenched method to train such networks is backpropagation, or reverse-mode automatic differentiation. To counter an exponentially increasing energy budget in the artificial intelligence sector, there has been recent interest in analog implementations of neural networks, specifically nanophotonic neural networks for which no analog backpropagation demonstration exists. We design mass-manufacturable silicon photonic neural networks that alternately cascade our custom designed "photonic mesh" accelerator with digitally implemented nonlinearities. These reconfigurable photonic meshes program computationally intensive arbitrary matrix multiplication by setting physical voltages that tune the interference of optically encoded input data propagating through integrated Mach-Zehnder interferometer networks. Here, using our packaged photonic chip, we demonstrate in situ backpropagation for the first time to solve classification tasks and evaluate a new protocol to keep the entire gradient measurement and update of physical device voltages in the analog domain, improving on past theoretical proposals. Our method is made possible by introducing three changes to typical photonic meshes: (1) measurements at optical "grating tap" monitors, (2) bidirectional optical signal propagation automated by fiber switch, and (3) universal generation and readout of optical amplitude and phase. After training, our classification achieves accuracies similar to digital equivalents even in presence of systematic error. Our findings suggest a new training paradigm for photonics-accelerated artificial intelligence based entirely on a physical analog of the popular backpropagation technique.

Parallel fault-tolerant programming of an arbitrary feedforward photonic network

Reconfigurable photonic mesh networks of tunable beamsplitter nodes can linearly transform $N$-dimensional vectors representing input modal amplitudes of light for applications such as energy-efficient machine learning hardware, quantum information processing, and mode demultiplexing. Such photonic meshes are typically programmed and/or calibrated by tuning or characterizing each beam splitter one-by-one, which can be time-consuming and can limit scaling to larger meshes. Here we introduce a graph-topological approach that defines the general class of feedforward networks commonly used in such applications and identifies columns of non-interacting nodes that can be adjusted simultaneously. By virtue of this approach, we can calculate the necessary input vectors to program entire columns of nodes in parallel by simultaneously nullifying the power in one output of each node via optoelectronic feedback onto adjustable phase shifters or couplers. This parallel nullification approach is fault-tolerant to fabrication errors, requiring no prior knowledge or calibration of the node parameters, and can reduce the programming time by a factor of order $N$ to being proportional to the optical depth (or number of node columns in the device). As a demonstration, we simulate our programming protocol on a feedforward optical neural network model trained to classify handwritten digit images from the MNIST dataset with up to 98% validation accuracy.

Wave Physics as an Analog Recurrent Neural Network

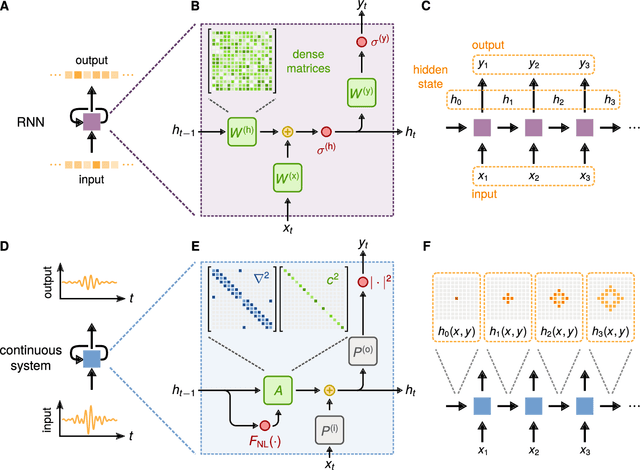
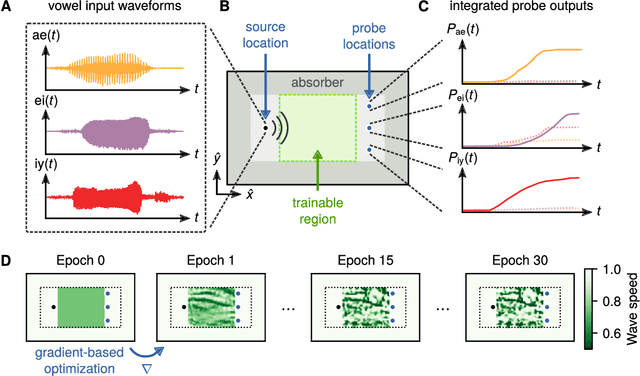
Analog machine learning hardware platforms promise to be faster and more energy-efficient than their digital counterparts. Wave physics, as found in acoustics and optics, is a natural candidate for building analog processors for time-varying signals. Here we identify a mapping between the dynamics of wave physics, and the computation in recurrent neural networks. This mapping indicates that physical wave systems can be trained to learn complex features in temporal data, using standard training techniques for neural networks. As a demonstration, we show that an inversely-designed inhomogeneous medium can perform vowel classification on raw audio data by simple propagation of waves through such a medium, achieving performance that is comparable to a standard digital implementation of a recurrent neural network. These findings pave the way for a new class of analog machine learning platforms, capable of fast and efficient processing of information in its native domain.

Direct Object Recognition Without Line-of-Sight Using Optical Coherence

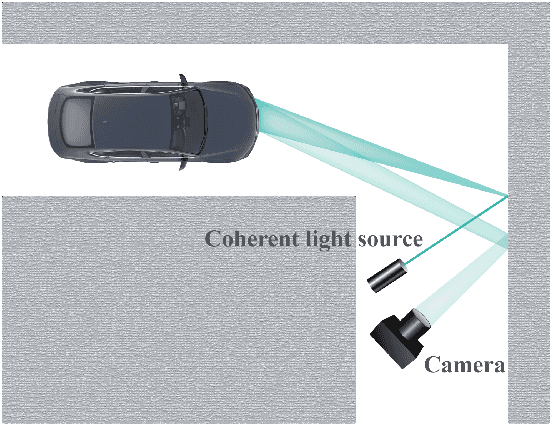
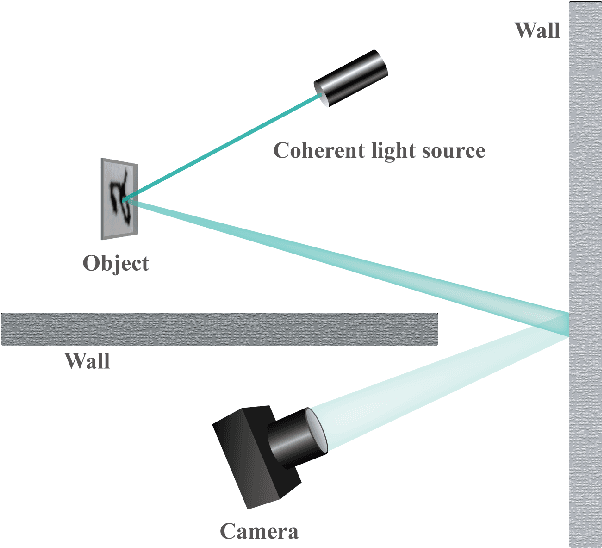
Visual object recognition under situations in which the direct line-of-sight is blocked, such as when it is occluded around the corner, is of practical importance in a wide range of applications. With coherent illumination, the light scattered from diffusive walls forms speckle patterns that contain information of the hidden object. It is possible to realize non-line-of-sight (NLOS) recognition with these speckle patterns. We introduce a novel approach based on speckle pattern recognition with deep neural network, which is simpler and more robust than other NLOS recognition methods. Simulations and experiments are performed to verify the feasibility and performance of this approach.

Reprogrammable Electro-Optic Nonlinear Activation Functions for Optical Neural Networks

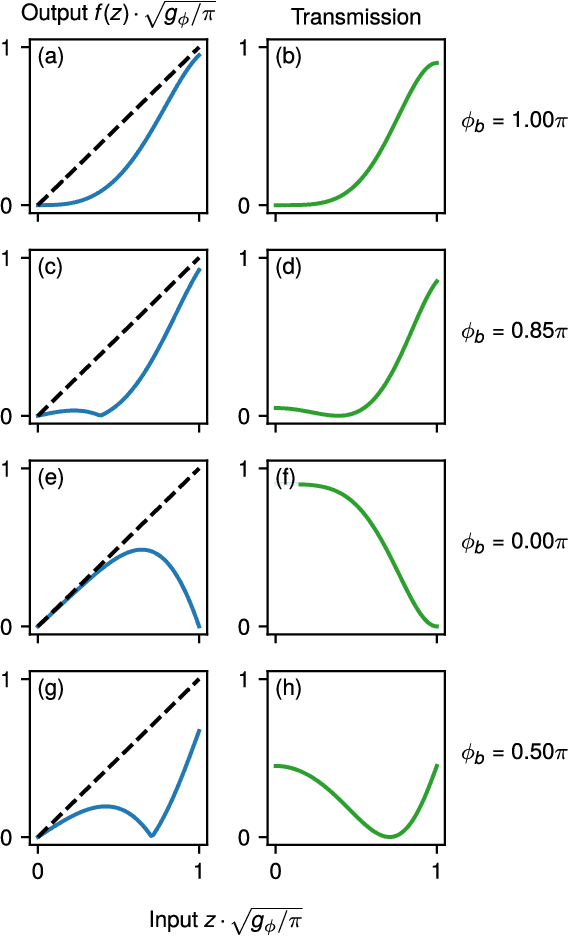
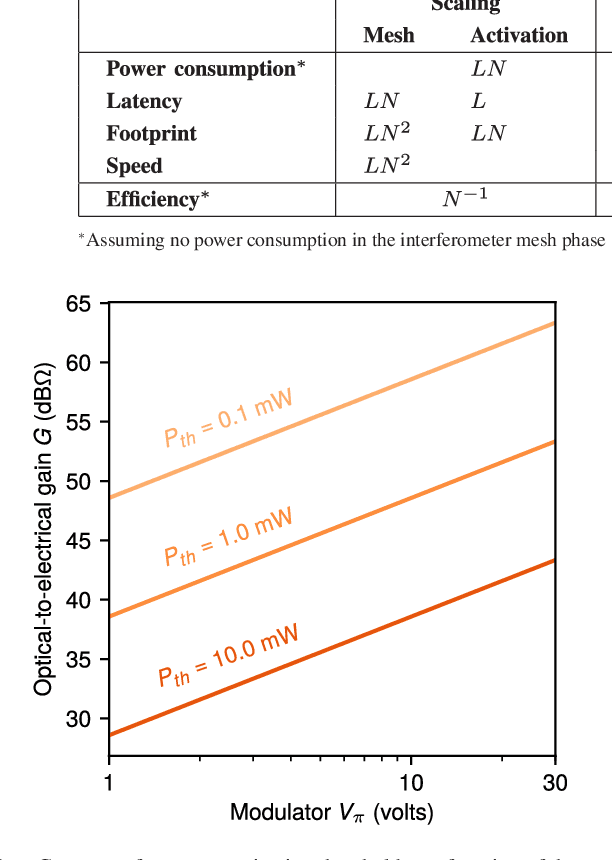
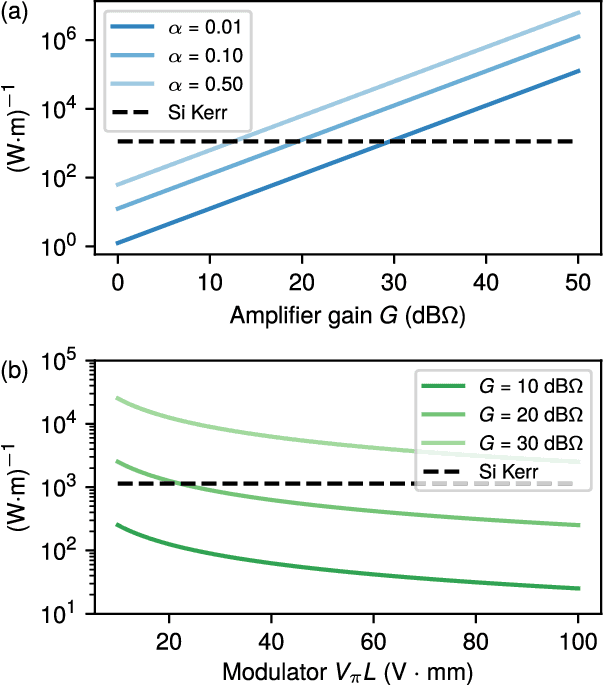
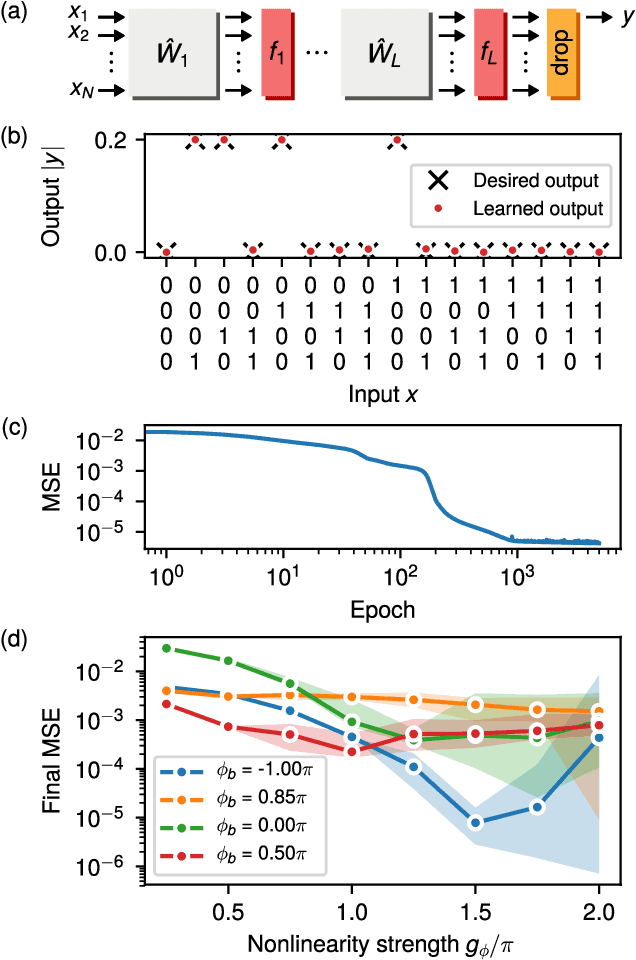
We introduce an electro-optic hardware platform for nonlinear activation functions in optical neural networks. The optical-to-optical nonlinearity operates by converting a small portion of the input optical signal into an analog electric signal, which is used to intensity-modulate the original optical signal with no reduction in operating speed. This scheme allows for complete nonlinear on-off contrast in transmission at relatively low optical power thresholds and eliminates the requirement of having additional optical sources between each layer of the network. Moreover, the activation function is reconfigurable via electrical bias, allowing it to be programmed or trained to synthesize a variety of nonlinear responses. Using numerical simulations, we demonstrate that this activation function significantly improves the expressiveness of optical neural networks, allowing them to perform well on two benchmark machine learning tasks: learning a multi-input exclusive-OR (XOR) logic function and classification of images of handwritten numbers from the MNIST dataset. The addition of the nonlinear activation function improves test accuracy on the MNIST task from 85% to 94%.

Training of photonic neural networks through in situ backpropagation

Recently, integrated optics has gained interest as a hardware platform for implementing machine learning algorithms. Of particular interest are artificial neural networks, since matrix-vector multi- plications, which are used heavily in artificial neural networks, can be done efficiently in photonic circuits. The training of an artificial neural network is a crucial step in its application. However, currently on the integrated photonics platform there is no efficient protocol for the training of these networks. In this work, we introduce a method that enables highly efficient, in situ training of a photonic neural network. We use adjoint variable methods to derive the photonic analogue of the backpropagation algorithm, which is the standard method for computing gradients of conventional neural networks. We further show how these gradients may be obtained exactly by performing intensity measurements within the device. As an application, we demonstrate the training of a numerically simulated photonic artificial neural network. Beyond the training of photonic machine learning implementations, our method may also be of broad interest to experimental sensitivity analysis of photonic systems and the optimization of reconfigurable optics platforms.