Rong-Jun Qin
NeoRL-2: Near Real-World Benchmarks for Offline Reinforcement Learning with Extended Realistic Scenarios
Mar 25, 2025
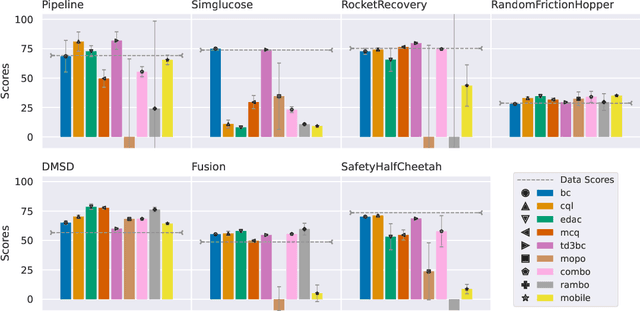
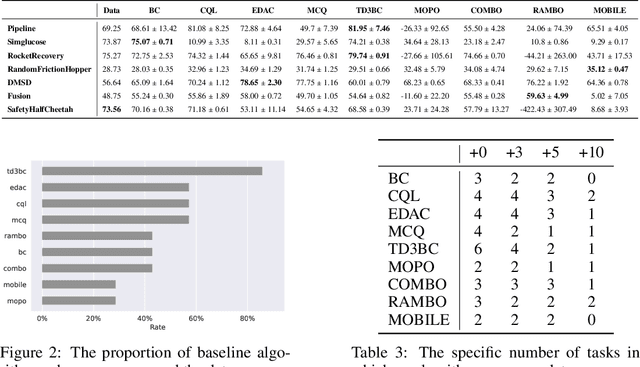
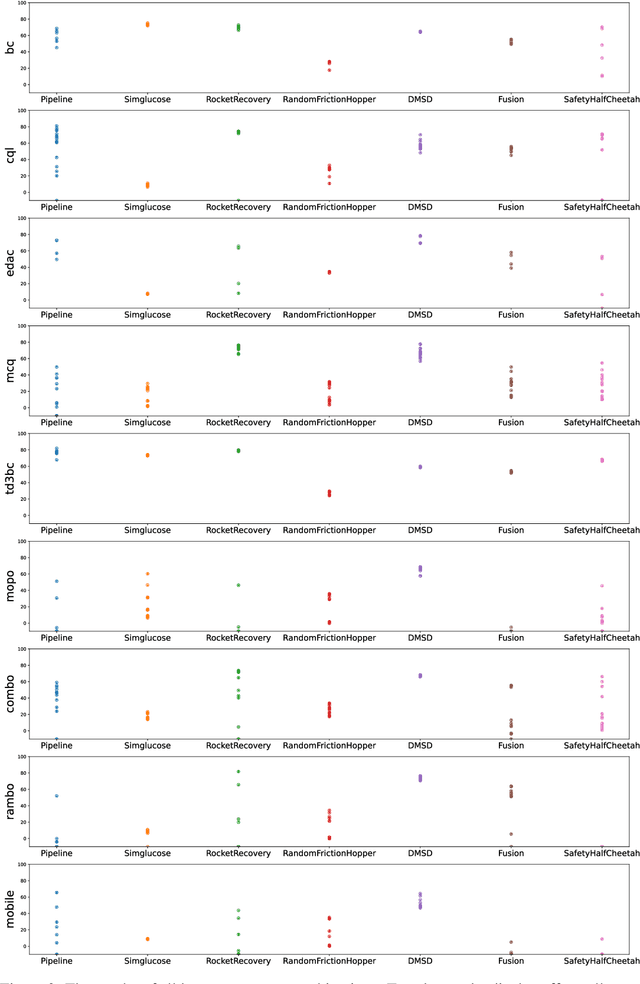
Abstract:Offline reinforcement learning (RL) aims to learn from historical data without requiring (costly) access to the environment. To facilitate offline RL research, we previously introduced NeoRL, which highlighted that datasets from real-world tasks are often conservative and limited. With years of experience applying offline RL to various domains, we have identified additional real-world challenges. These include extremely conservative data distributions produced by deployed control systems, delayed action effects caused by high-latency transitions, external factors arising from the uncontrollable variance of transitions, and global safety constraints that are difficult to evaluate during the decision-making process. These challenges are underrepresented in previous benchmarks but frequently occur in real-world tasks. To address this, we constructed the extended Near Real-World Offline RL Benchmark (NeoRL-2), which consists of 7 datasets from 7 simulated tasks along with their corresponding evaluation simulators. Benchmarking results from state-of-the-art offline RL approaches demonstrate that current methods often struggle to outperform the data-collection behavior policy, highlighting the need for more effective methods. We hope NeoRL-2 will accelerate the development of reinforcement learning algorithms for real-world applications. The benchmark project page is available at https://github.com/polixir/NeoRL2.
Scaling Multi-Objective Security Games Provably via Space Discretization Based Evolutionary Search
Mar 28, 2023Abstract:In the field of security, multi-objective security games (MOSGs) allow defenders to simultaneously protect targets from multiple heterogeneous attackers. MOSGs aim to simultaneously maximize all the heterogeneous payoffs, e.g., life, money, and crime rate, without merging heterogeneous attackers. In real-world scenarios, the number of heterogeneous attackers and targets to be protected may exceed the capability of most existing state-of-the-art methods, i.e., MOSGs are limited by the issue of scalability. To this end, this paper proposes a general framework called SDES based on many-objective evolutionary search to scale up MOSGs to large-scale targets and heterogeneous attackers. SDES consists of four consecutive key components, i.e., discretization, optimization, restoration and evaluation, and refinement. Specifically, SDES first discretizes the originally high-dimensional continuous solution space to the low-dimensional discrete one by the maximal indifference property in game theory. This property helps evolutionary algorithms (EAs) bypass the high-dimensional step function and ensure a well-convergent Pareto front. Then, a many-objective EA is used for optimization in the low-dimensional discrete solution space to obtain a well-spaced Pareto front. To evaluate solutions, SDES restores solutions back to the original space via bit-wisely optimizing a novel solution divergence. Finally, the refinement in SDES boosts the optimization performance with acceptable cost. Theoretically, we prove the optimization consistency and convergence of SDES. Experiment results show that SDES is the first linear-time MOSG algorithm for both large-scale attackers and targets. SDES is able to solve up to 20 attackers and 100 targets MOSG problems, while the state-of-the-art methods can only solve up to 8 attackers and 25 targets ones. Ablation study verifies the necessity of all components in SDES.
Unified Policy Optimization for Continuous-action Reinforcement Learning in Non-stationary Tasks and Games
Aug 19, 2022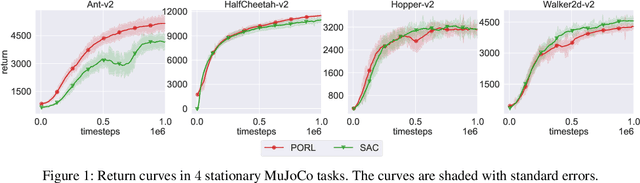

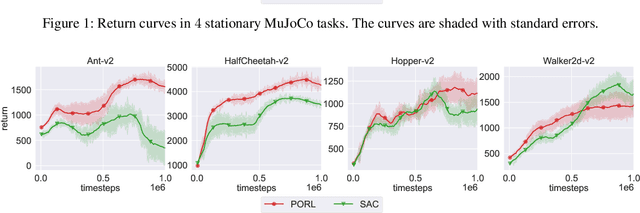

Abstract:This paper addresses policy learning in non-stationary environments and games with continuous actions. Rather than the classical reward maximization mechanism, inspired by the ideas of follow-the-regularized-leader (FTRL) and mirror descent (MD) update, we propose a no-regret style reinforcement learning algorithm PORL for continuous action tasks. We prove that PORL has a last-iterate convergence guarantee, which is important for adversarial and cooperative games. Empirical studies show that, in stationary environments such as MuJoCo locomotion controlling tasks, PORL performs equally well as, if not better than, the soft actor-critic (SAC) algorithm; in non-stationary environments including dynamical environments, adversarial training, and competitive games, PORL is superior to SAC in both a better final policy performance and a more stable training process.
Adversarial Counterfactual Environment Model Learning
Jun 10, 2022

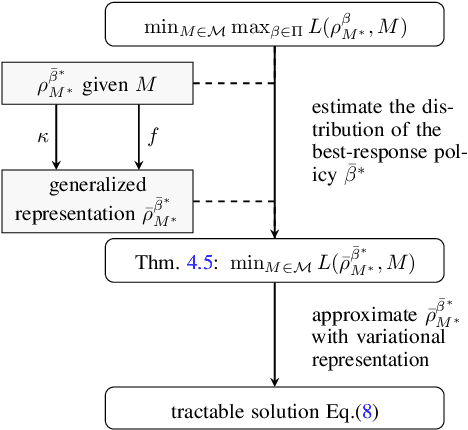

Abstract:A good model for action-effect prediction, named environment model, is important to achieve sample-efficient decision-making policy learning in many domains like robot control, recommender systems, and patients' treatment selection. We can take unlimited trials with such a model to identify the appropriate actions so that the costs of queries in the real world can be saved. It requires the model to handle unseen data correctly, also called counterfactual data. However, standard data fitting techniques do not automatically achieve such generalization ability and commonly result in unreliable models. In this work, we introduce counterfactual-query risk minimization (CQRM) in model learning for generalizing to a counterfactual dataset queried by a specific target policy. Since the target policies can be various and unknown in policy learning, we propose an adversarial CQRM objective in which the model learns on counterfactual data queried by adversarial policies, and finally derive a tractable solution GALILEO. We also discover that adversarial CQRM is closely related to the adversarial model learning, explaining the effectiveness of the latter. We apply GALILEO in synthetic tasks and a real-world application. The results show that GALILEO makes accurate predictions on counterfactual data and thus significantly improves policies in real-world testing.
Improving Fictitious Play Reinforcement Learning with Expanding Models
Nov 28, 2019

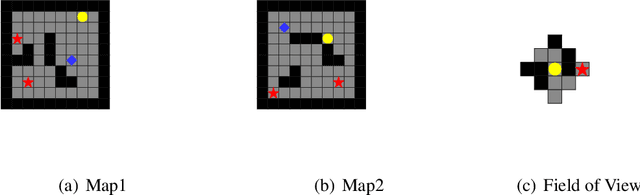
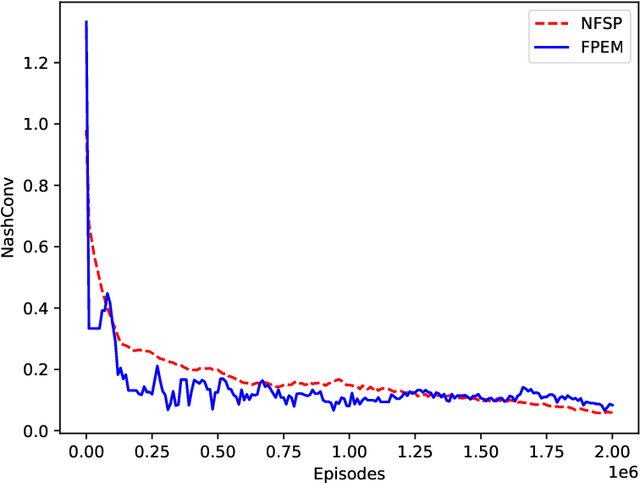
Abstract:Fictitious play with reinforcement learning is a general and effective framework for zero-sum games. However, using the current deep neural network models, the implementation of fictitious play faces crucial challenges. Neural network model training employs gradient descent approaches to update all connection weights, and thus is easy to forget the old opponents after training to beat the new opponents. Existing approaches often maintain a pool of historical policy models to avoid the forgetting. However, learning to beat a pool in stochastic games, i.e., a wide distribution over policy models, is either sample-consuming or insufficient to exploit all models with limited amount of samples. In this paper, we propose a learning process with neural fictitious play to alleviate the above issues. We train a single model as our policy model, which consists of sub-models and a selector. Everytime facing a new opponent, the model is expanded by adding a new sub-model, where only the new sub-model is updated instead of the whole model. At the same time, the selector is also updated to mix up the new sub-model with the previous ones at the state-level, so that the model is maintained as a behavior strategy instead of a wide distribution over policy models. Experiments on Kuhn poker, a grid-world Treasure Hunting game, and Mini-RTS environments show that the proposed approach alleviates the forgetting problem, and consequently improves the learning efficiency and the robustness of neural fictitious play.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge