Improving Fictitious Play Reinforcement Learning with Expanding Models
Paper and Code
Nov 28, 2019

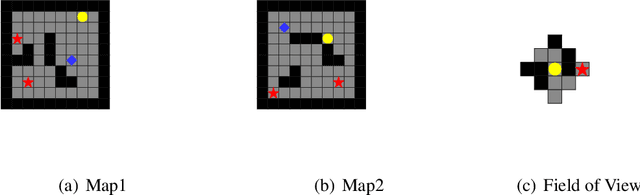
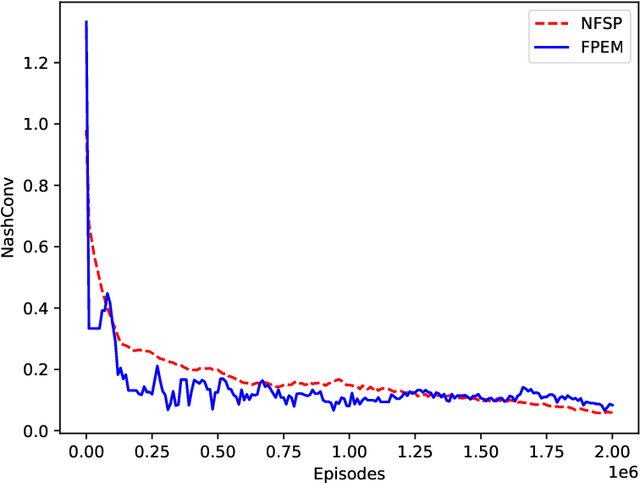
Fictitious play with reinforcement learning is a general and effective framework for zero-sum games. However, using the current deep neural network models, the implementation of fictitious play faces crucial challenges. Neural network model training employs gradient descent approaches to update all connection weights, and thus is easy to forget the old opponents after training to beat the new opponents. Existing approaches often maintain a pool of historical policy models to avoid the forgetting. However, learning to beat a pool in stochastic games, i.e., a wide distribution over policy models, is either sample-consuming or insufficient to exploit all models with limited amount of samples. In this paper, we propose a learning process with neural fictitious play to alleviate the above issues. We train a single model as our policy model, which consists of sub-models and a selector. Everytime facing a new opponent, the model is expanded by adding a new sub-model, where only the new sub-model is updated instead of the whole model. At the same time, the selector is also updated to mix up the new sub-model with the previous ones at the state-level, so that the model is maintained as a behavior strategy instead of a wide distribution over policy models. Experiments on Kuhn poker, a grid-world Treasure Hunting game, and Mini-RTS environments show that the proposed approach alleviates the forgetting problem, and consequently improves the learning efficiency and the robustness of neural fictitious play.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge